113

Л Е К Ц И И 18-20

Тема. Функции Грина. Основные свойства гармонических функций. Решение задачи Дирихле при помощи функции Грина. Функция Грина для сферы. Функция Грина для круга.

В математической физике часто рассматривается величина, которая зависит не только от положения точки , то есть от ее n (часто n = 1, 2, 3) пространственных координат, но и еще от какой-либо переменной, в большинстве случаев от времени t. Если рассматриваемая величина является числом, то принято говорить, что речь идет о скалярной функции точки; если же рассматриваемая величина – вектор, то говорят о векторной функции точки.

Например, плотность заряда в различных точках изолированного наэлектризованного тела представляет собой скалярную функцию точки; электрическое поле, которое создается этими зарядами в различных точках тела, представляет собой векторную функцию точки.

Вместо терминов «числовая функция точки», «вектор функция точки» употребляются равнозначные: скалярное поле, векторное поле.

Скалярным полем называется область плоскости, каждой точке которой сопоставляется некоторое значение скалярной величины.

Так как произвольная точка на плоскости характеризуется координатами x, y или радиусвектором , то аналитически любое скалярное поле может быть задано либо в виде функции координат , либо в функции радиусвектора . Геометрически двумерное скалярное поле можно рассматривать как некоторую поверхность в пространстве трех измерений, где всякой точке ( x, y) плоскости соответствует своя высота .

Пусть является в заданной области непрерывной, однозначной и дифференцируемой функцией координат. Возьмем определенную точку и проведем через нее прямую по некоторому направлению (l). Рассмотрим значение функции (M) в самой точке M и в близкой к ней точке отстоящей от M на расстоянии l вдоль выбранного направления l. Предел отношения

,

если он существует, называется производной от функции (M) по направлению (l). Эта производная характеризует быстроту изменения функции (M) в точке M в направлении (l).

Функция (M) имеет в каждой точке бесчисленное множество производных, но нетрудно показать, что производная по любому направлению выражается через производные по трем взаимно перпендикулярным направлениям X, Y, Z по формуле:

.

Введем в рассмотрение поверхности уровня скалярного поля. Эти поверхности характеризуются условием, что во всех точках такой поверхности функция  сохраняет одно и то же постоянное значение. Придавая этой постоянной различные численные значения, получим семейство поверхностей уровня. Будем считать, что через каждую точку M некоторой области проходит гладкая поверхность уровня (например S).

Если , где , есть непрерывно дифференцируемое скалярное поле, то градиентом его называется вектор

grad u

или, короче, grad u = u, где . Градиент поля u в данной точке (x, y, z) направлен по нормали к поверхности уровня u(x, y, z) = C, проходящей через эту точку. Этот вектор для каждой точки поля по величине

и направлению по нормали дает наибольшую скорость изменения функции u.

Если каждой точке некоторой части плоскости сопоставляется определенная векторная величина , то говорят, что задано векторное поле или .

Заметим, что поскольку вектор в пространстве определяется тремя скалярными проекциями , и , то задание векторного поля эквивалентно заданию трех скалярных полей , и .

Если есть непрерывно дифференцируемое векторное поле, то скаляр

называется дивергенцией этого поля.

Если n – любое направление в пространстве , то проекция вектора a(r) на это направление будет

.

Выделим в векторном поле некоторый объем V и пусть S есть поверхность, ограничивающая этот объем, а n – направление нормали к S, внешней по отношению к объему V. Применим формулу Остроградского к функциям , и , считая, что эти функции непрерывны и имеют непрерывные частные производные первого порядка в области V вплоть до ее границы:

таким образом, формулу Остроградского можно записать так:

div a dv =

При изучении уравнений эллиптического типа мы часто будем пользоваться формулами Грина, являющимися прямым следствием формулы Остроградского.

Формулу Остроградского обычно записывают в виде

,

где T – некоторый объем, ограниченный достаточно гладкой поверхностью , - элемент объема, - углы внешней нормали n к поверхности  с координатными осями, P, Q, R - произвольные дифференцируемые функции.

Если P, Q, R рассматривать как компоненты некоторого вектора , то формулу Остроградского можно записать следующим образом:

,

где

div A = , .

Пусть и - функции, непрерывные вместе со своими первыми производными внутри и имеющие непрерывные вторые производные внутри T. Рассмотрим интеграл

.

Применяя очевидное тождество

и два аналогичных для и , можем переписать интеграл в виде

.

Преобразуя первое из слагаемых в правой части по формулу Остроградского

,

или

.

Таким образом, мы получим первую формулу Грина:

= . (1)

Левая часть этого равенства не меняется при перестановке функций u и v, а потому то же относится и к правой части, то есть, мы можем написать

= ,

откуда и получается вторая формула Грина:

. (2)

Следствием формулы Грина является важная в приложениях формула, дающая значение функции в любой точке внутри T в виде суммы некоторого поверхностного и некоторого объемного интеграла.

Пусть U(M) – функция, непрерывная вместе с первыми производными в области D + S и имеющая вторые производные в области D вплоть до S. Рассмотрим функцию , где - некоторая внутренняя точка области D, а R – расстояние от до переменной точки M в области D. Поскольку эта функция имеет внутри D разрыв непрерывности в точке , то непосредственно применить вторую формулу Грина в области D к функциям u и v нельзя. Выделим из этого тела малую сферу с центром и малым радиусом  и обозначим через оставшуюся часть тела D и через - поверхность выделенной сферы. В области функции U и V обладают требуемым свойством непрерывности, и, применяя к этой области вторую формулу Грина, мы получим:

,

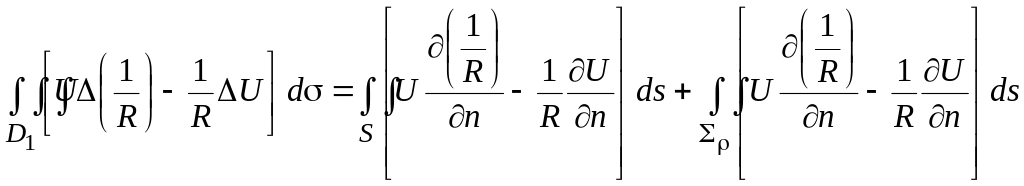причем интегрирование совершается по обеим поверхностям S и , ограничивающим тело . Но, функция удовлетворяет уравнению Лапласа, то есть, . Кроме того, на сфере нормаль (n) направлена внутрь сферы прямо противоположна направлению радиуса R, так что производная по нормали под знаком интеграла по есть взятая с обратным знаком производная по R. Принимая во внимание все сказанное, мы можем переписать формулу (1) в виде:

.

Будем теперь стремить радиус  выделенной сферы у нулю. При этом первое из слагаемых в написанной формуле будет стремиться к объемному интегралу по всему телу D. Второе слагаемое от  не зависит. Покажем, что третье из написанных слагаемых стремится к пределу . Принимая во внимание, что на величина R имеет постоянное значение , можем написать:

.

Применяя теорему о среднем, будем иметь:

,

где  некоторая точка на поверхности сферы . Эта точка стремится к при   0. Откуда видно, что написанное выше выражение стремится к . Применяя теорему о среднем к последнему слагаемому, получим

.

Производные первого порядка функции U по любому направлению при стремлении к остаются ограниченными, так как по предположению функция U везде внутри D имеет непрерывные производные до второго порядка. Множитель 4 стремится к нулю при   0. Отсюда видно, что последнее слагаемое в формуле (2) стремится к нулю. Окончательно формула (2) в пределе основную интегральную формулу Грина:

. (3)