
- •Лекция 10 . Плоскость в пространстве
- •10.1. Плоскость в пространстве
- •10.2. Общее уравнение плоскости и его исследование
- •10.3. Уравнение плоскости в отрезках
- •10.4. Уравнение плоскости, проходящее через три заданные точки
- •10.5. Условия параллельности и перпендикулярности двух плоскостей
- •11.3. Направляющий вектор прямой
- •11.4. Приведение общего уравнения прямой в пространстве к каноническому виду
- •11.5. Параметрическое уравнение прямой
- •12. Поверхности второго порядка
- •12.1 Эллипсоид
- •12.2 Гиперболоид
- •Однополостный гиперболоид
- •12.3 Параболоид Эллиптический параболоид
- •Гиперболический параболоид
- •12.4 Конус
- •Обобщённая таблица по теме: «Плоскость. Прямая в пространстве»
Лекция 10 . Плоскость в пространстве
10.1. Плоскость в пространстве
Определение 10.10. Плоскостью называется геометрическое место точек, координаты которых удовлетворяют уравнению:
![]() (10.1)
(10.1)
Если левая часть (10.1) есть многочлен, то плоскость называется алгебраической, степень этого многочлена должна быть единицей, т.к. плоскость – это поверхность первого порядка.
Пусть
в декартовой системе координат дана
некоторая плоскость ,
точка
![]() .
.
Определение
10.2. Любой
вектор
![]() ,
перпендикулярный плоскости ,
будем называть нормальным вектором
этой плоскости -
,
перпендикулярный плоскости ,
будем называть нормальным вектором
этой плоскости -
![]() .
.
П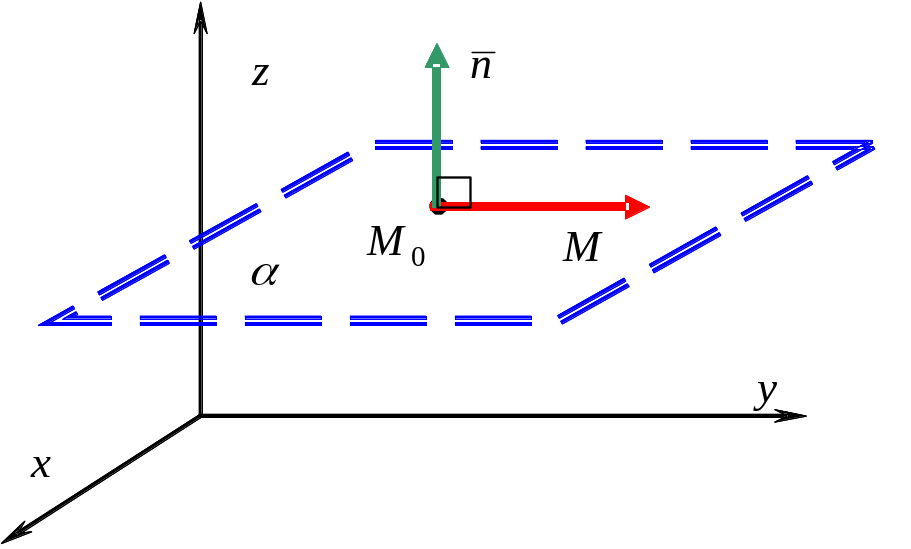 усть
усть
![]() - произвольная точка пространства.
Рассмотрим вектор
- произвольная точка пространства.
Рассмотрим вектор
![]() .
Если точка
.
Если точка
![]() ,
то
,
то
![]() .
Если точка
.
Если точка
![]() ,
то эти векторы не перпендикулярны. Таким
образом, условием принадлежности точки
М
к плоскости
является условие,
,
т.е.
,
то эти векторы не перпендикулярны. Таким
образом, условием принадлежности точки
М
к плоскости
является условие,
,
т.е.
![]() .
(10.2)
.
(10.2)
Это и есть уравнение плоскости. Распишем его в координатах. Т.к.
![]()
![]() (10.3)
(10.3)
Это
уравнение плоскости, проходящее через
точку
![]() и перпендикулярно вектору
и перпендикулярно вектору
![]() где
где
![]() ,
,
![]() - координаты точки
известной точки,
- координаты точки
известной точки,
![]() - координаты точки М
– текущей точки плоскости.
- координаты точки М
– текущей точки плоскости.
Пример
10.1.
![]() .
Написать уравнение плоскости
.
Написать уравнение плоскости
![]() ;
;
![]() - уравнение
плоскости.
- уравнение
плоскости.
Раскроем скобки в уравнении (10.3), получим:
![]() - общее
уравнение плоскости, (10.4),
- общее
уравнение плоскости, (10.4),
где
![]() .
.
10.2. Общее уравнение плоскости и его исследование
Рассмотрим уравнение (10.4) ,
,
![]() - текущие координаты.
- текущие координаты.
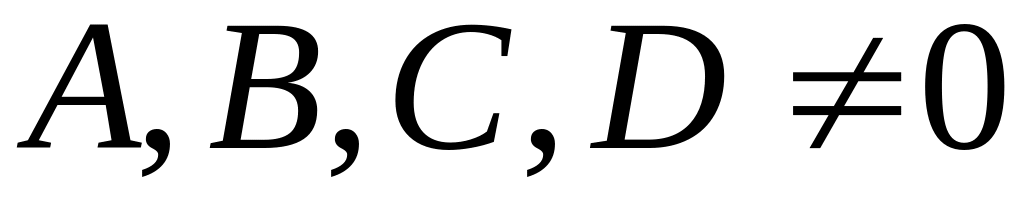
не перпендикулярен
ни одной из осей координат, т.к
не перпендикулярен
ни одной из осей координат, т.к
 не удовлетворяют уравнению (10.4), то
плоскость
не проходит через начало координат.
не удовлетворяют уравнению (10.4), то
плоскость
не проходит через начало координат.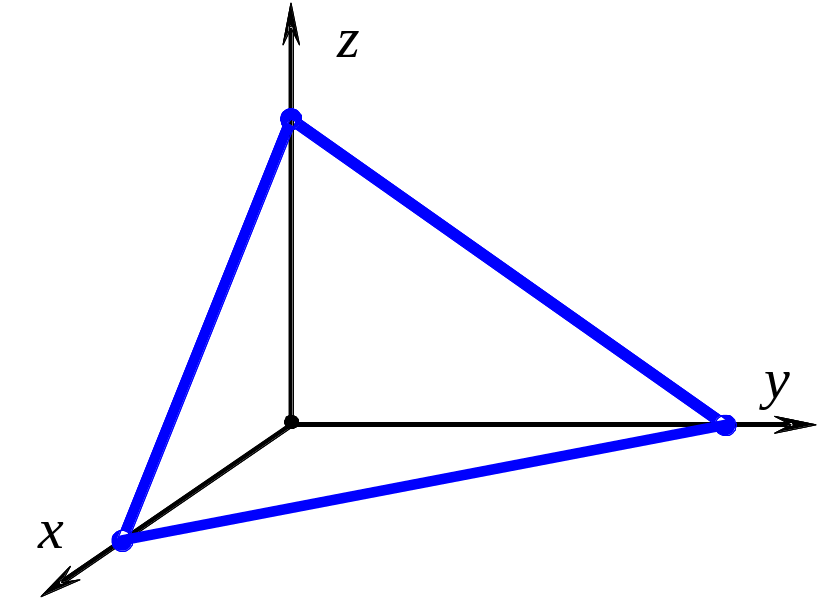
2)
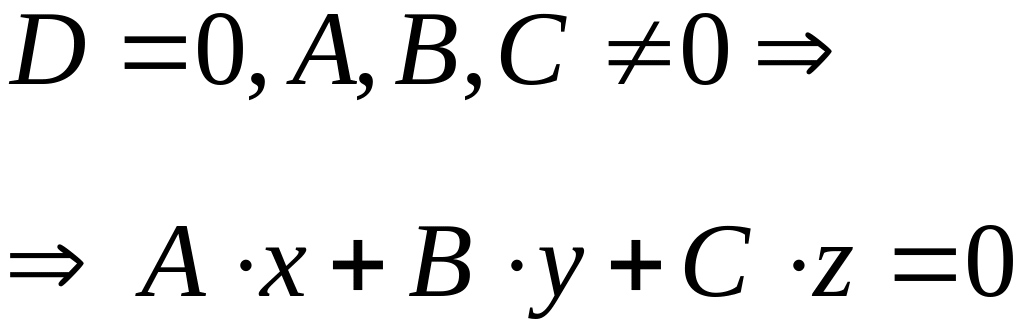 вектор
не перпендикулярен ни одной из осей
координат и значит, плоскость не
параллельна ни одной из осей координат,
т.к.
,
то плоскость
проходит через начало координат.
вектор
не перпендикулярен ни одной из осей
координат и значит, плоскость не
параллельна ни одной из осей координат,
т.к.
,
то плоскость
проходит через начало координат.
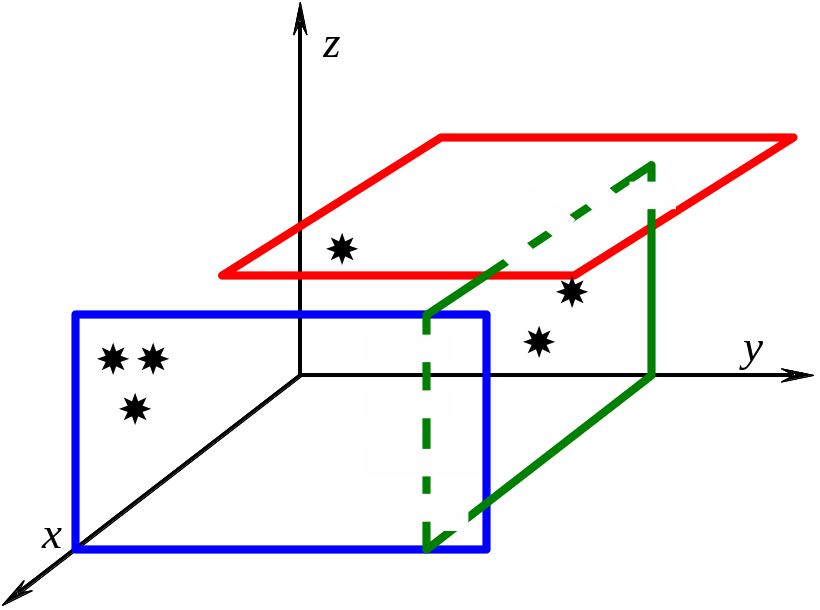
3)
![]() ,
,
а
плоскость
![]() .
Если:
.
Если:
![]() ,
то содержит ось
,
то содержит ось
![]() .
.
4)![]() ,
то плоскость параллельна Оу,
при
,
то плоскость параллельна Оу,
при
![]() плоскость содержит ось Оу.
плоскость содержит ось Оу.
5)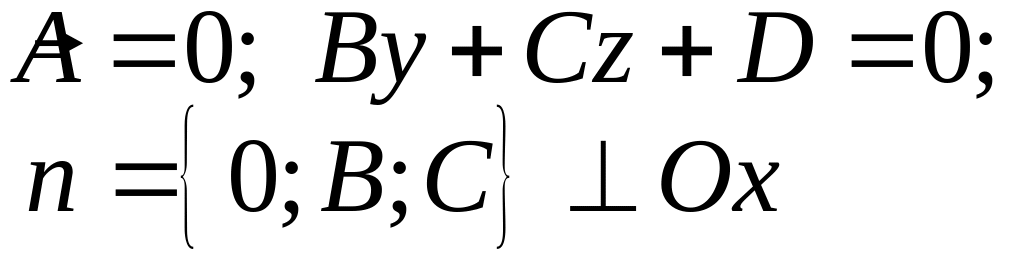 ,
то плоскость параллельна оси
,
то плоскость параллельна оси
![]() ,
,
то плоскость содержит ось
.
,
,
то плоскость содержит ось
.
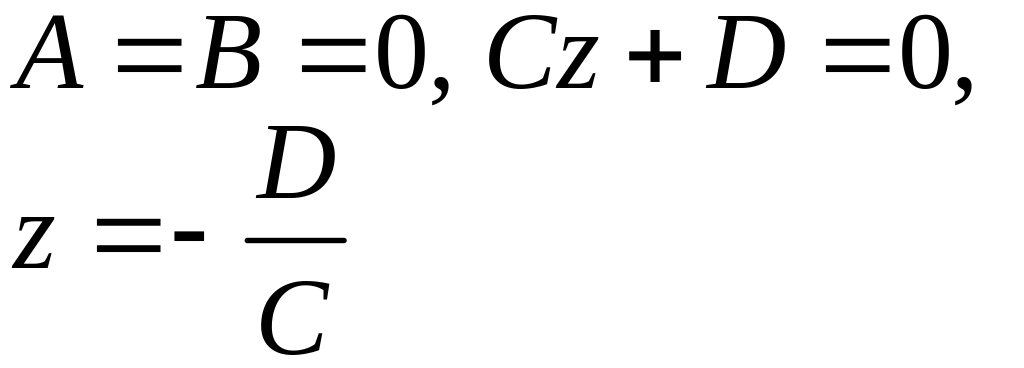 ()
()А=С=0, Ву+D=0,
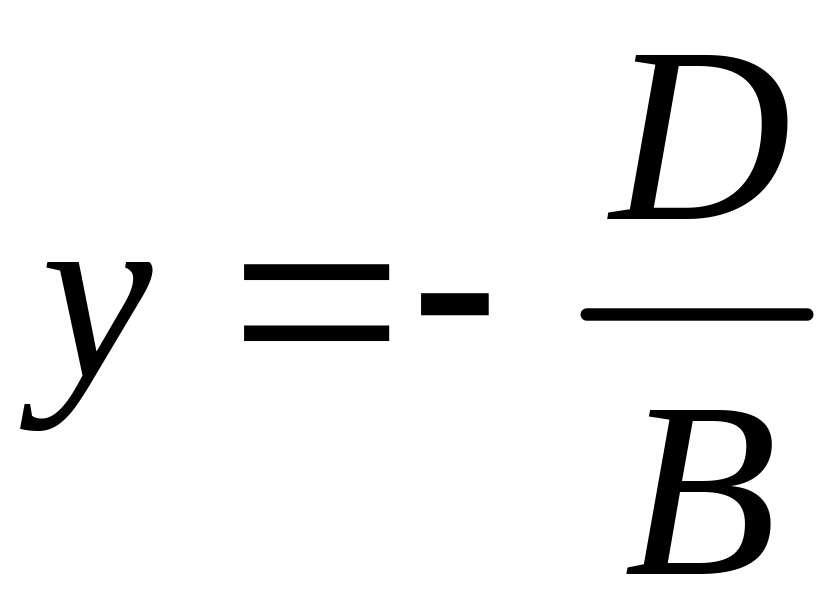 ()
()В=С=0, Ах+D=0,
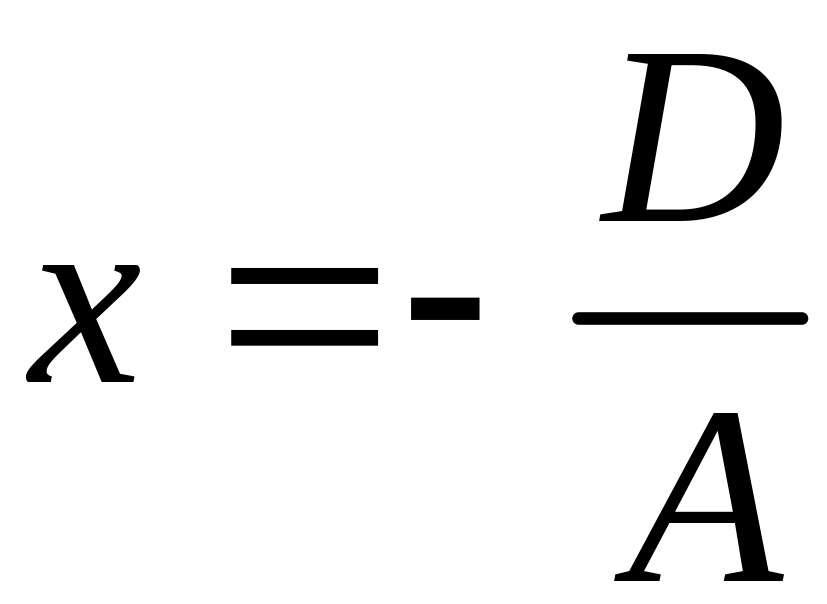 ()
()А=В=С=0 D=0; при
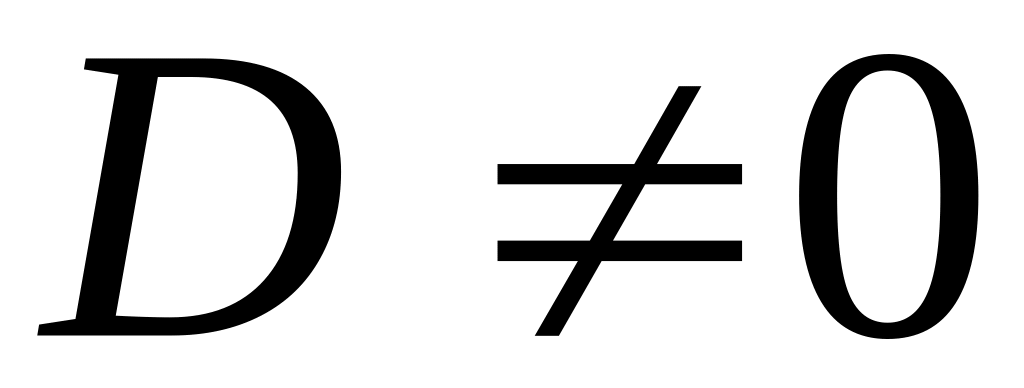 ,
уравнение теряет смысл; при
,
уравнение плоскость не определяет.
,
уравнение теряет смысл; при
,
уравнение плоскость не определяет.
10.3. Уравнение плоскости в отрезках
Пусть
плоскость
не параллельна ни одной из осей и не
проходит через точку
![]() .
Тогда она задается общим уравнением
(10.4):
.
Тогда она задается общим уравнением
(10.4):![]() ,
где
.
Пусть плоскость пересекает оси координат
в точках
,
где
.
Пусть плоскость пересекает оси координат
в точках
![]() .
.
Т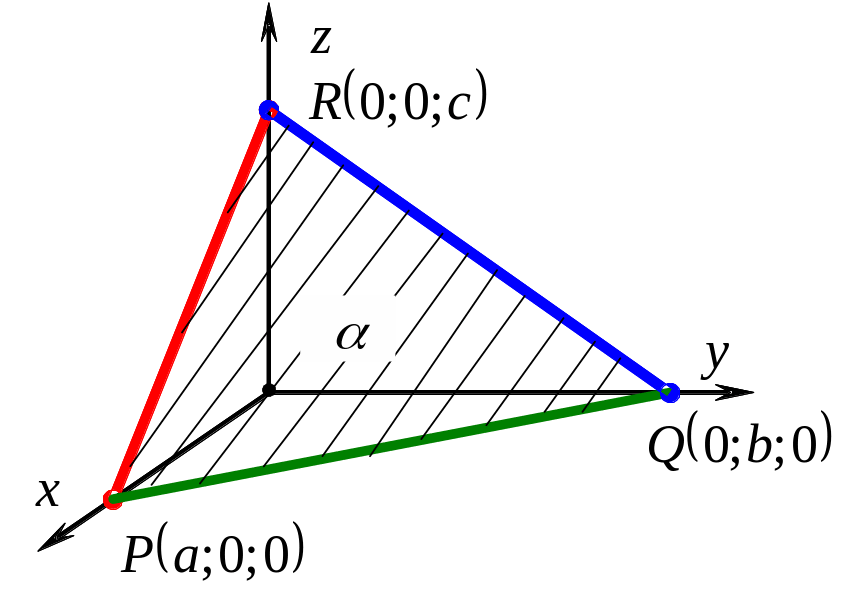 .к.
.к.
![]() ,
то её координаты удовлетворяют уравнению
плоскости:
,
то её координаты удовлетворяют уравнению
плоскости:
Для
Р:
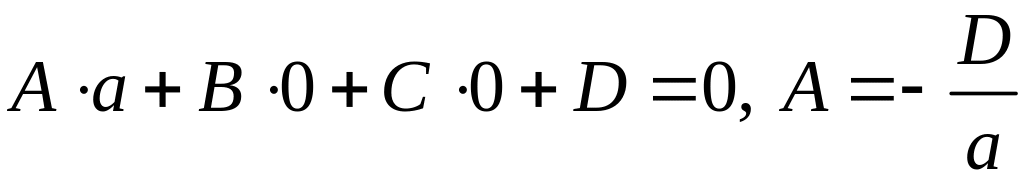 ,
,
Для
Q:
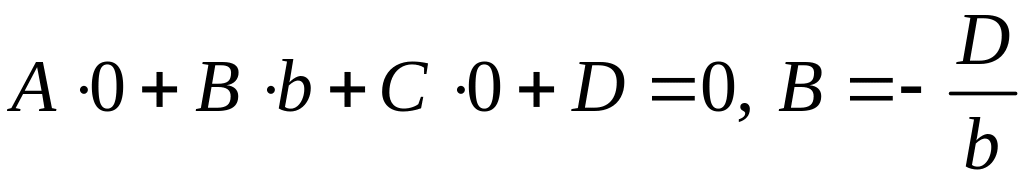 ,
,
Для
R:
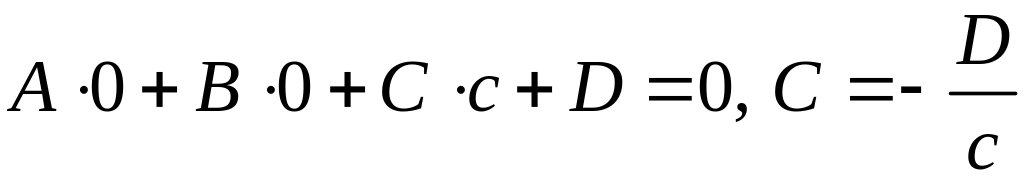 .
.
Подставляя
![]() в уравнение плоскости и разделив на
«–D»
получим:
в уравнение плоскости и разделив на
«–D»
получим:
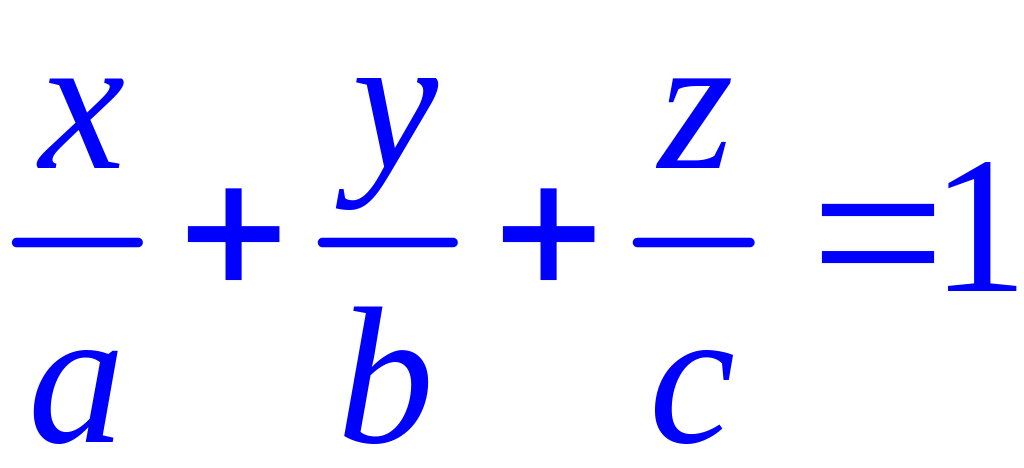 - уравнение
плоскости в отрезках (10.5)
- уравнение
плоскости в отрезках (10.5)
10.4. Уравнение плоскости, проходящее через три заданные точки
Пусть
плоскость
проходит через три заданные точки:
![]() .
Пусть
- произвольная точка пространства R3.
.
Пусть
- произвольная точка пространства R3.
Р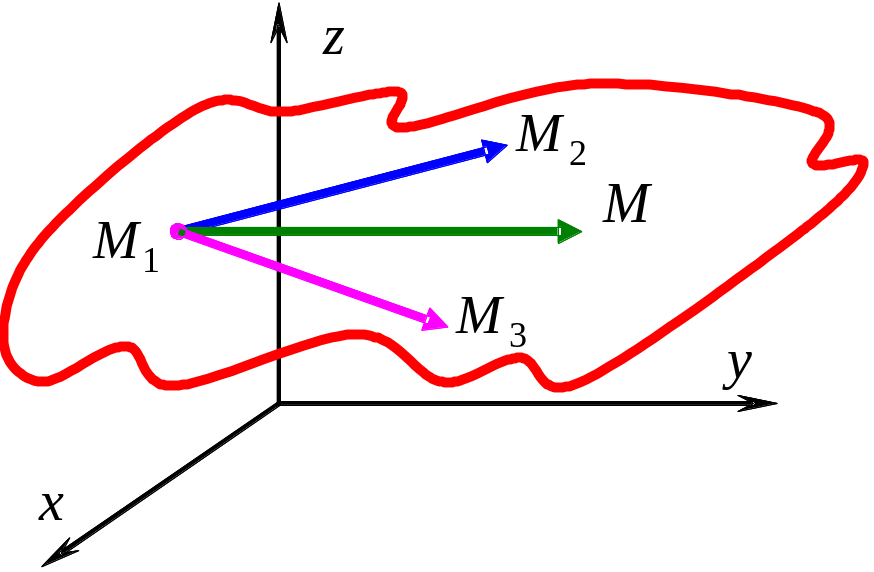 ассмотрим
три вектора:
ассмотрим
три вектора:
![]() ;
;
![]() ;
;
![]() ;
;
точка
,
вектора лежат в одной плоскости, т.е.
компланарны. По условию компланарности
трёх векторов – их смешанное произведение
равно нулю:
![]() .
.
Или
через координаты:
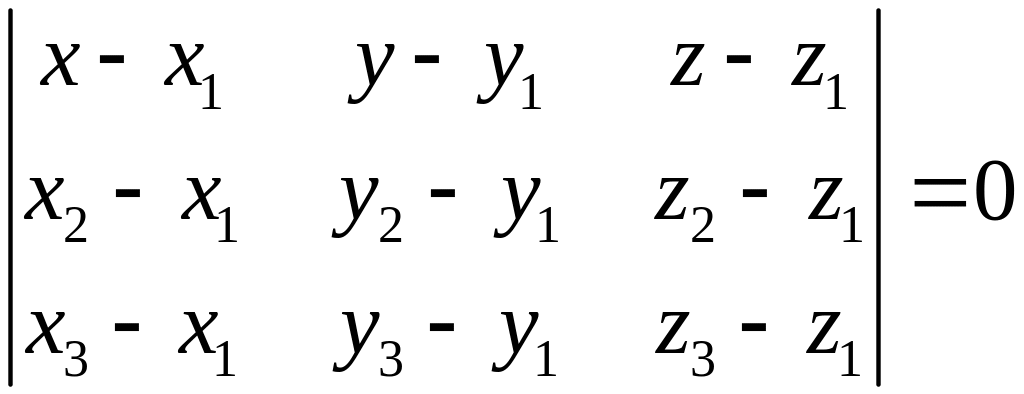 (10.6)
(10.6)
Это уравнение плоскости, проходящее через три точки.
Пример
10.2. Написать
уравнение плоскости, проходящее через
точки
![]() .
.
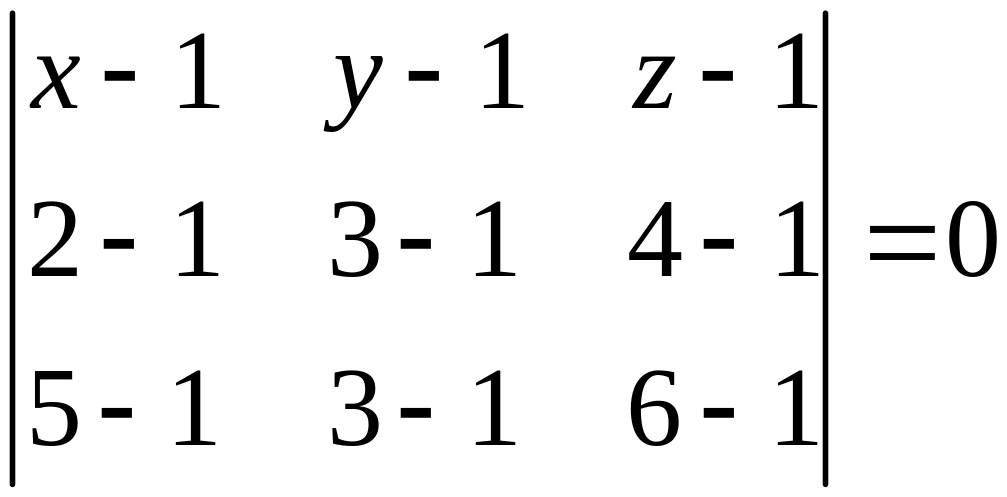 ;
;
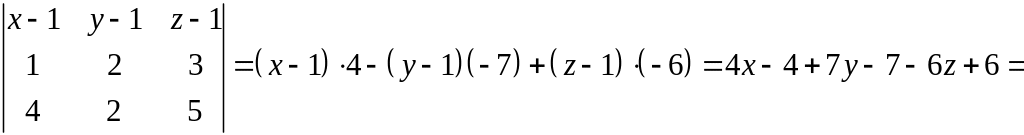
![]() - уравнение
плоскости.
- уравнение
плоскости.
