3. Модем с квадратурно-амплитудной модуляцией кам-16

При квадратурно-амплитудной модуляции (КАМ) изменяются как фаза, так и амплитуда сигнала, что позволяет увеличить количество бит, передаваемых одним сигналом.

Пользуясь геометрической трактовкой, каждый сигнал КАМ можно представить вектором в сигнальном пространстве. Отмечая только концы векторов, получаем сигнальное созвездие, в котором каждая точка имеет координаты, определяемые значениями координат x и y в формуле (4).

Рассмотрим вариант модулятора, когда координаты векторов x и y принимают значения: +1, -1, +3, -3. В табл. 5 представлены варианты передаваемых кодов и соответствующие им сигналы. Каждый сигнал передает 4 бита информации. Сигнальное созвездие показано на рис.4.

Таблица 5

Код	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
x	1	1	1	1	3	3	3	3	-1	-1	-1	-1	-3	-3	-3	-3
y	1	3	-1	-3	1	3	-1	-3	1	3	-1	-3	1	3	-1	-3

И з теории связи известно, что при равном числе точек в сигнальном созвездии спектр сигналов КАМ идентичен спектру сигналов ФМ. Однако помехоустойчивость систем КАМ и ФМ различна.

При равном числе сигнальных векторов сигналы системы КАМ имеют лучшие характеристики. Основная причина этого состоит в том, что расстояние между соседними сигнальными точками в системе ФМ (при равной средней энергии сигналов) меньше расстояния между сигнальными точками в системе КАМ.

Расстояние между соседними сигнальными точками (при большом числе точек) в системе с ФМ равно приблизительно синусу угла между векторами:

d₁  sin (2/m), (7)

где m – число сигнальных точек.

Для системы КАМ, имеющей такое же количество сигнальных точек, расстояние между соседними точками:

d₂  2/(L-1), (8)

где L – число уровней сигнала по любой из координат( m = L*L ).

При выводе формул (7), (8) полагаем, что радиус окружности равен 1.

y (S)

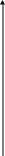
  - 3  

1101 1001 0001 0101

2

1100 1000 0000 0100

  - 1  

x (C)

-3 -2 -1 1 2 3

  - -1  

1110 1010 0010 0110

-2

1111 1011 0011 0111

  - -3  

Рис.4. Сигнальное созвездие КАМ-16

Например, при m = 16 и L = 4 получим:

d₁ = 0,396, d₂ = 0,47.

Алгоритм работы демодулятора поясняет рис.4. Сигнальная плоскость разделена осями координат а также вертикальными и горизонтальными линиями, проходящими через точки с координатами +2, -2 , на 16 зон. Каждая зона соответствует одному коду из ансамбля на передающей стороне.

Демодуляция сигналов может быть выполнена по алгоритму, включающему следующие шаги:

1. Вычисление составляющих S и C сигнала по формулам (4), (5).

2. Сравнение составляющей S с порогами –2, 0, +2 и определение горизонтальной зоны, в которую попал вектор принятого сигнала. В результате будут получены два младших (правых) разряда кода.

3. Сравнение составляющей С с порогами –2, 0, +2 и определение вертикальной зоны, в которую попал вектор принятого сигнала. В результате будут получены два старших разряда кода.

Ошибка приема будет в том случае, когда сигнальный вектор, соответствующий некоторому коду, исказится в канале под воздействием помехи и попадет после обработки в зону другого кода.

С целью уменьшения влияния помехи на число ошибок в демодуляторе следует так распределить коды между векторами, чтобы переход в соседнюю зону не приводил бы к появлению более одного ошибочного разряда. Это требование к оптимальному размещению кодов на сигнальной плоскости выполнено в примере.