1.1. Первообразная и неопределенный интеграл

 Интегральное исчисление решает обратную задачу по отношению к дифференциальному исчслению: по данному дифференциалу, а следовательно, и производной неизвестной функции F(x), требуется определить эту функцию.

         Пусть известна функция f(x) и нужно по данной функции  определить F(x) таким образом, чтобы

dF(x) = f(x)dx

или соответственно                       .                                      (1.1)

Для простоты будем предполагать, что равенство (1.1) выполнено на некотором промежутке  (конечном или бесконечном).

 Определение 1.1.  Пусть функция f определена на некотором промежутке, т.е. на отрезке, интервале или полуинтервале числовой оси. Функция F, определенная на этом же промежутке  называется первообразной функции f , если выполнено (1.1) для каждого х из указанного промежутка.

 

         Очевидно, что если F является первообразной для f на  <a,b>, то функция F+ C  (C-Const ), также является первообразной для f на <a,b>.

         Действительно,

                                      [F(x) + C]' = F'(x) = f(x), х <a,b>.                           (1.2)

 ф

1.1.2. Неопределенный интеграл

        В дальнейшем мы будем предполагать, если явно не оговорено противное, что рассматриваемая функция f(х) определена и непрерывна на некотором конечном или бесконечном промежутке <a,b>.

         Введем теперь основное понятие интегрального исчисления - понятие неопределенного интеграла.

 Определение 1.2. Совокупность всех первообразных функции f, определенных на некотором промежутке <a,b>, называется неопределенным интегралом от функции f на этом промежутке и обозначается

                                                                   .                                                            

 - называется функцией общего вида, дифференциал которой равен подынтегральному выражению f(x)dx, и, следовательно, производная по переменной х равна подынтегральной функции f(x) во всех точках <a,b>.

  Геометрически неопределенный интеграл

y = F(x) + C

  представляет собой семейство “параллельных” к ривых.

 

 

 

 

Рис. 3.2

 Метод замены переменной

Основные понятия и теоремы

Т е о р е м а 2 . Пусть функция x = ϕ(t) определена и дифференцируема на промежутке T,

а промежутокTX − множество ее значений. Пусть функция y = f(x) определена на X и

имеет на этом промежутке первообразную F(x).

Тогда на промежутке TT функция F(ϕ(t)) является первообразной для функции f(ϕ(t))ϕ /(t).

Из теоремы 2 следует, что

∫ f(ϕ(t))ϕ/(t) dt = F(ϕ(t)) + C, (1) а так как F(ϕ(t)) + C = (F(x) + C)|x = ϕ(t) = ∫ f(x) dx|x = ϕ(t)

, то равенство (1) можно записать ввиде ∫ f(x) dx|x = ϕ( )t = ∫ f(ϕ(t))ϕ'(t) dt. (2)

Равенство (2) называется формулой замены переменной в неопределенном интеграле.

Если функция x = ϕ(t) имеет обратную функцию t = ϕ −1 (x) то из равенства (2) следует

∫ f(x) dx = ∫ f(ϕ(t))ϕ/(t) dt|t = ϕ−1( )x . (3)

Эта формула является основной рабочей формулой при вычислении интеграла ∫ f(x) dx

1.1.3. Основные свойства неопределенного интеграла

        

Основываясь на формуле (2.2), выведем основные свойства.

     1. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции.

,

                                                                  .                                                        (1.5)

         2. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции  равен самой этой функции с точностью до постоянного слагаемого.

В самом деле, пусть

,

где ^/(х) - непрерывна. Тогда (х) очевидно является первообразной для ^/(х). Поэтому

.

Замечание. В формулах (1.4) и (1.5) знаки   и d, следующие друг за другом в том или ином порядке, взаимно уничтожают друг друга, если не считать константы.

(то есть интегрирование и дифференцирование являются взаимно обратными математическими операциями).

 

         3. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла.

Ecли k = const, тогда

                                               .

Д о к а з а т е л ь с т в о:   Пусть f(x) имеет первообразную F(x)+C.

Рассмотрим kF(x)+kC - первообразная, тогда kF(x)+kC^/= kF^/(x)+0=kf(x), так как F^/(x)=f(x) с точностью до константы.

      4. (Аддитивность интеграла относительно функций). Неопределенный  интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме неопределенных интегралов от этих функций.

         Пусть

, ,  и, следовательно,

 ,  , .

         Положим F=F₁+F₂-F₃, тогда

, то есть F является первообразной для f₁ + f₂ - f₃, поэтому

.

 

 

.

 

в) Метод интегрирования по частям

  Пусть u и v - непрерывно дифференцируемые функции от х.

   d(uv) = udv + vdu.

Отсюда

udv=d(uv)-vdu.

 Интегрируя обе части этого уравнения, получим

 

или

                                              .                                      

Пример.

                   1. .

                   2.  .

Интегрирование простейших рациональных дробей.

Если P(z) и Q(z) – многочлены в комплексной области, то   - рациональная дробь. Она называется правильной, если степень P(z) меньше степениQ(z), и неправильной, если степень Р не меньше степени Q.

Любую неправильную дробь можно представить в виде:     ,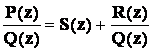

где

P(z) = Q(z) S(z) + R(z) a R(z) – многочлен, степень которого меньше степени Q(z).

Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как   является правильной дробью.

 

         Определение 5. Простейшими (или элементарными) дробями называются дроби следующих видов:

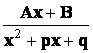1)  ,      2)  ,    3)  ,     4)           .

 

Выясним, каким образом они интегрируются.

1)   

2)    

3)     .

 

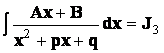         Теорема 5. Всякую правильную дробь можно представить  в виде суммы простейших дробей (без доказательства).

 

         Следствие 1. Если   - правильная рациональная дробь, и если среди корней многочлена   будут только простые действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го типа:

2.5. Интегрирование тригонометрических функций

1. Универсальная замена

          Рассмотрим интеграл вида

                                                     .                                       (2.11)

 Подстановка 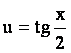  сводит интеграл  (3.1) к интегралу от рациональной дроби.

,

,

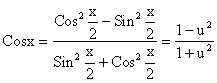то есть   х = 2arctgu,  ,

поэтому

                                .                         (2.11^\)

Пример.