
Теория графов.
Спроектировать сеть и найти максимальный поток, которая обслуживает пять микрорайонов. Расстояния между макрорайонами приведены ниже:
-
Район
a
b
c
d
e
a
15
12
10
13
b
15
4
12
8
c
12
4
8
7
d
10
12
8
5
e
13
8
7
5
Найти максимальный поток из A в E.
Решение

С помощью алгоритма Форда-Фалкерсона найдем наибольший поток из
A в C.
Шаг 1. Выбираем произвольный поток, a→e = 13.
Шаг 2. Выбираем произвольный поток, a→b→c→d→e = 4.
Шаг 3. Выбираем произвольный поток, a→b→d→e = 1.
Шаг 4. Выбираем произвольный поток, a→b→e = 8.
Шаг 5. Выбираем произвольный поток, a→c→e = 7.
Больше путей нет. Суммарный поток 13 + 4 + 1 + 8 + 7 = 33
Ответ: Максимальный поток равен 33
Система массового обслуживания
В парикмахерской работает только один мужской мастер. Среднее время стрижки одного клиента составляет 20 мин. Клиенты в среднем приходят каждые 30 мин. Все потоки в системе простейшие.
Определите вероятность простоя мастера, среднее число клиентов в очереди, среднее время ожидания в очереди, среднее время пребывания клиентов в парикмахерской.
Тоб = 20мин – время стрижки одного клиента
Тз = 30мин – время прибытия клиента
 - интенсивность
обслуживания клиентов
- интенсивность
обслуживания клиентов
Решение
1)Вероятность простоя мастера равна:
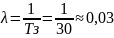 - нашел
интенсивность поступления заявки
- нашел
интенсивность поступления заявки
 - наше
интенсивность
погрешности
- наше
интенсивность
погрешности
 - вероятность
простоя мастера (0,4*100%)
40% свободен
- вероятность
простоя мастера (0,4*100%)
40% свободен
Рзан=1 - Р0 = 0,6 (0,6*100%) 60% занят
2)Средние число клиентов в очереди
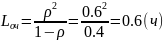 -
длина очереди
-
длина очереди
3)Среднее время ожидания в очереди
 (мин) -
среднее время ожидания
(мин) -
среднее время ожидания
4)Среднее время прибытия клиентов в парикмахерскую
 (мин)–
среднее время прибытия
(мин)–
среднее время прибытия
Теория игр.
Матричная игра задана следующей матрицей:
L
=

Найти решение матричной игры, а именно:
найти верхнюю цену игры;
нижнюю цену игры;
чистую цену игры;
указать оптимальные стратегии игроков;
привести графическое решение (геометрическую интерпретацию).
Решение
L =
Определим нижнюю и верхнюю цены игры.
Выпишем для каждой строки справа от матрицы
 ,
а снизу
,
а снизу
 каждого столбца. Тогда получим:
каждого столбца. Тогда получим:


1)Верхняя цена игры равняется 3
2)Нижняя цена игры равняется 4
Чтобы
найти чистую цену игры нам нужно сократить
матрицу:
столбец 1 доминирует над всеми столбцами, удаляем его

 строка
3 доминирует над строкой 1, удаляем строку
1
строка
3 доминирует над строкой 1, удаляем строку
1
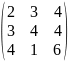 строка
3 доминирует над строкой 1, удаляем строку
1
строка
3 доминирует над строкой 1, удаляем строку
1
 столбец
3 доминирует над столбцом 1, удаляем
столбец 3
столбец
3 доминирует над столбцом 1, удаляем
столбец 3
 получаем 2х мерную
матрицу
получаем 2х мерную
матрицу
Находим стратегии играков

Стратегии игрока Х
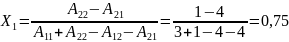

Х(0,75;0,25)

Находим чистую цену игры
3)
Стратегии игрока У
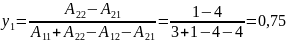

У(0,75;0,25)
 Графический
метод.
Графический
метод.

Стратегии игрока
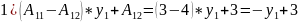
Стратегии игрока



Ответ: Так как стратегии игроков одинаковые ответ будет один и тот же
Х1 = 0,75 а Х2 = 0,25
