С одержание:

1. Введение;

2. Основная часть: Материал по теме, задание и его решение;

3. Заключение;

4. Список используемой литературы

Введение

Курсовая работа осуществляется на заключительном этапе изучения учебной дисциплины «Математические методы», кото­рая, в конечном счете, отражает степень усвоения студентом дисциплины профессиональной образовательной программы.

Настоящие методические указания разработаны в соответ­ствии с профессиональной образовательной программой по специальности 230105 «Программное обеспечение вычислительной техники и автоматизированных систем» и является итоговым контролем знаний студентов.

Целью настоящих методических указаний является оказа­ние помощи студентам в определении состава курсовой работы, ознакомлении с содержанием и оформлением курсовой работы, организацией ее защиты. Курсовая работа является са­мостоятельной работой будущего специалиста. Она дает кон­центрированную и достаточно полную характеристику знаний и умений студентов.

Целью выполнения курсовой работы является:

• систематизация, закрепление и расширение теоретических и практических знаний, полученных в процессе обучения;

• формирование умений применять теоретические знания при решении поставленных вопросов;

• формирование умений использовать справочную, нормативную и правовую документацию;

• развитие творческой инициативы, самостоятельности, от­ветственности и организованности,

В соответствии с поставленной целью при выполнении курсовой работы студент должен решить следующие задачи:

• проявить навыки и способности к правильному пониманию теоретических положений ранее изученных дисциплин;

• грамотно предлагать необходимые рекомендации, выполнять различные расчеты и логично излагать свои мысли;

Вариант – 6.

1. Задача линейного программирования

Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:

Ресурсы	Нормы затрат ресурсов на одно изделие		Общее количество ресурсов
	стол	шкаф
Древесина (м3): 1 вида	0,3	0,2	45
2 вида	0,2	0,4	65
Трудоемкость (человеко-ч)	1,4	1,6	395
Прибыль от реализации одного изделия (руб.)	7	9

Определить, сколько столов и шкафов фабрике необходимо изготавливать, чтобы прибыль от их реализации была максимальной.

Требуется:

1. Составить математическую модель задачи;

2. Решить задачу графическим методом.

1. Математическая модель

Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса:

1. Для определения каких величин строится модель?

2. В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?

3. Каким ограничениям должны удовлетворять неизвестные?

В нашем случае мебельной фабрике необходимо спланировать объем производства столов и шкафов так, чтобы максимизировать прибыль. Поэтому переменными являются:

X₁ – количество столов, X₂ – количество шкафов.

Суммарная прибыль от производства столов и шкафов равна Z = 7*Х₁ + 9*Х₂. Целью фабрики является определение среди всех допустимых значений X₁ и X₂ таких, которые максимизируют суммарную прибыль, т.е. целевую функцию Z.

Перейдем к ограничениям, которые налагаются на Х₁ и Х₂. Объем производства шкафов и столов не может быть отрицательным, следовательно:

Х₁,Х₂ ≥ 0

Нормы затрат древесины на столы и шкафы не может превосходить максимально возможный запас данного исходного продукта, следовательно:

0,3х₁ + 0,2х₂ ≤ 45

0,2х₁ + 0,4х₂ ≤ 65

Кроме того, ограничение на трудоемкость не превышает количества затрачиваемых ресурсов

1,4x₁ + 1,6x₂ ≤ 395

Таким образом, математическая модель данной задачи имеет следующий вид:

Максимизировал

Z = 7x₁ + 9x₂ > max

при следующих ограничениях:

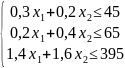
Заметим, что данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.