7

Московский государственный университет путей сообщения рф (миит) Кафедра «Физика-2»

Институт, група ИТТСУ, ВПЛ-111 К работе допущен __________________

(Дата, подпись преподавателя)

Студент Работа выполнена__________________

(Дата, подпись преподавателя)

Преподаватель Пыканов. И. В. Отчёт принят_______________________­­­ (Дата, подпись преподавателя)

Отчёт по лабораторной работе № 4 изучение свободных колебаний пружинного маятника

1. Цель работы:

Определение коэффициента жесткости пружины по удлинению пружины и методом колебаний пружинного маятника.

2. Приборы и принадлежности.

Штатив с пружиной и зеркальной шкалой, держатель для грузов, набор грузов, секундомер.

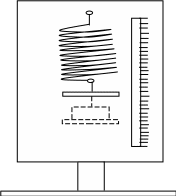
3. Основные теоретические положения к данной работе

Рассмотрим простейшую колебательную систему: груз массой m, подвешенный на пружине. Упругая сила растяжения пружины в положении равновесия равна силе тяжести груза и, будучи направлена вверх, уравновешивает ее. При выведении груза из положения равновесия пружина действует на него с дополнительной силой F, пропорциональной смещению x (при малых смещениях) и направленной в сторону противоположную смещению:

F  – kx,

где k – коэффициент жесткости пружины; он равен численному значению силы, которую нужно приложить к пружине, чтобы растянуть (или сжать) ее на единицу длины. Единица измерения коэффициента жесткости – [k]  Нм^1.

Груз, выведенный из положения равновесия, начнет совершать относительно него гармонические колебания:

x  A sin (ωt + φ₀), (1)

где А – амплитуда колебания; (ωt + ₀) – фаза колебания; ω - круговая частота; ₀ - начальная фаза колебания.

Энергия, сообщенная системе пружина-груз при начальном толчке, будет периодически преобразовываться: потенциальная энергия упруго деформированной пружины Е_n  будет переходить в кинетическую энергию движущегося груза Е_k  и обратно.

Согласно закону сохранения энергии для консервативной системы механическая энергия

E  Е_n + Е_k  +  const. (2)

В момент прохождения грузом положения равновесия (x  0) из формулы (2) следует, что полная энергия системы

E  Е_{k max}  .

Согласно уравнению (1), скорость гармонически колеблющегося груза

   Aωcos(ωt  ₀),

а максимальная скорость

_max  ωA. (3)

В крайних положениях груза (  0, x  ±A) энергия системы переходит полностью в потенциальную Е_п:

E  Е_{п max}  .

По закону сохранения энергии

 . (4)

Подставляя выражение (3) в соотношение (4), получим

mω²  k, ω  .

Учитывая, что ω  , получим выражение для периода колебаний Т:

T  2 . (5)

Таким образом, период не зависит от амплитуды колебаний и определяется только величинами m и k. Амплитуда и начальная фаза колебаний φ₀ определяются начальными условиями, при которых возникло движение.