1.5 Экспоненциальное распределение

В различных приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике и т.д. широко применяется экспоненциальное (показательное) распределение.

Время занятости канала связи, время безотказной работы ЭВМ, продолжительность поиска чего–либо – все это экспоненциально распределенные случайные величины.

Неотрицательная величина X называется распределенной по экспоненциальному закону, если ее плотность распределения имеет вид

,

где - параметр экспоненциального распределения.

График плотности распределения изображен на рис. 13.

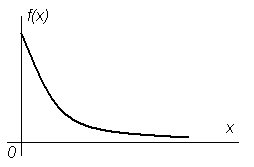
Рисунок 13 График плотности вероятности экспоненциально распределенной случайной величины

Определим основные числовые характеристики этого распределения:

,

т.е. математическое ожидание есть величина обратная параметру закона. Для отыскания дисперсии используем формулу

. Откуда средне – квадратичное отклонение будет равно

.

Вероятность попадания случайной величины на заданный участок, распределенной экспоненциально можно рассчитать, используя формулу

.

1.6 Обработка результатов измерений

Всякое измерение, каким бы способом и как бы тщательно оно ни проводилось, неизбежно сопровождается некоторой ошибкой. При проведении большого числа измерений какой – либо величины результаты измерений почти всегда будут отличаться друг от друга. Причины ошибок измерений могут быть самыми разнообразными.

Случайной ошибкой называют такую ошибку, которая при различных измерениях может изменять свой знак и величину, причем заранее нельзя указать, какое значение и какой знак примет ошибка в данном опыте.

При изучении тех или иных явлений возникает задача определения вида закона распределения случайных ошибок, сопровождающих измерения, и их параметров.

1.6.1 Выборка, ряды распределения

При изучении качественного и количественного признака, характеризующего множество некоторых однородных элементов, не всегда имеется возможность исследовать каждый из них. Поэтому в целях получения информации об этом множестве исследуют только некоторую небольшую часть ее элементов, отобранных совершенно случайно. Практика подтверждает, что выводы, сделанные в результате анализа этой части элементов, бывают достаточно объективными и для всего изучаемого множества.

Множество всех элементов, подлежащих изучению, называют генеральной совокупностью. В отличие от нее выборка – конечная совокупность элементов, отбираемых из генеральной совокупности, для статистического вывода о свойствах генеральной совокупности на основании свойств отобранных элементов.

Любое статистическое исследование всегда связано с производством выборки. Выборка должна быть представительной, т.е. такой, чтобы любой элемент генеральной совокупности мог попасть в нее с вероятностью, не зависящей от характеристик подлежащих измерению.

Число элементов генеральной совокупности (выборки) называют ее объемом.

Пример 1. Из партии, содержащей 10000 деталей, отобрали случайным образом для проверки 80 деталей.

Объем генеральной совокупности в данном примере равен 10000, а объем выборки – 80.

Очевидно, что чем больше объем выборки, тем более полное представление можно получить о генеральной совокупности.

Исследование выборки сводится к отысканию ее статистик (функций выборки), к которым относят: вариационный ряд, статистическое распределение выборки, эмпирическую функцию распределения, гистограмму, среднее арифметическое результатов наблюдений и т. п. Статистики, используемые для приближенной оценки параметров генеральной совокупности, называют также статистическими оценками.

Статистическое распределение выборки отражает соответствие между наблюдаемыми значениями и их частотами или относительными частотами.

Пусть из генеральной совокупности извлечена выборка объема n, причем наблюдалось раз, раз, …, , где .

Наблюдаемые значения называют вариантами, последовательность же вариантов, расположенных в возрастающем порядке, - вариационным рядом.

Число , показывающее, сколько раз встречается вариант в выборке, называют частотой варианта.

Отношение частоты варианта к объему выборки n называют относительной частотой: .

С учетом этих определений под статистическим распределением выборки понимают перечень вариант и соответствующих им частот или относительных частот .

Пример 2 Задано статистическое распределение частот (Таблица 5.1):

Таблица 5.1

	2	5	7
	1	3	6

Объем выборки n=10. Находим относительные частоты:

и составляем статистическое распределение относительных частот (таблица 5.2):

Таблица 5.2

	2	5	7
	0.1	0.3	0.6

В целях наглядности соответствия между наблюдаемыми вариантами и частотами или относительными частотами распределение выборки изображают графически.

Для этого точки последовательно соединяют отрезками прямой. Получающаяся при этом ломаная линия называется полигоном частот; если же последовательно соединить отрезками прямой точки , то – полигоном относительных частот.

Эмпирическую функцию распределения также как статистическое распределение выборки и полигон применяют для изображения дискретного вариационного ряда. Эмпирической функцией распределения называют отношение числа вариант, значения которых меньше некоторого фиксированного значения варианта, к объему выборки, т.е.

,

где - число вариант, значения которых меньше некоторого фиксированного значения варианта.

Пусть произведено n независимых опытов и по данным выборки сформирован вариационный ряд . Для построения графика эмпирической функции распределения определяют ее значения в точках следующим образом. .

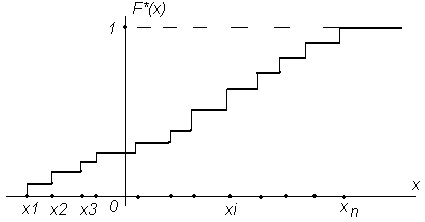
Рис.5.1 – График эмпирической функции распределения

График эмпирической функции распределения (рис.5.1) является случайным. Для уменьшения случайности функции график сглаживают. По этому графику приближенно определяют вид истинной функции распределения случайной величины.

Гистограмма частот или относительных частот. Если выборочные данные относятся к непрерывной случайной величине, то интервал, в котором заключены все наблюдаемые значения, разбивают на частичные интервалы длиной h и находят для каждого частичного интервала сумму частот вариант , попавших в i – й интервал.

Затем строят ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные интервалы длиной и высотой, равной отношению или .

Отношение называют плотностью частоты, а отношение называют плотностью относительной частоты, поэтому и, построенная таким образом, ступенчатая фигура носит название гистограммы частот или гистограммы относительных частот.

Для построения гистограммы частот или относительных частот (рис.5.2) по статистическому распределению выборки необходимо составить таблицу 5.3, в которой отобразить номера и положение частичных интервалов, суммы частот вариант, плотности частот и относительных частот в этих частичных интервалах.

Таблица 5.3

Номер частичного интервала	Частичный интервал	Сумма частот вариант	Плотность частот	Плотность относительных частот
1	1 – 5	10	2.5	0.025
2	5 – 9	20	5	0.05
3	9 – 13	50	12.5	0.125
4	13 – 17	12	3	0.03
5	17 – 21	8	2	0.02

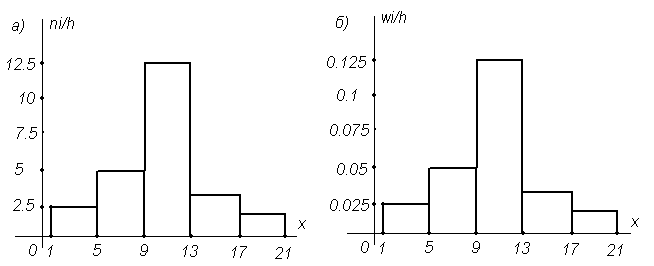
Рисунок 5.2 – Гистограмма частот (а) и относительных частот (б)

Обе гистограммы (рис.5.2) по форме одинаковы и отличаются лишь масштабом по оси ординат. Площадь гистограммы относительных частот, как и площадь плотности распределения случайной величины, равна единице, что позволяет определять вероятность попадания случайной величины в заданный интервал путем вычисления площади части гистограммы, ограниченной этим интервалом.