1.3 Закон равномерной плотности

К наиболее распространенным в природе законам распределения относят следующие: закон равномерной плотности, нормальный закон распределения, закон Пуассона и экспоненциальное распределение. Рассмотрим их более подробно.

Случайную непрерывную величину X называют распределенной равномерно на интервале (a, b), если ее плотность распределения на этом интервале постоянна, а вне этого интервала равна нулю.

Пусть случайная величина X может принимать частные значения от a до b, причем все частные значения равновероятны (Рис.7). Требуется определить выражение для плотности вероятности f(x).

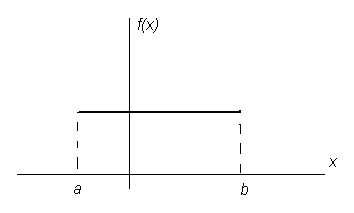
Рисунок 7 График плотности распределения случайной величины X

Для определения выражение для плотности вероятности f(x) воспользуемся свойством плотности распределения

.

Поскольку по определению f(x) есть величина постоянная, то ее можно вынести за знак интеграла, т.е.

. Откуда .

Зная выражение для плотности вероятности f(x), можно найти функцию распределения как

.

График функции равномерного распределения в соответствии с этим выражением примет вид, изображенный на рис.8.

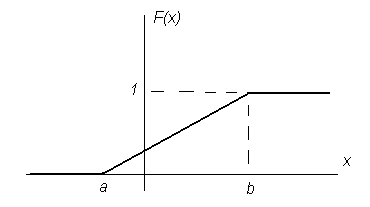
Рисунок 8 График функции равномерного распределения

При известном выражении для плотности равномерного распределения нетрудно вывести выражения, позволяющие вычислить математическое ожидание, дисперсию и средне - квадратичное отклонение для этого закона

; ; .

Вероятность попадания случайной величины на заданный участок.

Пусть случайная величина X распределена равномерно на интервале от a до b, причем плотность вероятности ее известна и равна f(x)=1/(b-a). Требуется определить вероятность попадания ее на участок от c до d (рис.9), т.е. .

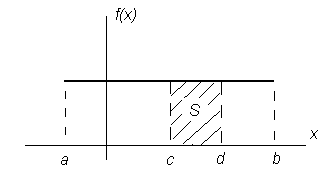
Рисунок 9 Определение вероятности попадания случайной величины на заданный участок

Определяя эту вероятность как интеграл от плотности вероятности f(x), получаем

.

Следовательно, вероятность попадания случайной величины на заданный участок от c до d определяется как площадь заштрихованного прямоугольника.

Округление результатов измерений имеет равномерное распределение.

1.4 Нормальный закон распределения

Одним из наиболее часто встречающихся законов распределения случайной величины является нормальный закон (закон Гаусса). Он является доминирующим над другими законами распределения и играет особую роль в различных приложениях теории вероятностей.

Такие случайные величины, как ошибки измерений, отклонение точки попадания от центра цели, отклонение размеров детали от заданного номинала при массовом производстве, мгновенные значения шумового напряжения подчиняются нормальному закону.

Нормальным называют распределение случайной непрерывной величины, плотность распределения которой имеет вид

,

где a и - параметры нормального распределения.

Нормальное распределение возникает в тех случаях, когда на появление значений случайной величины влияет много различных факторов.

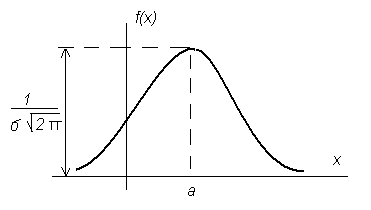
Рисунок 10 График плотности нормального распределения

Из кривой нормального распределения (рис.10) следует, что значения случайной величины, которые располагаются ближе к величине a, будут появляться чаще.

Выясним вероятностный смысл параметров нормального распределения. Для этой цели определим основные числовые характеристики

.

Введем новую переменную и выразим подынтегральное выражение через нее:

.

Пределы интегрирования не изменяются, следовательно,

.

Первый интеграл, стоящий в правой части полученного равенства, равен нулю, так как подынтегральная функция нечетна, и пределы интегрирования симметричны, второй же есть интеграл Пуассона, равный , и окончательно получим, что

.

параметру a.

Поступая аналогично, получим, что .

Из полученных результатов следует, что параметр нормального распределения a представляет собой математическое ожидание (центр рассеивания), а параметр является характеристикой рассеивания.

Оценим влияние параметров нормального распределения на форму кривой. Так как разность x-a в аналитическом выражении функции содержится во второй степени, то кривая распределения будет симметрична относительно прямой x=a.

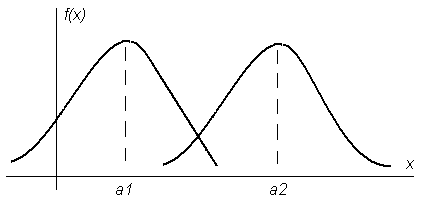
Рисунок 11 Влияние параметра a на форму кривой

Изменение параметра a не влияет на форму кривой, а приводит лишь к сдвигу ее вдоль оси абсциссы вправо, если он возрастает (a2>a1), и влево, если убывает (рис. 11).

Изменение параметра влияет на форму кривой: если он возрастает, то максимальная ордината убывает и кривая распределения становится более пологой, если же убывает, то максимальная ордината возрастает и кривая становится более острой (рис. 12).

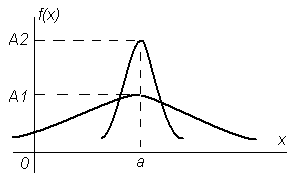
Рисунок 12 Влияние параметра на форму кривой

Ординаты точек A1 и A2 соответственно равны:

где .

При любых значениях параметров a и площадь, ограниченная кривой Гаусса и осью абсцисс, остается равной единице.

Вероятность попадания нормально распределенной случайной величины на заданный участок можно найти по формуле

.

Введем новую переменную , тогда ; пределы интегрирования соответственно будут:

.

Следовательно,

.

Окончательно искомая вероятность будет равна

,

где .

Функция Лапласа Ф(x) или интеграл вероятности является табличным, что позволяет, пользуясь таблицей, найти вероятность попадания нормально распределенной случайной величины на заданный участок , если известны параметры a и .

Правило трех сигм. Для определения правила установим вероятность отклонения нормально распределенной случайной величины от своего математического ожидания в зависимости от выбранного значения . С этой целью придадим значения :

;

;

.

Из полученного результата следует, что вероятность отклонения нормально распределенной случайной величины от своего математического ожидания больше чем на три сигма незначительна, меньше 0,3%.

Следовательно, большинство значений нормально распределенной случайной величины сосредоточены около центра рассеивания (математического ожидания) в полосе трех сигм.

На практике правило трех сигм позволяет распределение изучаемой величины относить к нормальному распределению, если максимальное отклонение значений ее не превышает трех сигм.