
- •3 Системы случайных величин
- •3.1 Понятие системы случайных величин
- •3.2 Функция распределения системы двух случайных величин
- •3.3 Плотность распределения системы двух случайных величин
- •3.4 Законы распределения отдельных случайных величин, входящих в систему
- •3.5 Закон распределения системы случайных дискретных величин
- •3.6 Условные законы распределения случайных величин
- •3.7 Зависимые и независимые случайные величины
- •3.8 Числовые характеристики системы двух случайных величин
3.5 Закон распределения системы случайных дискретных величин
Пусть имеется система случайных величин (X, Y) , закон распределения которой задан таблицей 3.1.
Таблица 3.1
-
Xi Y j
Y1
Y2
…
Y j
…
Y m
X1
p(x1,y1)
p(x1,y2)
p(x1,yj)
p(x1,ym)
X2
p(x2,y1)
p(x2,y2)
p(x2,yj)
p(x2,ym)
...
X i
p(xi,y1)
p(xi,y2)
p(xi,yj)
p(xi,yj)
…
X n
p(xn,y1)
p(xn,y2)
p(xn,yj)
p(xn,ym)
В ячейках таблицы расположены вероятности того, что случайные величины X и Y примут i – тое и j – тое частные значения, т.е.
![]() .
.
Для получения закона распределения случайной величины, входящей в систему пользуются формулами:
![]() ,
,
![]() .
.
Пример 2. Дана система случайных величин (X, Y), закон распределения которой задан таблицей 3.2.
Таблица 3.2
|
X1=1 |
X2=2 |
X3=3 |
Y1=2 |
0,1 |
0,2 |
0,1 |
Y2=4 |
0,2 |
0,3 |
0,1 |
Требуется определить законы распределения случайных величин X и Y.
Решение.
Определяем вероятности того, что случайная величина X случайная величина примет значения 1;2;3, а случайная величина Y - значения 2;4:
![]() .
.
Производим проверку суммированием вероятностей, которая должна быть равна единице по каждой случайной величине, т.е.
![]() .
.
Следовательно, законы распределения случайных величин X и Y определены правильно.
3.6 Условные законы распределения случайных величин
Ранее были получены формулы для нахождения плотностей распределения составляющих величин по плотности распределения системы двух случайных величин f(x, y).
В ряде случаев бывает необходимо определять плотность распределения системы двух случайных величин f(x, y) по известным плотностям распределения отдельных случайных величин , входящих в систему.
Для решения этой задачи кроме плотностей распределения отдельных случайных величин необходимо знать их взаимные связи и зависимость между ними. Эта зависимость характеризуется условными законами распределения, которые являются аналогами условных вероятностей.
Условным законом распределения случайной величины X, входящей в систему (X, Y) называют ее закон распределения, вычисленный при условии, что другая случайная величина Y приняла определенное значение y.
Условные функции распределения случайных величин X и Y будем обозначать через F(x/y) и F(y/x) соответственно, а условные плотности распределения – через f(x/y) и F(y/x).
Постановка задачи. Пусть имеется система случайных величин (X, Y), причем известна ее плотность распределения f(x, y). Требуется найти условную плотность распределения f(x/y) случайной величины X при условии, что случайная величина Y приняла определенное значение y.
Для решения задачи рассмотрим элементарный прямоугольник со сторонами d x, d y (рис. 3.8).

Рисунок 3.8 Элементарный прямоугольник со сторонами d x, d y
Обозначим через C – событие попадания случайной точки в прямоугольник C, через A - событие попадания случайной точки в полосу A, а через B - событие попадания случайной точки в полосу B.
Так как событие C является произведением событий A и B, поскольку может произойти только при появлении и события A и события B, то вероятность события C можно определить с помощью теоремы произведения зависимых событий, т.е.
![]() .
.
Откуда
![]() ,
но
,
но
![]() и
и
![]() .
.
Тогда
![]() .
Разделив обе части этого равенства на
.
Разделив обе части этого равенства на
![]() ,
получим
,
получим
![]() .
В этом выражении отношение
.
В этом выражении отношение
![]() ,
так как оно представляет собой количество
условной вероятности, приходящейся на
единицу длины случайной величины X,
т.е. является условной плотностью
распределения случайной величины X,
при условии, что случайная величина Y
приняла
определенное значение
y.
,
так как оно представляет собой количество
условной вероятности, приходящейся на
единицу длины случайной величины X,
т.е. является условной плотностью
распределения случайной величины X,
при условии, что случайная величина Y
приняла
определенное значение
y.
Следовательно,
 ,
а
,
а
 .
.
Пример 3. В условиях примера 1 определить условную плотность распределения f(x/y) случайной величины X.
Решение. Так как
,
![]() ,
,
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() .
.
Если случайные величины дискретные, то вместо условных плотностей распределения определяются условные вероятности
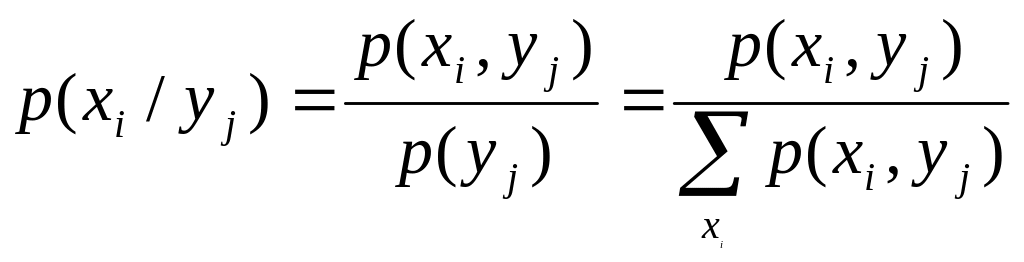 ,
а
,
а
 .
.
