2. Непараметрические методы классификации.

В настоящем параграфе рассматриваются методы оценки плотностей и методы классификации наблюдений, не предполагающие известных (с точностью до параметров) плотностей наблюдений, принадлежащих к разным классам. Однако мы будем предполагать наличие обучающих выборок из каждого класса. В параметрических задачах классификации эти выборки служили для оценки неизвестных параметровплотностей, т. е. для оценок самих этих плотностей. В непараметрических задачах они необходимы также для оценки плотностей, только теперь это будут так называемые непараметрические оценки плотностей, в некотором смысле - многомерный аналог гистограммы.

Методы классификации, опирающиеся на эти оценки, как и в работе [7] будем называть локальными, так как отнесение наблюдения Z к тому или иному классу будет зависеть от ближайших к нему точек обучающих последовательностей. Поэтому требуются дополнительные предположения относительно понятия близости наблюдаемых точек.

а) Методы, использующие понятие близости. Понятие близости можно задавать, например, следующим образом. Определим в пространстве наблюдаемых признаков некоторую окрестностьточки 0 =(0,0,..,0).

Задаваясь произвольным действительным числом r > 0 и сопоставляя каждой точке U из окрестности нуля точку, мы получим отображение окрестностив некоторую подобную ей окрестность. Меняяr, будем иметь систему подобных окрестностей около точки 0. Тогда для произвольной точкиZ при заданном виде окрестности нуля можно рассмотреть соответствующие подобные окрестности (см. рис. 1.6).

.

Таким образом, очевидно, что при заданных иZ для любой p-мерной точки факторного пространства можно определить множество действительных чисел таких, что если только , то.

Соответственно полагают, что из двух точек Х и Y точка Х расположена ближе к точке Z (в смысле окрестности , чем точкаY, если .

Обычно понятие близости точек наиболее естественно вводится через расстояние в пространстве признаков. В этом случае областипревращаются в систему «сфер» радиусаr и центром в точке Z.

Приведем вначале несколько способов классификации объекта Z, а затем остановимся более подробно на различных локальных оценках плотностей и отношений правдоподобия в точке Z, на основании которых производится классификация.

Методы классификации точки Z могут состоять в следующем.

1) В зависимости от объемов обучающих выборок определяется число k:

- рассматривается k ближайших к Z точек из обучающих выборок;

- точка z относится к тому классу i, из которого в числе k ближайших точек присутствует больше точек, чем точек из любого другого класса .

При двух классах и нечетном k этот метод наиболее хорошо изучен [12] и обязательно относит точку Z к одному из классов.

2) В зависимости от объемов m_i обучающих выборок класса i выбираются числа k_i:

- около точки Z для каждого i строится окрестность наименьшего радиуса_i такая, что она содержит не менее k_i точек из обучающей выборки класса i. Заметим, что определенный таким образом радиус _i является величиной случайной;

- точка Z относится к тому классу i, для которого .

3) По непараметрическим оценкам плотностей около точки Z и, следовательно, по оценке функций (или разделяющих поверхностей), точкаZ относится к одному из классов аналогично тому, как это делалось в § 2 настоящей главы.

Приведем некоторые общие результаты, которые показывают состоятельность наиболее изученного метода классификации (метод 1) на два класса при и. Черезобозначим плотность распределения точек, принадлежащих к одному классу, а через- число точек обучающей последовательности, попавших в область.

Теорема 2 [11]. Если - непрерывная функция в точкеZ и при,, то величина

является состоятельной оценкой плотности в точкеZ.

Для евклидова расстояния и сферы аналогичные результаты получены в работе [14].

Если и точки обучающих последовательностейиупорядочены в порядке возрастания расстояний,от точкиZ и взята k-я по расстоянию от Z точка , то черезбудем обозначать число точек из последовательностис меньшими (не большими) чемрасстояниями доZ, а через - число таких же точек из последовательности. В этом случае справедлива следующая теорема.

Теорема 3 [7]. Если плотности иразных классов непрерывны в точкеZ и число выбрано так, что,,,при,(но при этом), то величина является состоятельной оценкой для отношения плотностей.

В случае, когда семейство плотностей параметрическое иииспользуется непараметрический критерий для классификации точкиZ, известна [11].

Теорема 4. Если для всех  и для почти всех U (по мере ) оценкасостоятельна для, то правило классификации

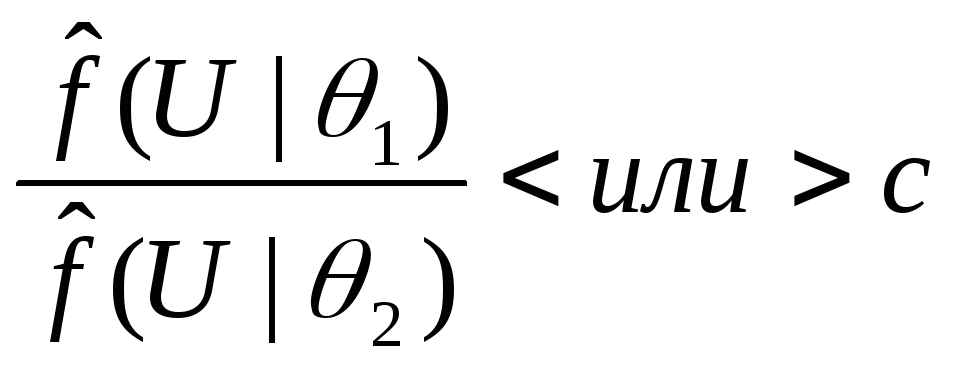
состоятельно над семейством . С помощью теоремы 2 в работе [7] строится состоятельная оценка для (метод 2)

где p - размерность каждого наблюдения, а k_i - фиксированное число точек в области .

В этом случае - асимптотически несмещенная (при) оценкаи ее можно использовать для оценки отношения плотностей.

Если области различны для распределенийи для, атакие, что в областьпопадает равноk₁ и k₂ точек последовательностей и, объемови, то

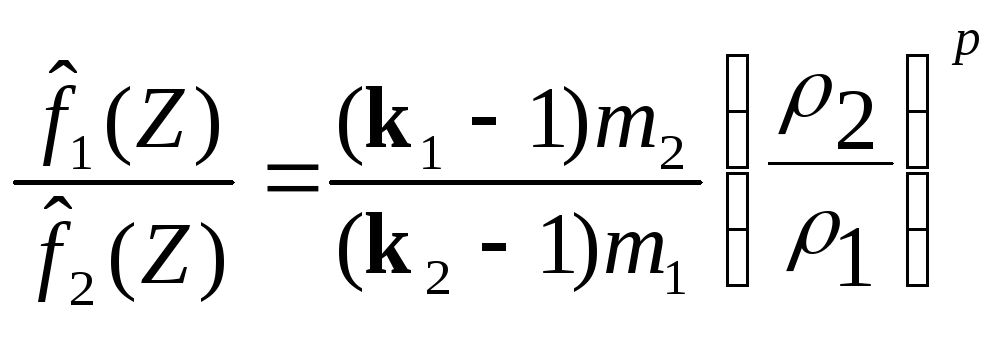
является состоятельной оценкой отношения правдоподобия в точке Z.

При иk₁ = k₂ это правило совпадает с известным [11] при (метод 1).

В работе [7] предлагается выбирать величину

для . Отличаясь от параметрических методов меньшими требованиями на плотности, локальный метод имеет ряд существенных недостатков. Отметим лишь некоторые из них:

при оценке отношения правдоподобия используются лишь точки, входящие в уменьшающуюся с ростомокрестность классифицируемой точкиZ. Это приводит к тому, что порядок сближения (при ) этого метода с наилучшим (основанном на) хуже, чем для параметрических процедур, которые используют все данные обучения при классификации точкиZ;

локальный метод классификации требует большей вычислительной работы при классификации новых данных, чем при параметрическом методе классификации и наличии обучения. Например, при классификации нормальных наблюдений с помощью линейной разделяющей поверхности достаточно знать лишь р+ 1 чисел, а при локальном методе классификации требуется помнить всечисел.

Локальный метод, устраняя одну трудность - наличие сведений об общем виде распределения наблюдений, - сразу же заменяет ее другой - трудностью выбора расстояния между точками-наблюдателями. Эту трудность можно преодолеть, как будет показано ниже, заменив ее другой неопределенностью.

Остановимся коротко на некоторой модификации правила классификации (1), описанного выше. Эта модификация для двух классов описана, например, в работе [13] и состоит в том, что можно для точки Z принимать, как описано в § 2, п. 4, три решения:

- отнести точку к классу i () и- воздержаться от принятия решения.

Предлагается следующая процедура:

в зависимости от и- числа точек обучающих последовательностей выбираются числаk и ;

выбираются k ближайших к точке Z точек из множества точек обучающих выборок;

точка Z относится к классу i (), если в числеk ближайших точек имеется более k' точек из обучающей выборки класса i. Если же этого не происходит, то принимается решение . Это означает, что в числе ближайших кZ точек примерно поровну точек классов 1 и 2.

В работе [13] показано, что при априорных вероятностях классов _i, и,, предлагаемая процедура сходится к байесовской, описанной в § 2, п. 4, т. е. являетсясостоятельной.

Очевидно, что при k нечетном и эта процедура совпадает с описанной в работах [11] и [12].

б) Методы, использующие понятия весовой функции. В пространстве выборочных точек можно отказаться от введения расстояния, не изменяя при этом качества алгоритмов классификации (состоятельность и т. д.). Но в этом случае приходится вводить произвольную функцию веса , которая должна удовлетворять следующим условиям [26].

Функция K должна быть неотрицательна, симметрична, монотонно-мажорируема и интегрируема, т. е.

;

;

,где

при ;

.

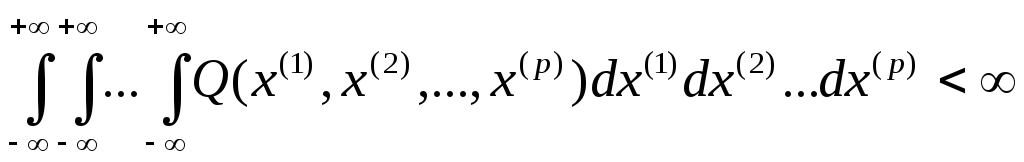Вполне естественно, что в качестве весовой функции можно взять любую интегрируемую в области от 0 до и неотрицательную функцию одномерного параметра, где вместо аргументаz стоит норма . Еслиеще и монотонно убывающая функция, то последние условия автоматически выполняются. Условиебез ограничения общности можно заменить условиеми взять вместо функции весамажоранту, если мажоранта симметрична. Если выбрать ещеp последовательностей , таких, чтопри, апри, то можно получить оценку плотности в точке

,

где () - точки обучающей выборки из какого-либо класса.

В этом случае при вышеприведенных условиях можно доказать [16], что оценка состоятельна в точках непрерывностиZ плотности , а величина

асимптотически () нормальна с математическим ожиданием 0 и единичной дисперсией.

Легко проверить, что последовательности удовлетворяют всем необходимым условиям. Для таких последовательностей сходимость оценкиf^ (Z) к плотности определяется скоростью убывания дисперсии, равной

.

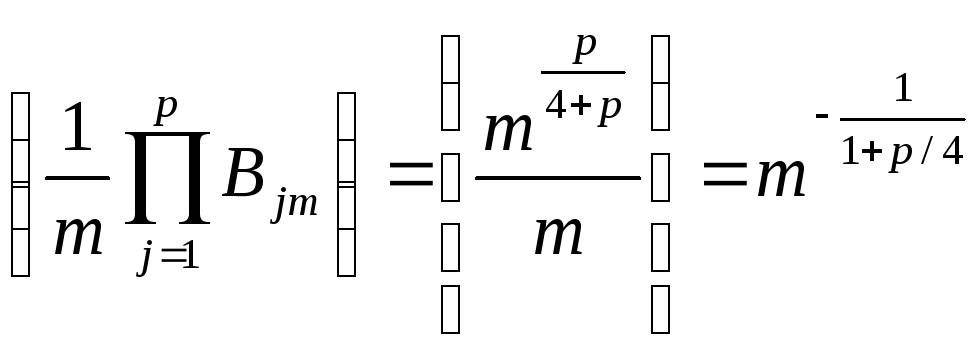Следовательно, скорости сближения оценок в методах, описанных в работе [7] и в работе [16], совпадают для этого частного случая и равны . Очевидно, что функции

и т. д.,

на которых основаны методы классификации с помощью так называемых потенциальных функций (см. главу III), удовлетворяют всем необходимым условиям построения локальных оценок плотностей.

В работе [5] доказано, что оценка плотности с весовой функцией обладает всеми приведенными выше свойствами, хотя функцияможет принимать и отрицательные значения. Поэтому от условия неотрицательности можно отказаться.

в) Эвристический метод классификации¹.

Пусть имеется обучающая выборка () объема, и эта выборка разбита наk классов . Предъявляется элемент, подлежащий классификации, и производится подсчет числа голосов за l-й класс следующим образом. Выбирается , гдер - размерность пространства Х и рассматриваются любые р' координат p-мерного вектора X. Пусть этот набор координат обозначен через П, а через для любогообозначается величина

.

Введем функцию

.

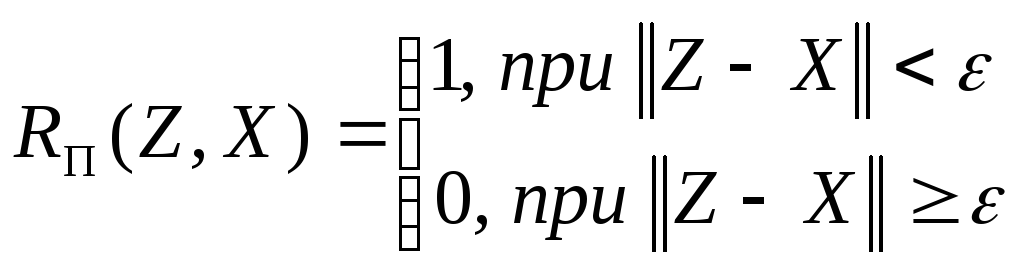Возьмем любой вектор . Определим величину

.

Суммирование здесь ведется по всевозможным наборам р' координат из р (число таких наборов- равно ). Тогда величинаравна

.

Пусть задано некоторое число . Векторотносится к тому классуl, при котором

для всех . Если такогоl не существует, то вектор Z не может быть классифицирован.

В целях проверки качества классификации описанный выше алгоритм применяется для классификации элементов обучающей выборки. Затем подсчитывается некоторая величина Е, характеризующая качество алгоритма, которая выражается через число неправильно классифицированных объектов и через число объектов не классифицированных в процессе работы алгоритма. Очевидно, что значение Е зависит от (k, , ). Выбираются те значения k, ,  при которых Е достигает экстремума.