Глава II

КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ.

ПАРАМЕТРИЧЕСКИЙ СЛУЧАЙ: РАСЩЕПЛЕНИЕ СМЕСЕЙ

НА ОСНОВЕ ОЦЕНКИ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ

§ 1. Смеси и условия их различимости

Прежде чем приходить к формальному описанию смеси, остановимся на простейшем примере. Допустим, что необходимо распознавать рукописные цифры, соответствующие 0, 1, 2, ..., 9. Каждая цифра, например 8, может быть написана многими способами, соответствующими почеркам различных людей. Таким образом, мы будем иметь дело с целой группой написаний, которые относятся к понятию цифры 8, т. е. будем иметь дело с однородной группой написаний.

Но различных цифр десять, поэтому можно говорить о смеси десяти однородных групп, соответствующих различным цифрам. Следовательно, при разбиении совокупности рукописных цифр на группы мы сталкиваемся со смесью не более чем десяти однородных в некотором смысле групп.

При разбиении совокупности городов (семей, производственных предприятий, стран) на однородные группы, естественно, могут наблюдаться аналогичные явления. Поэтому каждая однородная группа обладает какими-то общими признаками и каждый объект этой группы может иметь индивидуальные (случайные) отличия.

Говоря более формально, каждая однородная группа может быть представлена в виде генеральной совокупности, задаваемой своей функцией плотности распределения вероятностей f(U|), где параметр  может играть, например, роль номера класса.

Часто при классификации объектов, как в нашем примере, имеют дело не с одной, а с целой серией (конечной или бесконечной) однородных групп, каждая из которых представлена в некоторой пропорции, т. е. имеют дело со смесями однородных групп. При этом возникает задача: выяснить, имеем ли мы дело со смесью или с одной однородной группой, другими словами, не является ли смесь однородных в некотором смысле групп, однородной группой в том же самом смысле.

1. Математическая постановка задачи

Пусть имеется семейство плотностей распределений

и пусть G = {G()} - семейство смешивающих распределений. Мы не включаем в G неинтересный для нас случай так называемых вырожденных распределений I, т. е. таких функций G(), которые, имеют скачок от 0 до 1 в одной точке. Функция плотности распределения, или (интеграл в смысле Лебега- Стильтьеса) называется смесью (G-смесью) семейства F. Когда G() пробегает все точки класса пробегает классH, называемый классом смесей.

Класс смесей Н различим, или проще, смесь h(U) различима, если из равенства

следует, что для всех.

Если все смешивающие функции имеют скачки в конечном числе дискретных точек, а в остальных точках не изменяются, то класс смесей называется классом конечных смесей.

Возможность различимости класса конечных смесей

означает, что из соотношения

следует ; для любого найдется такое, что и. Примеры различимых и неразличимых смесей появятся несколько позже.

2. Некоторые свойства классов различимых смесей

Семейство F аддитивно замкнуто, если для любых ₁ и ₂

.

Символ * означает обычную операцию свертки, т. е.

.

Если  - одномерный параметр, т. е. m = 1, то класс смесей Н аддитивно-замкнутого семейства различим [10, 11].

Для конечных смесей известно еще несколько свойств [7]. Для различимости класса конечных смесей конечного семейства необходимо и достаточно, чтобы существовало k действительных чисел для которых матрица была. бы невырождена. Отсюда, в частности, следует, что классы конечных смесей конечного семейства нормальных и Г-распределений различимы.

Для различимости класса Н конечных смесей, но бесконечного семейства F необходимо и достаточно, чтобы семейство было линейно, независимо по параметрам [7].

Отсюда следует, что:

- семейство F₁ конечных произведений (р - целое положительное число множителей) экспоненциальных распределений различимо, т. е. образует класс различимых смесей;

- семейство p-мерных нормальных распределений F₂ образует различимые конечные смеси;

- семейство образует различимые конечные смеси;

- множество конечных смесей распределений Коши различимо;

- - плотность распределения с одномерным параметром. Семейство F плотностей с параметром сдвига образует различимые конечные смеси.

Таким образом, очень широкий класс конечных смесей различим. Чтобы не создалось ложного впечатления, что неразличимых смесей нет, приведем несколько примеров.

Пример 1. Рассмотрим семейство одномерных нормальных распределений, задаваемых плотностями , где, т. е. неизвестно ни математическое ожиданиеу, ни дисперсия ². Рассмотрим класс нормальных смешивающих распределений , гдеa и ² - какие-либо неизвестные числа. В этом случае смесь

принадлежит семейству нормальных распределений и поэтому может быть представлена следующим образом

.

Наконец, , гдеи имеет скачок в точкеа. Это значит, что нормальная смесь может быть представлена несколькими разными способами, т. е. является либо одним представителем класса, либо бесконечной смесью различных представителей этого же класса Другими словами, специальная смесь различных наборов из представителей нормального класса, о котором мы ничего не знаем (т. е. ни средних, ни дисперсий) опять является набором представителей из того же нормального класса. А это означает, что о нормальной совокупности можно говорить как об однородной группе, так и о некоторой специальной смеси бесконечного числа однородных нормальных групп.

Пример 2. Пусть семейство состоит из равномерных распреде­лений с неизвестными параметрами, т. е. и плотность

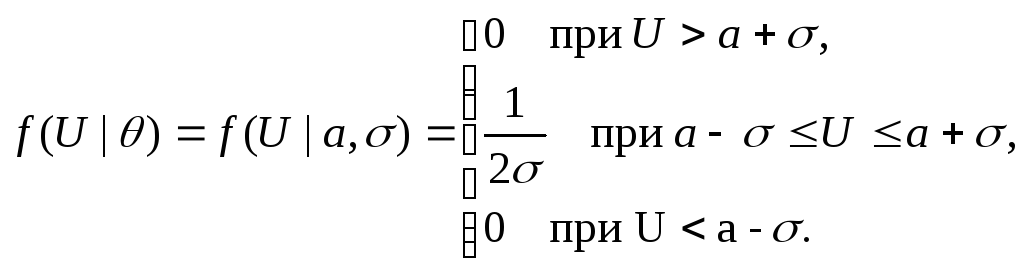
Рассмотрим класс конечных G-смесей, когда функция имеет лишь два скачка, что соответствует смешиванию двух различных однородных классов. Легко проверить (рис. 2.1), что для любого

.

Это означает, что смешивающая функция делает два скачка величины и (1 - ) и если , то. Аналогично можно произвести разбиение для любого числа классов. Другими словами, однородная группа представителей, которые могут появиться равновероятно в любой точке неопределенной области, может трактоваться как смесь (даже конечная) однородных групп представителей, однородных в том же смысле. Но если об области, где могут появляться представители, кое-что известно, например, в нашем случае = 1/2, то равномерное распределение уже нельзя разбить на смесь двух равномерных распределений с  = 1/2.

Пример 3. Рассмотрим семейство двумерных равномерных распределений на секторах круга единичного радиуса с центром в точке (0, 0). Сектор задается начальным направлением ср и углом при вершине  > 0, т. е. . Таким образом, для любых, ₁, ₂ .

,

что означает, что семейство смесей F неразличимо. Следовательно, равномерное распределение на круге с плотностью можно представить в виде

.

Это означает, что возможно любое разделение точек на два класса прямой, проходящей через центр (см. рис, 2.2).