5.5.2. Доказательство сходимости для случая коррекции по одной выборке

Исследование сходимости алгоритма спуска удобно начать с варианта, более легкого для анализа. Вместо определения по всем выборкам и осуществления коррекции по множеству классифи­цируемых с ошибкой выборок Y_k выборки будут рассматриваться последовательно, и весовой вектор будет изменяться всякий раз, когда некоторая выборка будет классифицироваться с ошибкой. Для доказательства сходимости подробная характеристика данной последовательности неважна, коль скоро каждая выборка появля­ется в последовательности бесконечно большое число раз. Наиболее просто убедиться в этом, повторяя выборки циклически.

Два последующих упрощения помогут лучшему пониманию из­лагаемого материала. Во-первых, временно ограничимся случаем, когда является константой. Это так называемый случай с постоян­ным приращением. Из соотношения (13) следует, что если — ве­личина постоянная, то она служит лишь для масштабирования выборок. Таким образом, в случае с постоянным приращением можно, без ущерба для общности, положить =1. Второе упроще­ние состоит лишь в введении обозначений. Когда выборки рассмат­риваются последовательно, некоторые из них классифицируются с ошибкой. Поскольку весовой вектор изменяют лишь при наличии ошибки, внимание фактически сосредоточивается только на выбор­ках, классифицируемых с ошибкой. Таким образом, последователь­ность выборок обозначается через y¹, у², . . . , у^k, . . . , где каждый у^k является одной из n выборок y₁, . . ., y_n и каждая выборка y^k классифицируется с ошибкой. Например, при циклическом повто­рении выборок y₁, у₂ и у₃, если отмеченные выборки

,,,,,,,,…

классифицируются с ошибкой, то последовательность y¹, у², у³, у⁴, у⁵, . . . обозначает последовательность y₁, у₃, y₁, у₂, у₂,. . . . Исходя из данного объяснения, для образования последовательно­сти весовых векторов может быть записано правило постоянного приращения:

(14)

где для всехk.

Правило постоянного приращения является простейшим из чис­ла многих алгоритмов, которые предлагались для решения систем линейных неравенств. Впервые оно появилось при введении схемы обучения с подкреплением, предложенной Ф. Розенблаттом для его персептронной модели мозга и доказательства сходимости послед­ней, известного под названием теоремы сходимости персептрона.

В частности, можно дать ее геометрическую интерпретацию в весо­вом пространстве. Поскольку вектор классифицирует у^k с ошиб­кой, то не будет находиться с положительной стороны у^k, при­надлежащего гиперплоскости . Прибавление у^k к вектору смещает весовой вектор непосредственно в направлении к данной гиперплоскости при возможности ее пересечения (рис. 5.10). Неза­висимо от того, пересечется ли гиперплоскость или нет, новое ска­лярное произведение будет больше прежнего

Рис. 5.10.Шаг, соответствующий правилу постоянного приращения.

произведения на величину ||у^k||², в результате получаем, что вследствие кор­рекции весовой вектор смещается в нужном направлении.

Покажем теперь, что, если выборки линейно разделяемы, после­довательность весовых векторов будет ограничиваться вектором решения. При доказательстве необходимо отметить, что каждая процедура коррекции сдвигает весовой вектор ближе к области решения. То есть следует показать, что если является любым вектором решения, то значение ||a_k+1—|| меньше значения ||а_k— ||. Хотя в общем случае данное утверждение оказывается неспра­ведливым, будет показано, что оно выполняется для векторов реше­ния, имеющих достаточную длину.

Пусть — вектор решения, так что величина у_i строго положи­тельна для всех i, a — положительный скалярный коэффициент. Из соотношения (14) следует, что

тогда

Поскольку у^k классифицировался с ошибкой, то , и, таким образом, можно записать следующее выражение:

Так как величина строго положительна, второй член будет по модулю превосходить третий при условии, что значение , до­статочно велико. В частности, если положить

(15)

и

(16)

то

и если выбрать

(17)

то получим следующее выражение:

Таким образом, квадрат расстояния от до при каждой коррек­ции будет уменьшаться, по крайней мере на величину , и послеk коррекций представится в следующем виде:

Поскольку величина квадрата расстояния не может быть отрица­тельной, из этого следует, что последовательность коррекций долж­на быть ограничена числом коррекций, не большим чем k₀, где

(18)

Поскольку коррекция осуществляется всякий раз, когда выборка классифицируется с ошибкой, и поскольку каждая выборка появ­ляется бесконечно большое число раз в последовательности, отсюда следует, что после прекращения процесса коррекций полученный весовой вектор должен правильно осуществлять классификацию всех выборок.

Число k₀ определяет предельное значение числа коррекций. Если a₁=0, получается следующее достаточно простое выражение для k₀:

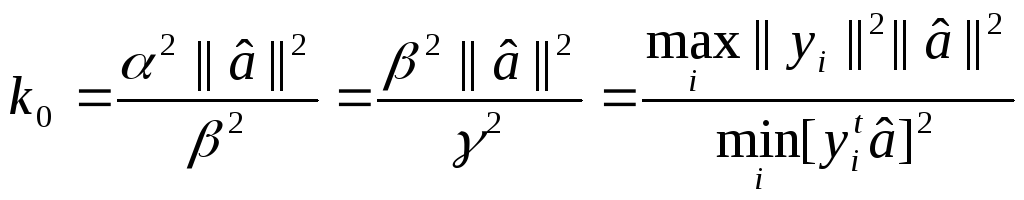(19)

Данное выражение показывает, что трудность задачи в основном определяется наличием выборок, наиболее близких к ортогональным по отношению к вектору решения. К сожалению, указанное выражение невозможно использовать при рассмотрении нерешенной задачи, поскольку в данном случае граница должна определяться исходя из неизвестного вектора решения. Очевидно, что в общем случае задачи с линейно разделяемыми множествами могут пред­ставлять известные трудности для определения решения в условиях компланарности выборок. Тем не менее, если выборки линейно разделяемы, правило постоянного приращения будет давать реше­ние после конечного числа коррекций.