5.8.2. Связь с линейным дискриминантом Фишера

В данном пункте будет показано, что при соответствующем выборе вектора b функция а^tу, найденная по методу минимальной квадратичной ошибки, непосредственно связана с линейным дискриминантом Фишера. Для того чтобы показать это, следует вернуться к необобщенным линейным разделяющим функциям. Предположим множество п d-мерных выборок x₁,…x_n принадлежат подмножеству X₁, помеченному ₁, а n₂ – подмножеству X₂ помеченному ₂. Далее положим, что выборка y_i образуется из х_i, путем прибавления порогового компонента, и умножением полученного вектора на –1 в случае выборки, помеченной ₂. Не нарушая общности,

можно положить, что первыеn₁ выборок помечены ₁, а последующие n₂помечены ₁. Тогда матрицу Y можно представить в следующем виде:

где u_i является вектор столбцов из n_i компонент, а Х_i – матрицей размера n_i×d, строками которой являются выборки, помеченные _i. Соответствующим образом разложим a и b:

и

Можно показать, что при определенном выборе b обнаруживается связь между решением по методу наименьшей квадратичной ошибки и линейным дискриминантом Фишера.

Доказательство начнем, записав соотношение (32) для а с использованием разложенных матриц:

Определяя выборочное среднее m_i, и матрицу суммарного выборочного разброса S_W:

можно в результате перемножения матриц, входящих в (36), получить следующее выражение:

Полученное выражение может рассматриваться как пара уравнений, причем из первого можно выразить w₀ через w:

где m является средним по всем выборкам. Подставив данное выражение во второе уравнение, и выполнив некоторые алгебраические преобразования, получим

Поскольку направление вектора (m₁ – m₂)(m₁ m₂)^t w при любом w совпадает с направлением вектора m₁ – m_2, то можно записатьследующее выражение:

где α — некоторая скалярная величина. В этом случае соотношение (40) дает

что, за исключением скалярного коэффициента, идентично решению для случая линейного дискриминанта Фишера. Помимо этого, получаем величину порогаw₀ и следующее решающее правило: принять решение ω₁, если w^t(x - m)>0; иначе принять решение ω₂.

5.8.3. Асимптотическое приближение к оптимальному дискриминанту

Другое свойство решения по методу наименьшей квадратичной ошибки, говорящее в его пользу, состоит в том, что при условии b=u_n и при п→∞ оно в пределе приближается в смысле минимума среднеквадратичной ошибки к разделяющей функции Байеса

Чтобы продемонстрировать данное утверждение, следует предположить, что выборки взяты независимо в соответствии с вероятностным законом

Решение по методу наименьшей квадратичной ошибки с использованием расширенного вектораy дает разложение в ряд функции g(x)=a^ty, где у=у(х). Если определить среднеквадратичную ошибку аппроксимации выражением

то нашей задачей будет показать, что величина ε² минимизируется посредством решения а=Y^† u_n.

Доказательство упростится при условии сохранения различия между выборками класса 1 и класса 2. Исходя из ненормированных данных, функцию критерия J_s можно записать в виде

Таким образом, в соответствии с законом больших чисел при стремлениип к бесконечности (1/n)J_S(а) приближается с вероятностью 1 к функции (а), имеющей вид

Т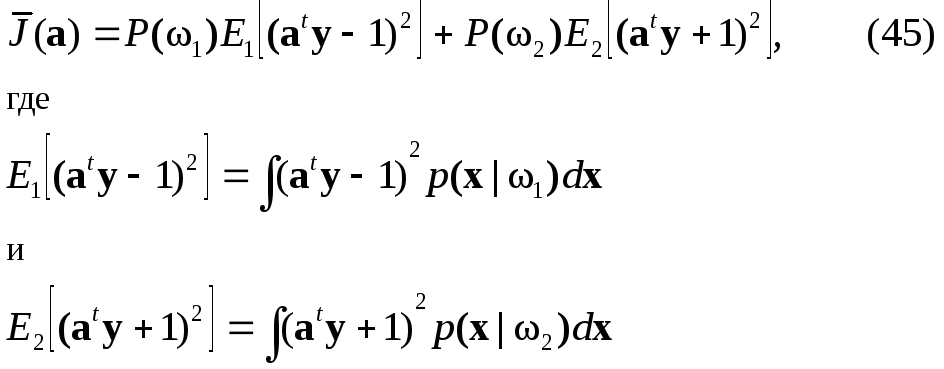еперь, если мы из соотношения (42) определим

Второй член данной суммы не зависит от весового вектора а. Отсюда следует, что а, которое минимизирует J_S , также минимизирует и ε² — среднеквадратичную ошибку между а^tу и g_o(x).

Данный результат позволяет глубже проникнуть в суть процедуры, обеспечивающей решение по методу наименьшей квадратичной ошибки. Аппроксимируя g_o(x), разделяющая функция а^tу дает непосредственную информацию относительно апостериорных вероятностей P(ω₁|x)= 1/2(1+g_o) и P(ω₂|x)= 1/2 (1-g_o). Качество аппроксимации зависит от функций у_i(х) и числа членов в разложении а^tу. К сожалению, критерий среднеквадратичной ошибки в основном распространяется не на точки, близкие к поверхности решения g_o(x)=0, а на точки, для которых значение р(х) велико. Таким образом, разделяющая функция, которая наилучшим образом аппроксимирует разделяющую функцию Байеса, не обязательно минимизирует вероятность ошибки. Несмотря на данный недостаток, решение по методу наименьшей квадратичной ошибки обладает интересными свойствами и широко распространено в литературе. Далее, при рассмотрении методов стохастической аппроксимации, еще предстоит встретиться с задачей среднеквадратичной аппроксимации функции g_o(x).