Общие
положения
|
Токи,
напряжения и ЭДС, значения которых
периодически изменяются во времени
по синусоидальному закону, называют
синусоидальными (гармоническими).
По сравнению с постоянным током
синусоидальный имеет ряд преимуществ.
В частности, производство, передача
и использование электрической
энергии наиболее экономичны при
синусоидальном токе; в цепях
синусоидального тока относительно
просто преобразовывать форму
напряжения, а также создавать
трехфазные системы напряжения.
Синусоидальные токи широко используют
в радио-, связной и контрольно-измерительной
технике и в других областях.
В
зависимости от типа решаемой задачи
синусоидальные величины представляют:
|
|
Аналитическое
представление синусоидальных величин
|
Синусоидальные
ЭДС, напряжение и ток можно задать
с помощью вещественных
функций времени
(в виде аналитических выражений):
e(t)
= Emsin(t
+ e);
u(t)
= Umsin(t
+ u);
i(t)
= Imsin(t
+ i),
|
(3.1)
|
где
е,
u,
i
- соответственно мгновенные значения
ЭДС, напряжения, тока;
t+e,
t+u,
t+i
- аргументы (фазы) синусоидальных
функций.
Для
расчета электрических цепей
аналитические выражения синусоидальных
величин неудобны,
т. к. алгебраические действия
(сложение, вычитание, умножение и
т. д.) с тригонометрическими функциями
приводят к громоздким вычислениям.
|
|
Временная
диаграмма
|
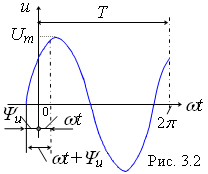
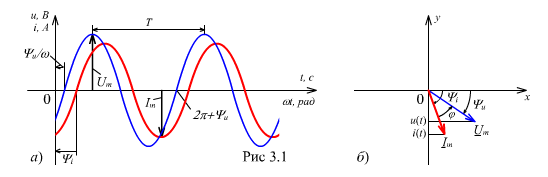
Графическое
представление синусоидальных
величин в виде временной диаграммы
(рис. 3.1, а)
достаточно наглядно, но из-за
сложности построения синусоид и
операций с ними применяется
сравнительно редко. При построении
временной диаграммы за аргумент
синусоидальной функции, например,
напряжения u(t)
принимают время t
(чему соответствуют период T
и начальное время t0
= u
/ )
или угол t
(чему соответствуют период T
= 2
и начальная фаза u
в радианах) (см. рис. 3.1, а).
Однако для большей наглядности угол
u
часто выражают в градусах. Тогда
аргумент t
также переводят в градусы (напомним,
что 1 рад
57,3).
В этом случае период составляет
360.
|
|
Векторная
диаграмма
|
Представление
синусоидальных функций при помощи
векторов
(векторных диаграмм)
позволяет наглядно показать
количественные и фазовые соотношения
между электрическими величинами в
цепях синусоидального тока и широко
используется при анализе физических
процессов и выводе основных
соотношений.
Векторная
диаграмма
(ВД) - это совокупность векторов ЭДС,
напряжения и тока, изображающих на
плоскости синусоидально изменяющиеся
с одной и той же частотой величины.
В
прямоугольной системе координат
(оси x,
y)
векторы обозначают соответствующими
буквами, подчеркнутыми снизу: векторы
амплитуды ЭДС Em,
напряжения Um,
тока Im
и т.д. (рис. 3.1, б).
Длина, например, вектора амплитуды
тока Im
должен быть равна (в соответствующем
масштабе) амплитуде тока Im,
а угол наклона к оси абсцисс - его
начальной фазе i
. В этом случае проекция
вектора тока
Imsini
на ось ординат равна мгновенному
значению тока
в момент времени t
= 0, т. е. Im
sin i
(см. рис. 3.1, б).
Если гармонические колебания
напряжения и тока ветви
или на
входе цепи
имеют одну и ту же частоту ,
то соответствующие этим колебаниям
векторы Um
и Im
вращаются с одинаковой частотой
вокруг начала координат против
направления вращения часовой
стрелки. За время t
векторы Um
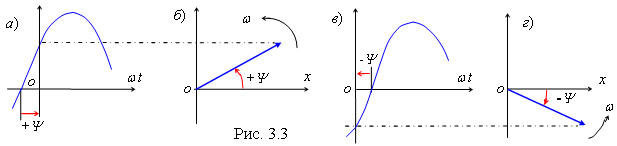
и Im
повернуться на угол t
относительно начального положения,
так что их углы наклона к оси абсцисс
станут равными (t+u)
и (t+i),
а проекции векторов Um
и Im
на ось ординат - u(t)
= Umsin(t
+ u)
и i(t)
= Imsin(t
+ i).
Однако, угол сдвига фаз
= u
-i
между ними (см. рис. 3.1, б)
остаётся неизменным, поэтому при
построении векторной диаграммы
векторы обычно изображают не
вращающимися, а неподвижными
для момента времени t
= 0 (t
= 0), т. к. взаимное расположение
векторов на плоскости зависит не
от фаз (начальных фаз), а от угла
сдвига фаз
.
Таким
образом, векторы
отображают синусоидальные функции,
а операции (сложение, вычитание и
т. д.) с векторами отображают
соответствующие операции с
синусоидальными функциями.
Отметим,
что неподвижные векторы определяют
два параметра синусоидальных
функций: амплитуды и начальные фазы.
Третий параметр - угловая частота
ω
- должен быть известен.
|
|
Основные
параметры синусоидальных величин
|
Для
характеристики синусоидальных
функций времени используют следующие
параметры:
|
-
Мгновенное значение;
-
Амплитуда;
-
Период;
-
Частота;
-
Фаза;
-
Начальная фаза;
-
Угловая частота;
-
Соотношение между T,
ω
и ƒ;
-
Сдвиг фаз;
-
Среднее значение гармонической
функции;
-
Действующее значение гармонической
функции.
|
|
|
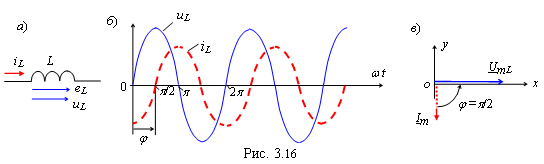
т.
е. ток
iL
в индуктивном элементе отстаёт от
напряжения uL
по фазе на угол
/2 (или напряжение uL
опережает по фазе ток iL
на угол
/2).
Реактивное
ёмкостное сопротивление конденсатора
|
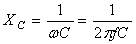 -
-
|
(3.42)
|
-
реактивное ёмкостное сопротивление,
обратно пропорциональное частоте
ω.
При частоте ω
= 0 (постоянный ток) ёмкостное
сопротивление XC
->
∞,
т. е. ветвь с ёмкостным элементом
при постоянном токе как бы разомкнута
(ток в ней равен нулю), а при частоте
ω
∞
ёмкостное сопротивление XC
0.
|
|
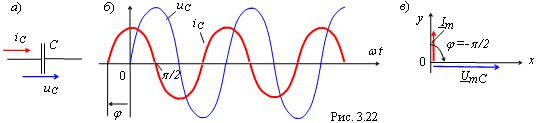
Угол
сдвига фаз между напряжением и током
конденсатора
|
Сдвиг
фаз между напряжением uC(t)
и током iC(t)
в ёмкостном элементе (рис. 3.22, а)
 <>
<>

|
(3.43)
|
т.
е. ток iC(t)
в ёмкостном элементе опережает
напряжение uC(t)
по фазе на угол π/2
(рис. 3.22, б
и в).
|
|
3.4.1.
Мгновенная мощность цепи гармонического
тока
|
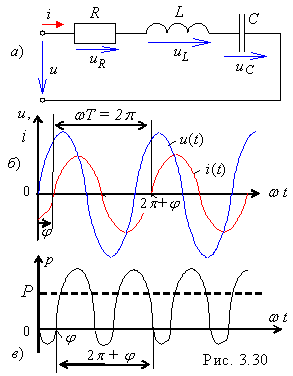
При
гармоническом напряжении
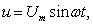 приложенном
к зажимам RLC-цепи
(рис. 3.30, а),
и установившемся в ней токе
приложенном
к зажимам RLC-цепи
(рис. 3.30, а),
и установившемся в ней токе
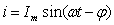
Проведём
анализ каждой составляющей мощности
р(t)
цепи.
|
|
Активная
мощность цепи гармонического тока
|
А нализируя
мгновенную мощность
нализируя
мгновенную мощность
 (рис.
3.31, а)
в резистивном
элементе R,
т. е.
(рис.
3.31, а)
в резистивном
элементе R,
т. е.
 ,
замечаем, что она знакоположительная
функция. Это означает, что электрическая
энергия источника необратимо
преобразуется в элементе R
в тепловую энергию. Такую мощность
называют активной
и измеряют в ваттах [Вт].
,
замечаем, что она знакоположительная
функция. Это означает, что электрическая
энергия источника необратимо
преобразуется в элементе R
в тепловую энергию. Такую мощность
называют активной
и измеряют в ваттах [Вт].
Степень
необратимого преобразования энергии
оценивают средним значением
мгновенной мощности р(t)
за период T
и обозначают буквой P:

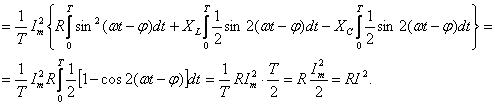 С
другой стороны (см. (3.54))
С
другой стороны (см. (3.54))
 Примечание.
Напомним, что интеграл от гармонических
функций sint,
cost,
cos2t,
cos(t-),
cos(2t-)
и т. д. за период Т
равен нулю.
Примечание.
Напомним, что интеграл от гармонических
функций sint,
cost,
cos2t,
cos(t-),
cos(2t-)
и т. д. за период Т
равен нулю.
Итак,
активная
мощность цепи синусоидального
тока есть среднее значение общей
мощности р(t)
за период T.
Она равна произведению действующих
значений приложенного к цепи
напряжения U
и тока I,
умноженному на
cosφ,
т. е.
P
= UI
cosφ
= RI2.
|
(3.55)
|
|
|
Реактивная
индуктивная мощность цепи гармонического
тока
|
Анализ
мгновенной мощности в индуктивном
элементе L
 п
п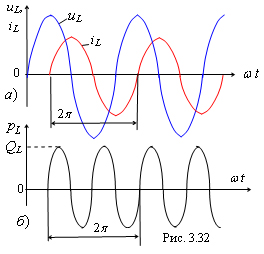 оказывает,
что это знакопеременная функция,
изменяющаяся с двойной частотой по
отношению к частоте изменения
напряжения uL
и тока iL
в цепи (рис. 3.32, б).
Среднее значение мощности
оказывает,
что это знакопеременная функция,
изменяющаяся с двойной частотой по
отношению к частоте изменения
напряжения uL
и тока iL
в цепи (рис. 3.32, б).
Среднее значение мощности
 за
период T
равно
нулю.
за
период T
равно
нулю.
В
индуктивном
элементе в первую четверть периода
T
(см. рис. 3.32, а)
напряжение uL
и ток iL
имеют знак плюс, поэтому мощность
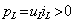 ,
т. е. индуктивный элемент потребляет
электрическую энергию источника и
преобразовывает её в магнитную,
накапливая её в магнитном поле
катушки. Во вторую четверть периода
напряжение uL
и ток iL
имеют противоположные знаки, поэтому
мощность
,
т. е. индуктивный элемент потребляет
электрическую энергию источника и
преобразовывает её в магнитную,
накапливая её в магнитном поле
катушки. Во вторую четверть периода
напряжение uL
и ток iL
имеют противоположные знаки, поэтому
мощность
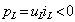 .
В это время накопленная магнитная
энергия возвращается источнику,
преобразовываясь в электрическую
энергию. В третьей четверти происходит
накопление энергии в магнитном поле
элемента L,
в четвертой - её возврат источнику
энергии.
.
В это время накопленная магнитная
энергия возвращается источнику,
преобразовываясь в электрическую
энергию. В третьей четверти происходит
накопление энергии в магнитном поле
элемента L,
в четвертой - её возврат источнику
энергии.
Интенсивность
преобразования электрической
энергии источника в магнитную в
элементе L
и наоборот оценивается реактивной
индуктивной мощностью +QL,
которая равна амплитуде мощности
рL
(см. рис. 3.32, б),
всегда берётся со знаком плюс и
измеряется в варах (вольт-ампер
реактивный),
т. е.
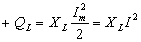 ,
вар.
,
вар.
|
(3.56)
|
|
|
Соотношение
между комплексной и временной функциями
|
Воспользовавшись
формулой Эйлера, запишем комплекс
амплитуды напряжения в тригонометрической
форме (рис. 3.9, б):
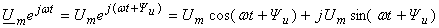 .
.
|
(3.10)
|
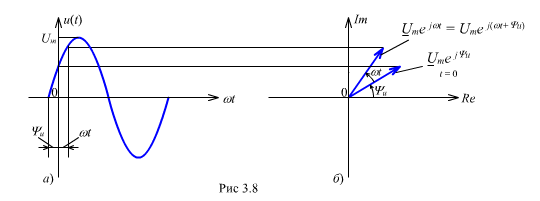
Соотношение
(3.10) показывает, что синусоидальная
функция напряжения u(t)
= Umsin(ωt
+ u)
есть проекция
вращающегося вектора на мнимую ось,
или есть мнимая часть (без j)
комплексной амплитуды напряжения,
т. к.
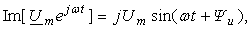
|
(3.11)
|
а
косинусоидальная
функция напряжения u(t)
= Umcos(ωt
+ u)
есть проекция
вращающегося вектора на действительную
ось,
или действительная часть комплексной
амплитуды напряжения, т. к.
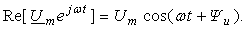
|
(3.12)
|
Например,
u
= 10 sin(ωt
+ 45°)
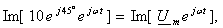 где
где
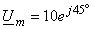 -
комплексная
амплитуда
напряжения.
-
комплексная
амплитуда
напряжения.
|
|
Комплекс
напряжения (тока)
|
Поделив
комплексную амплитуду напряжения
на
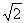 ,
получим комплекс действующего
значения напряжения или комплекс
напряжения:
,
получим комплекс действующего
значения напряжения или комплекс
напряжения:

|
(3.13)
|
По
аналогии запишем комплекс тока
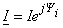 и
комплекс ЭДС
и
комплекс ЭДС
 .
.
Например,
ток i
= 14,1sin(314 t
- 30°) А
 A.
A.
|
|
Переход
от комплексов к временным функциям
|
Как
можно заметить, обратный переход
от комплексов к синусоидальным
функциям осуществляют следующим
образом:
 u(t)
=
Usin(ωt
+ u);
u(t)
=
Usin(ωt
+ u);
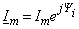 i(t)
= Imsin(t
+ Ψi)
и
т.
д.
i(t)
= Imsin(t
+ Ψi)
и
т.
д.
|
|
|
Свойства
комплексных чисел
Расчёт электрических
цепей комплексным методом проводят
с использованием алгебры
комплексных чисел.
Рассмотрим некоторые соотношения
алгебры комплексных чисел.
Три
формы записи комплексного числа
|
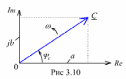
Аналитически
комплексное число С
можно представить в алгебраической,
тригонометрической и показательной
формах (рис. 3.10):
 С
= a + jb
- алгебраическая,
С
= Cejc-
показательная,
С
= C(cosc
+ jsinc)
- тригонометрическая
формы,
т. е.
С
= a + jb
- алгебраическая,
С
= Cejc-
показательная,
С
= C(cosc
+ jsinc)
- тригонометрическая
формы,
т. е.
|
С
= Cejc
= C (cosc
+ jsinc)
= a + jb,
|
(3.15)
|
где
С
= |C|=
 -
модуль
комплексного числа С;
c
= arctg
-
модуль
комплексного числа С;
c
= arctg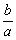 - аргумент
комплексного числа С;
a
= Re[C]
- действительная часть; b
= Im[C]
- мнимая часть комплексного числа
С.
- аргумент
комплексного числа С;
a
= Re[C]
- действительная часть; b
= Im[C]
- мнимая часть комплексного числа
С.
Если
модуль С
= 1, то получим формулу
Эйлера:
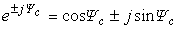 .
.
|
|
|
Обозначения
комплексных величин
|
Согласно
ГОСТу 2-710-81 любая комплексная
величина обозначается
соответствующей буквой с чертой
под ней, например, С,
U,
E,
I.
Мы будем придерживаться этого
обозначения. Заметим, что по
ГОСТу для синусоидально
изменяющихся величин, таких как
напряжение, ток и т. д., разрешается
обозначать их комплексы
соответствующей буквой с точкой
над ней:
 ,
,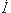 ,
,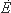 и т. д. Записи
и
U;
I
и
и
т. д. эквивалентны.
и т. д. Записи
и
U;
I
и
и
т. д. эквивалентны.
|
|
Переход
от одной формы записи к другой
|
В
соответствии с уравнением (3.15)
переход от алгебраической
формы С
= a ±
jb
к
показательной
осуществляют
по формуле:
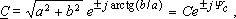
|
(3.16)
|
а
от показательной
формы к
алгебраической
-
через тригонометрическую:
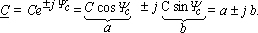
|
(3.17)
|
Примечание.
Если
действительная часть комплексного
числа имеет знак минус, например,
комплекс C
= - a ±
jb,
то его аргумент
определяют
по формуле: с
= ±
arctg(b/a)
± .
Например,
 ;
;
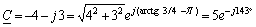 .
.
|
|
Сложение
и вычитание комплексных чисел
|
Сложение
и вычитание комплексных чисел
удобно проводить в алгебраической
форме, например,
A
±
B
= (a1
± ja2)
± (b1
± jb2)
=
(a1
± b1)
± j
(a2
± b2).
|
(3.18)
|
Чтобы
сложить два комплексных числа,
заданных в показательной форме,
например,
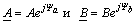 ,
вначале их нужно преобразовать
в алгебраическую форму согласно
(3.17), а затем использовать
соотношение (3.18).
,
вначале их нужно преобразовать
в алгебраическую форму согласно
(3.17), а затем использовать
соотношение (3.18).
|
|
Умножение
и деление комплексных чисел
|
Умножение
и деление комплексных чисел
удобно проводить в показательной
форме:
-
при умножении комплексов A
и B
их модули перемножают, a аргументы
суммируют:
 ;
;
|
(3.19)
|
-
при делении комплексов A
и B
их модули делят, а аргументы
вычитают:
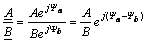 .
.
|
|
|
Умножение
комплекса на j,
j2,
...
|
Если
комплекс B
= Bejb=
1 · ej/2
( B
= 1, b
=
/2 ), то умножение вектора А
на
вектор B
,
т.е.
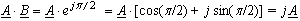
р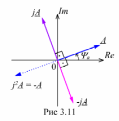 авнозначно
повороту вектора А
на
угол
/2 в
положительном направлении
(ejπ/2
= j -
оператор
поворота
на угол
/2), а умножение вектора А
на
оператор
-j
= e-jπ/2
равносильно его повороту на
угол
/2
по ходу часовой стрелки (см.
вектор -
jA
на
рис. 3.11).
авнозначно
повороту вектора А
на
угол
/2 в
положительном направлении
(ejπ/2
= j -
оператор
поворота
на угол
/2), а умножение вектора А
на
оператор
-j
= e-jπ/2
равносильно его повороту на
угол
/2
по ходу часовой стрелки (см.
вектор -
jA
на
рис. 3.11).
Умножив
вектор A
на оператор j2
= -1, получим
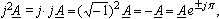 что
равносильно повороту вектора
А
на
угол ±π.
что
равносильно повороту вектора
А
на
угол ±π.
Вектор
-A
= Ae±jπ
имеет направление, противоположное
направлению вектора А
(см.
рис. 3.11).
|
|
Комплексно-сопряженные
числа
|
Если
комплексная величина
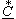 (рис.
3.12) отличается от комплекса С
только
знаком мнимой части, то она
называется сопряженным
комплексом (зеркальное отображение
вектора С
относительно
оси действительных чисел Re).
Итак, если C
= Cejc
= C (cosc
+ jsinc)
= a + jb,
то
(рис.
3.12) отличается от комплекса С
только
знаком мнимой части, то она
называется сопряженным
комплексом (зеркальное отображение
вектора С
относительно
оси действительных чисел Re).
Итак, если C
= Cejc
= C (cosc
+ jsinc)
= a + jb,
то
=
Ce-jc
= C (cosc
- jsinc)
= a - jb.
|
(3.21)
|

Произведение
комплексно-сопряженных
чисел
C
·
=
Cejc
· Ce-jc
= C2ej0
= C2
|
(3.22)
|
есть
действительное число, равное
квадрату С2
их модуля С
= |C|.
Это
свойство используют, например,
при делении комплексных чисел
в алгебраической форме: умножая
числитель и знаменатель на
сопряжённый комплекс знаменателя,
получают ответ в алгебраической
форме:
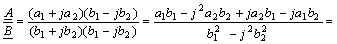
 .
.
|
(3.23)
|
Такую
форму умножения и деления
комплексных чисел часто применяют
при написании программ для ЭВМ.
|
|
|
|
Дифференцирование
и интегрирование комплексных функций
|
Запишем
гармонический ток i(t),
его производную и интеграл по времени
во временной области и их мгновенные
комплексы в комплексной плоскости:
временная
область
(функции
времени):
|
область
комплексного переменного
jω
(комплексные
функции времени)
|
функция
тока
i(t)
= Im
sin(ωt
+ i)
|
|
I(jω)
= Imej(ωt+i)
= Imejωt;
|
(3.25)
|
производная
функции тока
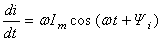 =
=
=
ω Im sin(ωt
+ i
+ /2)
|
|
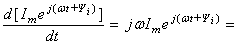
=
jωImejωt,
|
(3.26)
|
т.
е. производная
комплексной функции тока равна
комплексу тока, умноженной на jω.
Так как j
= ej/2,
то операция дифференцирования
комплекса функции тока приводит к
увеличению его модуля в ω
раз и повороту вектора в комплексной
плоскости на угол /2
в положительном направлении;
интеграл
функции тока
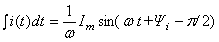
|
|
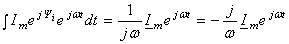 ,
,
|
(3.27)
|
т.
е. операция
интегрирования комплекса тока
соответствует его делению на ω
и повороту вектора в комплексной
плоскости по ходу часовой стрелки
на угол /2.
Полученные
соотношения будут использованы при
выводе компонентных уравнений
пассивных элементов электрических
цепей и при изображении векторных
диаграмм напряжений и токов в
комплексной плоскости.
|
|
Комплексный
(символический) метод
|
При
анализе установившихся процессов
в сложной электрической цепи
гармонические
функции изображают комплексными
числами,
что позволяет перейти от
интегрально-дифференциальных
уравнений, составленных для мгновенных
значений токов и ЭДС, к алгебраическим
уравнениям,
составленным для комплексов токов
и ЭДС.
При
этом комплексными числами изображаются
не только гармонические ЭДС, токи
и напряжения, но и параметры R,
L
и C
цепи. Решив систему комплексных
алгебраических уравнений, составленных
на основании законов Кирхгофа,
метода узловых напряжений, метода
контурных токов и др., рассмотренных
при анализе цепей постоянного тока,
находят комплексные
амплитуды (или
комплексные действующие значения)
токов или напряжений ветвей цепи.
Этот
метод называют также методом
комплексных амплитуд или
символическим
потому,
что мгновенные токи и напряжения
заменяют их комплексными изображениями
или символами
|
|
Преимущества
комплексного метода
|
Широкое
применение комплексного метода
расчёта цепей синусоидального тока
в установившихся режимах объясняется
следующими соображениями:
а)
метод предельно формализован, что
упрощает расчёт электрических цепей
гармонического тока сложной
конфигурации;
б) рассмотренные
в теме 2 методы расчёта цепей
постоянного тока (ЗК, МУН, МКТ, МЭГ
и др.) применимы к расчёту цепей
синусоидального тока комплексным
методом. По внешним признакам они
очень схожи: сохраняются все правила
составления систем уравнений, однако
при их записи посредством комплексных
чисел используют комплексные
сопротивления Zk
ветвей цепи (вместо сопротивлений
Rk),
а вместо электрических величин (ЭДС
E,
напряжения U,
тока I)
- их комплексы: E,
U,
I;
в)
посредством комплексного метода
рассчитывают частотные зависимости
(характеристики) электрических
величин.
|
|
Компонентные
уравнения пассивных элементов
электрической цепи в комплексной
форме
|
Пассивный
элемент электрической
цепи характеризуется своим комплексным
сопротивлением
Zэ
= Zэejφ
- комплексным числом, равным отношению
комплексного напряжения на зажимах
данного элемента к комплексному
току этого элемента при t
=
0, т. е.
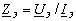
|
(3.64)
|
В
табл. 7.2…табл. 7.4 приведены компонентные
уравнения и комплексные сопротивления
элементов R,
L
и
С
.
Для сравнения в таблицах приведена
также запись компонентных уравнений
пассивных элементов для схем
замещения во временной области.
|
|
Таблица
3.2
|
Компонентное
уравнение и сопротивление элемента
R
в
комплексной форме
Для
схем замещения электрических
цепей во временной области:
|
Для
комплексных схем замещения
электрических цепей:
|

|
Условное
обозначение резистивного элемента
R
|
Мгновенные
значения тока и напряжения
|
Комплексные
ток и напряжение
|
iR
= Imsin(ωt+
i)
|
|
IR(ω)
=
Ie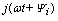
|
uR
= Umsin(ωt+
u)
|
|
UR(jω)=URe
|
Сопротивление
|
Комплексное
сопротивление
|
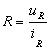
|
|
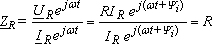
|
Компонентное
уравнение для мгновенных значений
|
Компонентное
уравнение в комплексной форме
|
uR
=
RiR
|
|
UR
= RIR
|
|
|
Таблица
3.3
|
Компонентное
уравнение и сопротивление элемента
L
в
комплексной форме
Для
схем замещения электрических
цепей во временной области
|
Для
комплексных схем замещения
электрических цепей
|
Условное
обозначение индуктивного элемента
L
|

|
Мгновенные
значения тока и напряжения
|
Комплексные
ток и напряжение
|
iL
= ImLsin(ωt+
i)
|
|
IL(jω)
=
ILejωt
|
uL
= L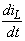 = ωLImsin(ωt
+ i+
90°)
= ωLImsin(ωt
+ i+
90°)
|
|
UL(jω)
=
= ULe
|
Индуктивность
|
Комплексное
сопротивление
|
L
|
|
ZL
= UL/IL
= jωL
= jXL
|
Компонентное
уравнение для мгновенных значений
|
Компонентное
уравнение в комплексной форме
|
uL
= L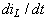
|
|
UL
= jXLIL
|
|
|
Комплексная
мощность
|
Комплексной
мощностью цепи называют комплексное
число S,
модуль которого равен полной мощности
S
цепи,
а аргумент - углу сдвига фаз φ
между
током и напряжением на её входе:
Переходя
от показательной формы записи S
к
тригонометрической S
= Scosφ
+ jSsinφ
,
устанавливаем, что действительная
часть комплексной мощности равна
активной
мощности цепи
Р
= Re[S]
= Scosφ.
|
(3.82)
|
Мнимая
часть комплексной мощности S
представляет
собой реактивную
мощность цепи
Q
=
Im[S]
= Ssinφ.
|
(3.83)
|
С
учетом (3.82) и (3.83) выражение (3.81) можно
записать следующим образом:
S
= P + jQ.
Следовательно,
комплексная
мощность S
представляет собой комплексное
число, действительная часть которого
равна активной мощности цепи P, а
мнимая - реактивной Q,
причем если имеем перед символом j
знак
минус, то это реактивная ёмкостная
мощность
- QС,
а если знак плюс - реактивная
индуктивная
мощность
+ QL.
|
|
Выражение
комплексной мощности через комплексы
напряжения и тока на зажимах цепи
|
В
§3.4.1 найдены выражения мощностей
участка цепи с током i
=
Imsin(ωt
+
i)
и напряжением на зажимах u
=
Umsin(ωt
+
u):
P
= UIcos(u
- i)
= UIcosφ
[Bт];
Q
= UIsin(u
- i)
=
UIsinφ
[вар];
S
= UI =
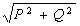 [B·A];
φ
= u
- i.
[B·A];
φ
= u
- i.
|
(3.84)
|
Подставив
в (3.81) выражения (3.84), получим
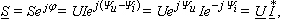
|
(3.85)
|
где
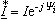 -
комплексно-сопряжённый
ток.
-
комплексно-сопряжённый
ток.
Таким
образом, комплексная
мощность цепи равна произведению
комплексного напряжения цепи U
на комплексно-сопряженный ток
 :
:
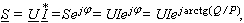
|
(3.86)
|
где
S
= UI - полная
мощность цепи.
|
|
Треугольник
мощностей
|
Комплексному
числу S
можно
поставить в соответствие отрезок
S,
проекции которого на оси действительных
и мнимых чисел равны Р
и Q.
Прямоугольный
треугольник с гипотенузой, равной
S, и катетами Р и Q называют
треугольник мощностей
(рис. 3.60).
К оэффициент
мощности cosφ = P/S
(φ = arctgQ/P) характеризует
степень приближения активной
мощности нагрузки к максимальному
значению, равному полной мощности
S = UI источника энергии.
Очевидно, что наивысшее значение
(cosφ = 1) коэффициент мощности
имеет при чисто активном характере
нагрузки.
оэффициент
мощности cosφ = P/S
(φ = arctgQ/P) характеризует
степень приближения активной
мощности нагрузки к максимальному
значению, равному полной мощности
S = UI источника энергии.
Очевидно, что наивысшее значение
(cosφ = 1) коэффициент мощности
имеет при чисто активном характере
нагрузки.
|
|





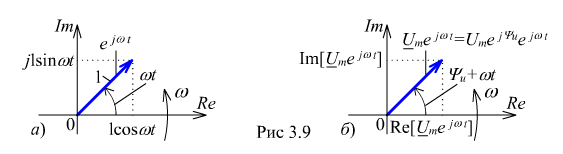



 <>
<>
 нализируя
мгновенную мощность
нализируя
мгновенную мощность

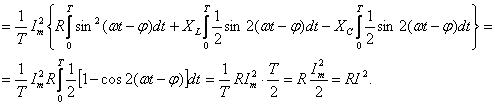 С
другой стороны (см. (3.54))
С
другой стороны (см. (3.54)) Примечание.
Напомним, что интеграл от гармонических
функций sint,
cost,
cos2t,
cos(t-),
cos(2t-)
и т. д. за период Т
равен нулю.
Примечание.
Напомним, что интеграл от гармонических
функций sint,
cost,
cos2t,
cos(t-),
cos(2t-)
и т. д. за период Т
равен нулю.
 оказывает,
что это знакопеременная функция,
изменяющаяся с двойной частотой по
отношению к частоте изменения
напряжения uL
и тока iL
в цепи (рис. 3.32, б).
Среднее значение мощности
оказывает,
что это знакопеременная функция,
изменяющаяся с двойной частотой по
отношению к частоте изменения
напряжения uL
и тока iL
в цепи (рис. 3.32, б).
Среднее значение мощности
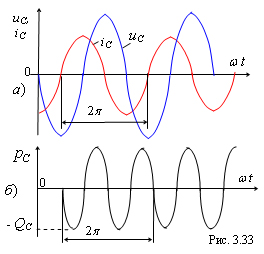 нализируя
мгновенную мощность в ёмкостном
элементе
нализируя
мгновенную мощность в ёмкостном
элементе
 заключаем,
что это знакопеременная функция
времени (рис. 3.33, б),
изменяющаяся с частотой 2
и находящаяся в противофазе с
реактивной индуктивной мощностью
рL(t)
(см. рис. 3.32, б).
заключаем,
что это знакопеременная функция
времени (рис. 3.33, б),
изменяющаяся с частотой 2
и находящаяся в противофазе с
реактивной индуктивной мощностью
рL(t)
(см. рис. 3.32, б).
 С
= a + jb
- алгебраическая,
С
= Cejc-
показательная,
С
= C(cosc
+ jsinc)
- тригонометрическая
формы,
т. е.
С
= a + jb
- алгебраическая,
С
= Cejc-
показательная,
С
= C(cosc
+ jsinc)
- тригонометрическая
формы,
т. е.

 авнозначно
повороту вектора А
на
угол
/2 в
положительном направлении
(ejπ/2
= j -
оператор
поворота
на угол
/2), а умножение вектора А
на
оператор
-j
= e-jπ/2
равносильно его повороту на
угол
/2
по ходу часовой стрелки (см.
вектор -
jA
на
рис. 3.11).
авнозначно
повороту вектора А
на
угол
/2 в
положительном направлении
(ejπ/2
= j -
оператор
поворота
на угол
/2), а умножение вектора А
на
оператор
-j
= e-jπ/2
равносильно его повороту на
угол
/2
по ходу часовой стрелки (см.
вектор -
jA
на
рис. 3.11).

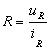


 оэффициент
мощности cosφ = P/S
(φ = arctgQ/P) характеризует
степень приближения активной
мощности нагрузки к максимальному
значению, равному полной мощности
S = UI источника энергии.
Очевидно, что наивысшее значение
(cosφ = 1) коэффициент мощности
имеет при чисто активном характере
нагрузки.
оэффициент
мощности cosφ = P/S
(φ = arctgQ/P) характеризует
степень приближения активной
мощности нагрузки к максимальному
значению, равному полной мощности
S = UI источника энергии.
Очевидно, что наивысшее значение
(cosφ = 1) коэффициент мощности
имеет при чисто активном характере
нагрузки.