Поток теплоты на единицу длины цилиндров

.

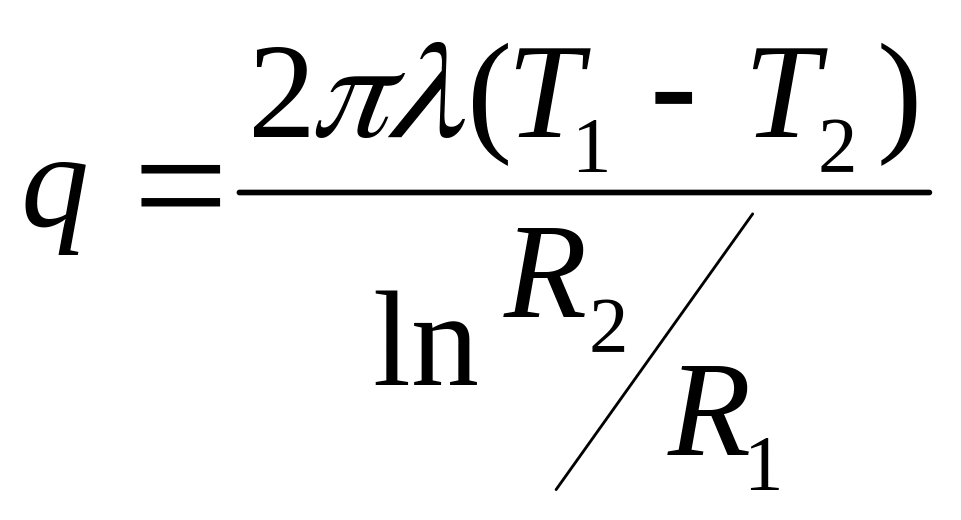2.17. Горизонтально расположенный диск радиусом R=0,1 м подвешен на тонкой упругой нити над таким же диском, укрепленным на вертикальной оси. Коэффициент кручения нити (отношение приложенного вращательного момента к углу закручивания) = 1,8 . Расстояние между дисками h = 0,1 м. Если нижний диск привести во вращение со скоростью 40 рад/с, верхний диск повернется на угол 70⁰. Определить вязкость воздуха. Закон изменения скорости слоев воздуха вдоль оси дисков считать линейным.

Решение.

При вращении нижнего диска прилегающий к нему слой воздуха вовлекается во вращательное движение. Вблизи поверхности диска воздух приобретает такую же линейную скорость, как и точки на поверхности диска. Вследствие внутреннего трения момент импульса передается слоям газа и, наконец, верхнему диску.

Выделим на верхнем диске кольцо площадью . Тогда сила, действующая на это кольцо со стороны прилегающего к нему слоя,

где F - сила вязкого трения, действующая на единичную площадку этого слоя:

.

-коэффициент вязкости.

Согласно условию задачи, .

где - скорость точек нижнего диска на расстоянии г от оси; k- неизвестный коэффициент.

Если верхний диск покоится, то V(h)= 0 , т.е. и k = .

Тогда градиент скорости

/

Подставляя выражение (3) в формулу (2), находим

/

Момент сил вязкого трения, действующих на выделенное кольцо диска,

.

Следовательно, момент сил вязкого трения, действующих со стороны воздуха на весь диск: .

Согласно закону Гука, момент упругой силы, действующей на диск со стороны нити, .

Находим теперь коэффициент вязкости:

.

2.18. Дана смесь газов, состоящая из неона, масса которого m₁ = 4 кг, и водорода, масса, которого m₂= 1 кг. Газы считать идеальными. Определить удельные теплоемкости смеси газов в процессах р = const, V=const.

Решение.

1) Удельные теплоемкости идеальных газов в процессах V=const и p=const определяются формулами

где i — число степеней свободы молекул, М — масса моля (или киломоля) газа.

Удельная теплоемкость смеси газов в данном процессе (например, р = const) складывается из удельных теплоемкостей в соответствующем процессе всех газов, входящих в эту смесь, с учетом их весового содержания в этой смеси. Найдем удельную теплоемкость смеси . По определению, «количество теплоты» dQ, сообщенное смеси, равно:

.

Где - удельная теплоемкость рассматриваемой| смеси идеальных газов.

С другой стороны, выражение для dQ можно записать

где и удельные теплоемкости массы неона и водорода соответственно, Сравнивая формулы (3) и (4), получим:

.

Отсюда: .

Или:

.

Обозначив и получим

.

К₁ и К₂ — коэффициенты, учитывающие весовое содержание соответствующих компонентов газов в смеси, или, другими словами, коэффициенты, по­казывающие, какую долю массы смеси составля­ет масса первого и второго газа.

Аналогичное выражение получим для удельной теплоемкости смеси газов в процессе p=const. .

2) В рассмотренном конкретном примере: не­он — одноатомный газ, следовательно, i₁ = 3; во­дород — двухатомный газ, следовательно, i₂=5. Используя формулу (7), учитывая (1) и (2), по­лучим:

.

Подстановка числовых значений дает: = 2,58-10³ Дж/кг-К.

Аналогично, согласно формуле (8), получим

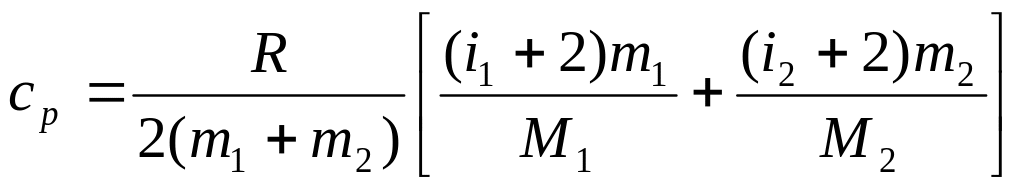=3,76 Дж/кгК .

2.19. Имеем некоторый идеальный двухатом­ный газ, разность его удельных теплоемкостей при постоянном давлении с_р и при постоянном объеме c_V равна 260 Дж/кг-К. Определить массу киломоля газа и его удельные теплоемкости с_р и с_V.

Решение.

Уравнение Р. Майера для удельных теплоемкостей запишется в виде

.

из него определим М: .

Разделив почленно уравнение (1) на с_р (или на с_V), получим

. и, приняв во внимание формулы

и

находим: .

Подставив числовые значения в соответствующую формулу, получим

М = = 32 кг/кмоль.

Газ но условию — двухатомный, М = 32, таким газом является кислород (О₂), для него: = 910 Дж/кг

=650 Дж/кг-К

2.20. Какая часть молекул парообразного йода диссоциирована на атомы при некоторой температуре Т, если удельная теплоемкость с_р, измеренная при этой температуре, оказалась 0,033 кал/г-град. Атомный вес йода 126,9. Решение.

Обозначим часть молекул, диссоциированных на атомы, . Эта часть молекул будет представлять собой одноатомный газ и соответственно обладать тремя степенями свободы, т. е i₁ =3. Число недиссоциированных молекул будет (1— ), и эта часть газа будет обладать соответственно пятью степенями свободы, (i₂ = 5 как идеальный двухатомный газ. Тогда, согласно формулам классической теории теплоемкости, - удельная теплоемкость газа с молекулярным весом М и числом степеней свободы i. В нашем случае имеется смесь газов и, согласно формуле (8), имеем:

.

Здесь коэффициенты К₁ и К₂ учитывают, какую долю смеси газов составляют соответственно первый (диссоциированный) и второй (недиссоциированный) газы.

В нашем случае : ,

Тогда: .

Имеем далее:

.

После несложных преобразований найдем, что

Откуда: .

2.21. Изменение состояния идеального газа происходит по политропе PVⁿ= const. Задана удельная теплоемкость с_р .

а) Найти выражение для удельной теплоемкости в политропическом процессе через показатель политропы и адиабаты.

Б) Разобрать частные случаи n=0, n= , n=1, n= и построить графики зависимости теплоемкости идеального газа от показателя политропы.

Решение.

1. Для политропического процесса 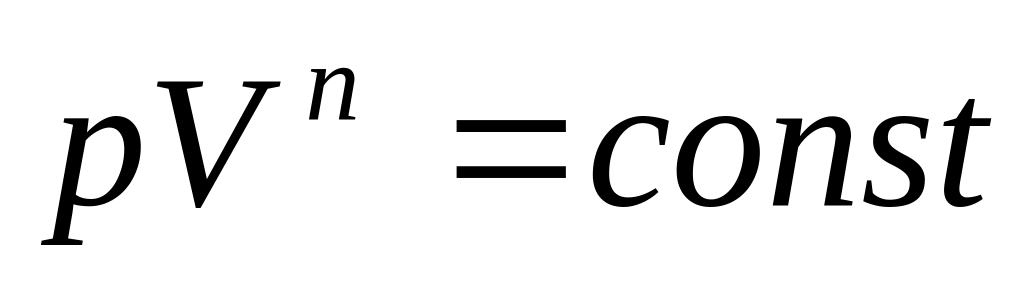Связь показателя политропы с теплоемкостью С определяется формулой 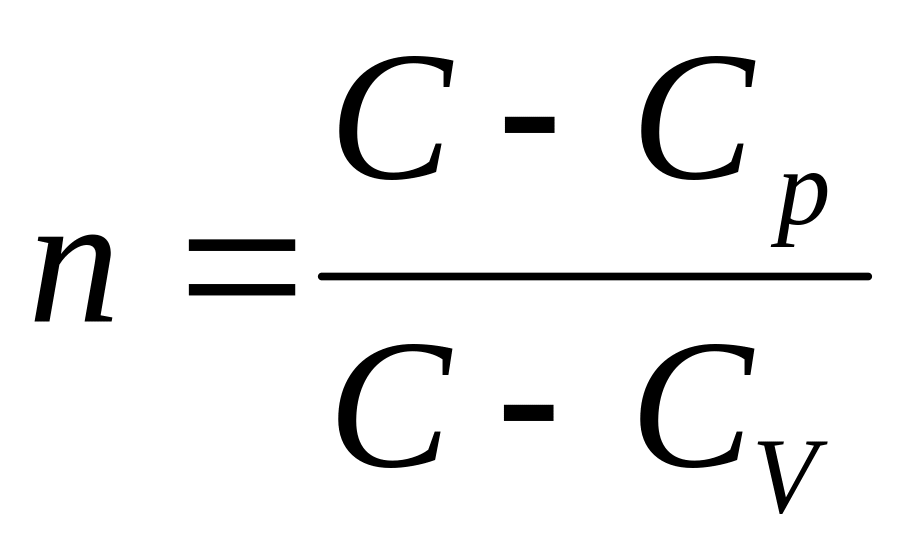. которая легко получается из уравнения состояния идеального газа и уравнения Р.Майера. Показатель адиабаты равен 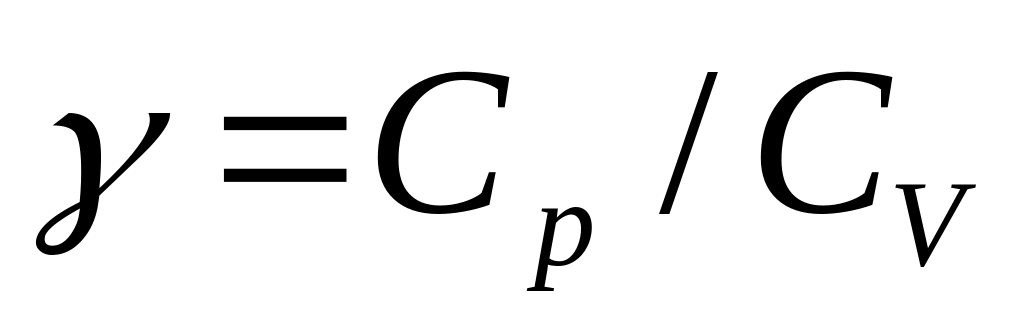. Можно теперь определить удельную теплоемкость .

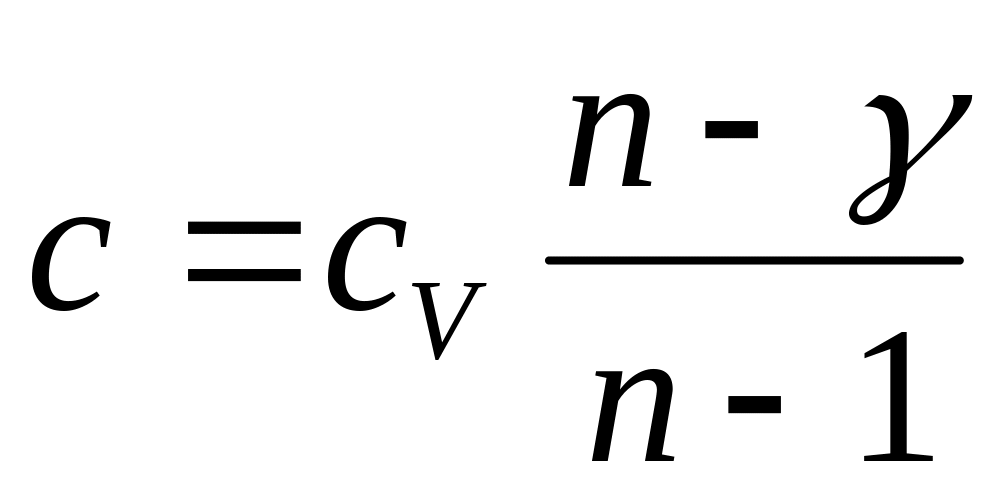2. Разберем частные случаи: а) n=0, тогда с=с_р, т.е. имеем изобарический процесс; б) 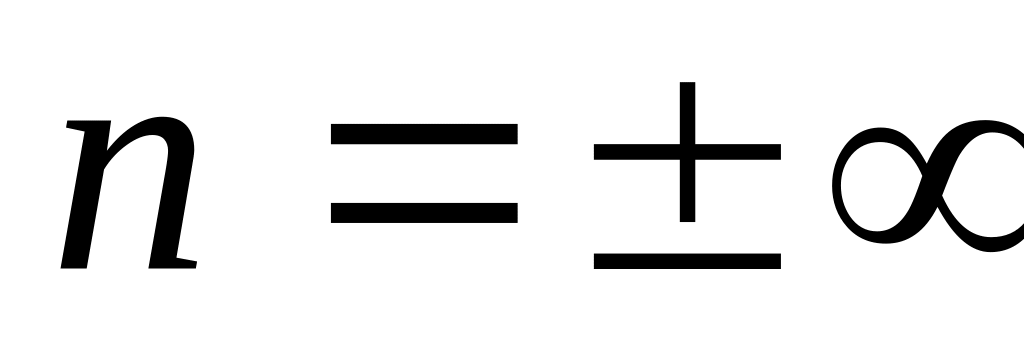, с=с_v – процесс изохорический; в) n=1, 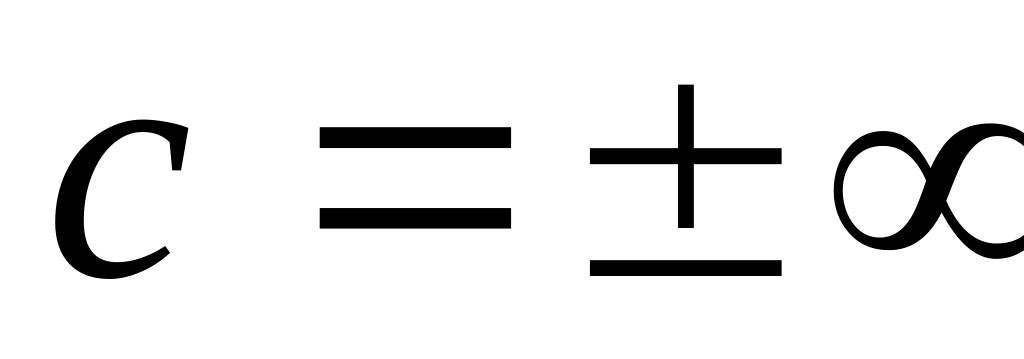, т.е. имеем изотермический процесс; г) , с=0 – адиабатный процесс.