Решение.

Подставив в уравнение Менделеева – Клапейрона P=b/Vⁿ, получим:

Выразим температуру из последнего уравнения:

Отсюда ясно, что если n<1, то при расширении газа температура увеличивается, если же n>1, температура уменьшается.

2.12. Давление воздуха внутри бутылки, закрытой пробкой, равно 0,1 МПа при температуре 7⁰С. На сколько градусов нужно нагреть воздух в бутылке, чтобы пробка вылетела? Без нагревания пробку можно вынуть, прикладывая к ней силу 30 Н. Сечение пробки 2 см².

Решение.

Чтобы пробка вылетела из бутылки, необходимо, чтобы давление воздуха в бутылке равнялось:

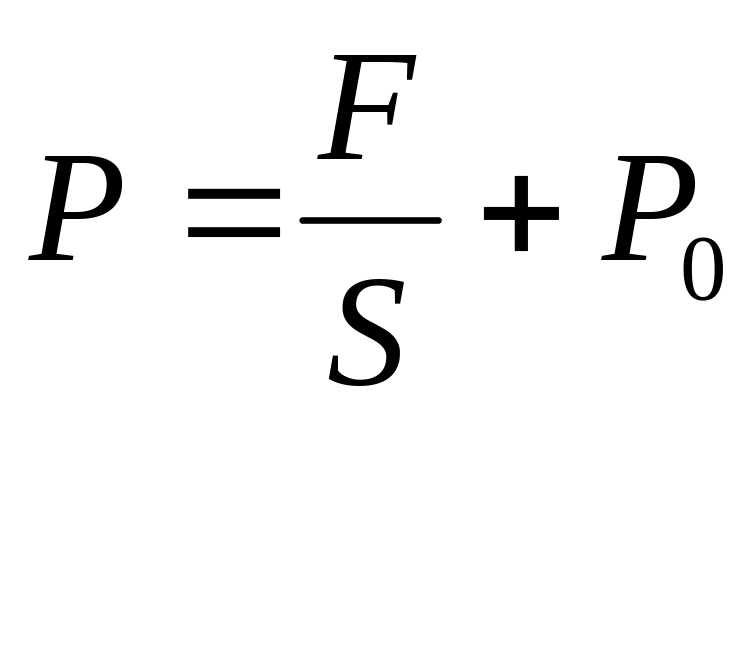
При нагревании объем не изменяется. По закону Шарля:

откуда:

Следовательно: = 420К.

2.13. В баллоне емкостью 110 л помещено 0,8 кг водорода, и 1,6 г кислорода. Определить давление смеси на стенки сосуда, если температура окружающей среды 27⁰С.

Решение.

Согласно закону Дальтона, давление смеси равно сумме парциальных давлений: Р=Р₁ +Р₂.

Здесь:

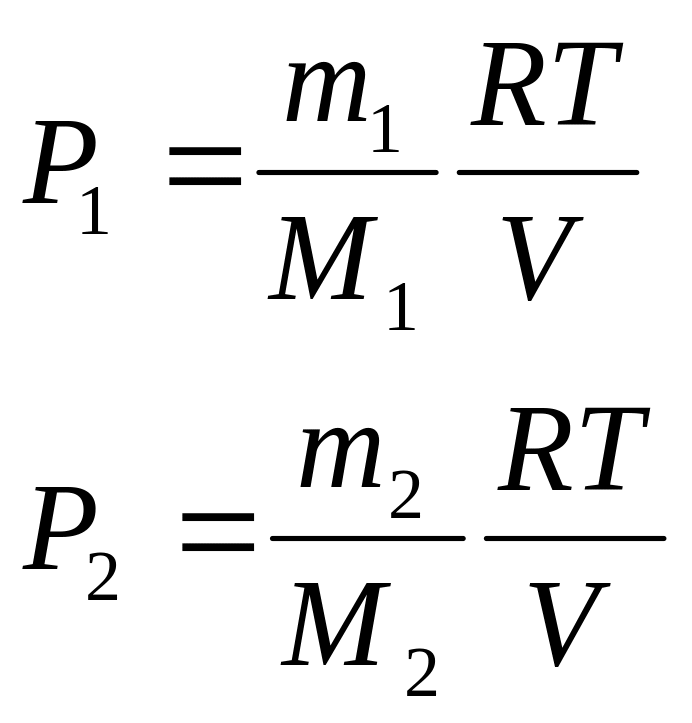
Тогда имеем: .

2.14. Сколько молекул ртути содержится в 1 см³ воздуха в помещении, зараженном ртутью, при температуре 20° С, если давление пара ртути при этой температуре равно 0,645 Па? Число Авогадро N_A = 6,023■ 10²³ молек/г-моль.

Решение.

Из условия задачи вытекает, что давление и температура воздуха близки к нор­мальным, т. е. в этом случае воздух с хорошим приближением можно рассматривать как смесь идеальных газов, для которых справедлив закон Дальтона.

Пусть в объеме V содержится N молекул рту­ти, имеющих суммарную массу m. Тогда

и, следовательно, число молекул ртути в единице объема

.

2.15. Определить давление и молекулярный вес смеси газов, состоящей из 10 г кислорода и 10 г азота, которые занимают объем 20 л при температуре 150° С.

Решение.

По закону Дальтона .

Придав правой части вид, совпадающий с урав­нением состояния идеального газа,

где по смыслу , находим для молекуляр­ного веса смеси

.

2.16. Пространство между двумя достаточно длинными цилиндрами с радиусами R₁ и R₂ заполнено идеальным газом, коэффициент теплопроводности которого равен . Тмепература внешнего цилиндра Т₂ , внутреннего – Т₁ (Т₁ > Т₂). Считая, конвекция газа отсутствует, а длина свободного пробега молекул газ меньше расстояния между цилиндрами, найти тепловой поток q_l, приходящийся на единицу длины цилиндров.

Решение.

Температуры внешнего и внутреннего цилиндров постоянны, поэтому в пространстве между ними устанавливается постоянное распределение температур Т(г), где г — расстояние до оси цилиндров. Поток тепла не будет зависеть от времени, т. е. процесс стационарный.

Выделим мысленно цилиндр радиусом, коаксиальный с данными цилиндрами, все точки которого имеют одинаковую температуру Т (r).Тепловой поток, проходящий через этот цилиндр,

,

где — коэффициент теплопроводности; S = — площадь поверхности цилиндра длиной / и радиусом г .

Необходимым условием стационарности процесса является независимость потока теплоты от радиуса цилиндра, т. е. q=const. Учитывая это, разделим переменные и проинтегрируем уравнение (1). Получим: .

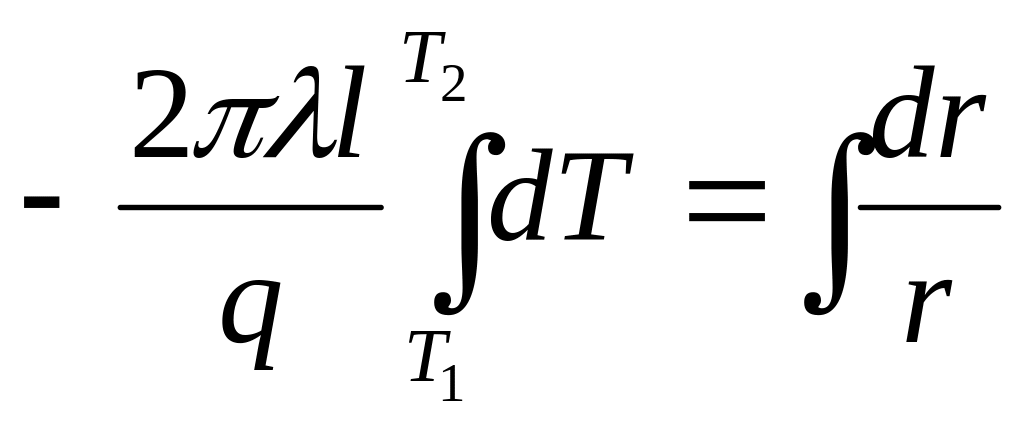откуда .