Введение в теорию идеального газа

1. Какую максимальную концентрацию мо­лекул углекислого газа, газокинетический диаметр которых равен d=3,2• 10^-10 м, можно образовать в сферическом сосуде диаметра D=1 м, чтобы средний свободный пробег превосходил величину диаметра? Решение.

2. Из основной формулы имеем п₀ < 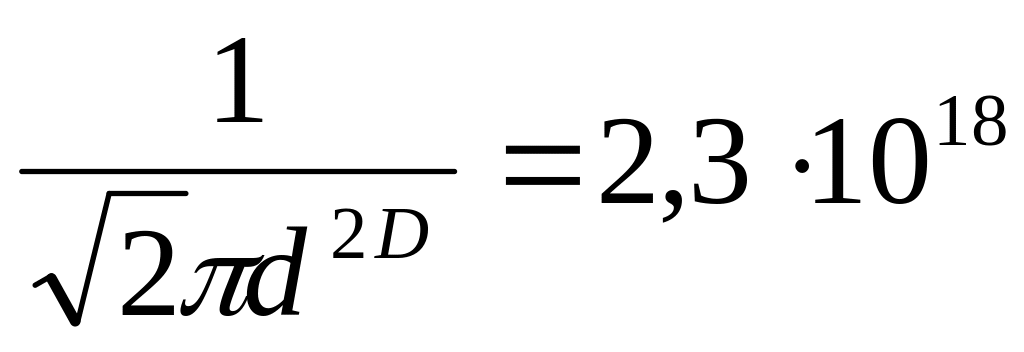м^-3.

2.2. Сколько молекул кислорода находится в объеме 1 л при температуре

0° С и давлении 133,3 Па?

Решение.

При решении используется основ­ная формула кинетической теории р = п₀кТ, (1)

где п₀ — число молекул в единице объема.

По­скольку 1 м³=10³ л, то искомое число молекул N связано с п₀ соотношением = п₀.

Следова­тельно, из (1) следует, что

N = ~ 3,5-10¹⁹,

где величины р, к, Т необходимо выразить в си­стеме СИ.

2.3. Каково давление в смеси газов емкостью 2 л, если в ней находится 10¹⁵ молекул кислорода и 10^-7 г азота, а температура смеси 50° С?

Решение.

По закону Дальтона

р = [п₀(О.₂)+п₀(N₂)]кТ, (1)

причем n₀(0₂) = 10¹⁵-0,5-10³ = 0,5-10¹⁸ м-³, а

п₀(N₂) = 0,5-10³ ( )N₀~ 1,1 • 10^-2 м³,

где учтено, что число Авогадро N₀ = 6-10²³.

Отсюда следует, что

Р = (n₀ (О_а) + n₀ (N₂)) kT = 0,72 • 10² Па.

2.4. Давление газа равно 10⁴ Па, а средняя квадратичная скорость равна 500 м/с. Найти плотность этого газа.

Решение.

Основное уравнение кинетической теории может быть представлено следующим об­разом: р =n₀кТ= — .

Следовательно,

= Зр/<V²> =0,12 кг/м³.

2.5. Чему равна энергия вращательного дви­жения двухатомного газа, находящегося под дав­лением р=10⁵ Па в сосуде объемом 1 л? Счи­тать, что вращательные степени свободы полно­стью возбуждены.

Решение.

Из основного кинетического урав­нения для плотности кинетической энергии Е мо­лекул имеем

Эта плотность энергии получается за счет трех поступательных степеней свободы каждой из мо­лекул. Вращательных степеней свободы две. Сле­довательно, плотность вращательной энергии рав­на

Е_вр = 2Е/3 = р.

Отсюда энергия вращательного движения в одном литре

Е_вр = =10 Дж.

2.6. На упругой нити с модулем кручения D=^10-15 Н-м подвешено зеркальце. Вследствие беспорядочных ударов молекул оно совершает ко­лебания. Определить средний квадрат амплитуды этих колебаний. Температура воздуха 20° С.

Решение.

Уравнение движения нити есть

где / — момент инерции зеркальца относительно оси кручения.

Отсюда следует закон сохранения энергии

¹/₂ + ¹/₂ D ² = сопst.

Следовательно, имеем

.

где использована теорема о равнораспределении энергии по степеням свободы.

Следовательно, .

Статистические закономерности

2.7. Выразить поток молекул N, падающих стенку сосуда, через плотность молекул п₀ и среднюю скорость <V>. Функцию распределения

f(V) по скорости считать изотропной.

Решение.

Условие нормировки функции распределения имеет вид:

где — элемент телесного угла.

По определению средней скорости имеем

<V>=

C другой стороны, отсчитывая углы 0 от нормали стенке, получаем

2.8. Определить отношение числа частиц N₁энергия которых меньше, чем Е₁ к числу частиц N₂, энергия которых больше этой величины.

Решение.

Используем распределение Максвелла, которое с учетом того, что может быть записано в виде

dN= А ехр (— Е/кТ) dE,

А — нормировочная постоянная.

Отсюда получаем:

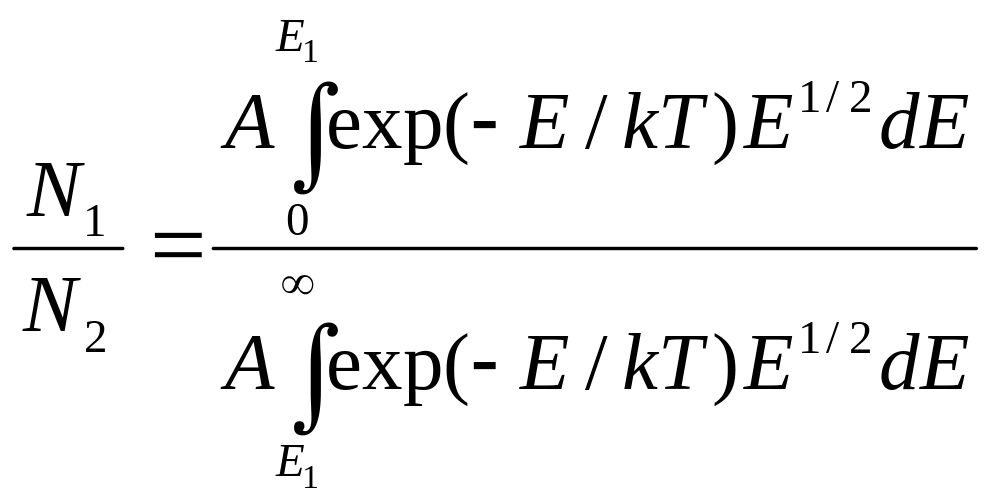
Эти интегралы подстановкой у = t² и интегрирова­нием по частям легко сводятся к табулированным интегралам ошибок.

2.9. Идеальный газ, имеющий температуру Т, вращается вместе с цилиндром высоты l и ра­диуса R вокруг своей оси с угловой скоростью . Найти давление газа на боковую стенку цилинд­ра, если общее число молекул в цилиндре N₀.

Решение.

В системе координат, связанной с вращающимся цилиндром, на молекулы идеально­го газа действуют силы инерции т ²г, направлен­ные от оси вращения. Следовательно, можно счи­тать, что газ находится в эффективном потенци­альном поле (—^]/2 ²г²) и поэтому распределение Больцмана имеет вид

dN = А ехр ( ² г²/2кТ) 2 dгdz, (1)

где А есть нормировочная постоянная, которая находится из условия

где N₀ — общее число частиц в цилиндре, V— объем цилиндра.

Имеем:

Отсюда для плотности распределения частиц по радиусу цилиндра получаем формулу

где учтено, что объем цилиндра . Давление на боковую стенку:

P(R) =n₀(R)kT.

2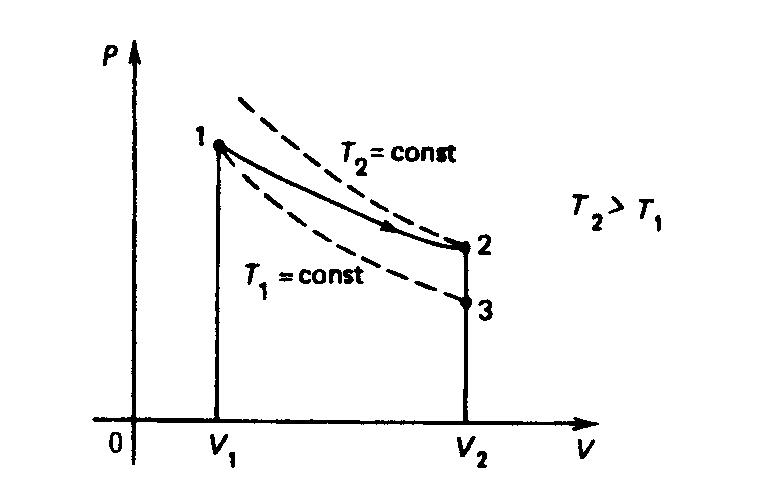 .10. Нагревается или охлаждается газ при переходе из состояния 1 в состояние 2? m=const.

Решение.

Изобразим на диаграмме P – V графики зависимости P(V) при изотермическом расширении газа. Изотерма, проходящая через точку 2, определяющую состояние 2, выше изотермы, проходящей через точку 1, определяющую состояние 1, следовательно, Т₂ > Т₁. Газ нагревается.

2.11. Нагревается или охлаждается газ, если процесс его расширения происходит по закону PVⁿ=const? Масса газа постоянна. Рассмотреть два случая: 1) n<1, 2) n>1.