Лабораторная работа № 3 бинарные деревья поиска
Цель работы: изучить структуру данных бинарных деревьев поиска, разработать класс TFindTree для работы с ней и получить практический навык его использования.
Теоретические сведения
Бинарное дерево поиска (FindTree) – это дерево, значение каждого узла которого удовлетворяют условию: левый сын меньше родительского узла, а правый сын - больше или равен родительскому узлу.
Рис. 1. Структура
бинарного дерева поиска
Таким образом, в левой ветви любого узла будут находиться узлы с меньшими значениями, а в правом – с большими или равными значениями, чем в самом узле.
Такая структура
данных позволяет сократить временные
затраты на поиск заданного значения
узла. В наилучшем случае искомый элемент
будет найден первым в корне дерева, а в
наихудшем случае – на последнем уровне.
Для этого потребуется k+1 сравнение,
где k – последний уровень дерева. В
среднем для поиска случайного элемента
потребуется 
сравнений.
Уровень дерева связан с количеством узлов n по формуле:
.
Поэтому, средние затраты на поиск будут определяться выражением:
.
Чем больше элементов в списке, тем выгодней использование бинарных деревьев поиска.
Например, при n
= 7 методом перебора потребуется в среднем
сравнения, а с помощью бинарных деревьев
сравнения.
При n
= 1023 методом перебора потребуется в
среднем 
сравнений, а с помощью бинарных деревьев
сравнений.
Рис.
2. Эффективность методов поиска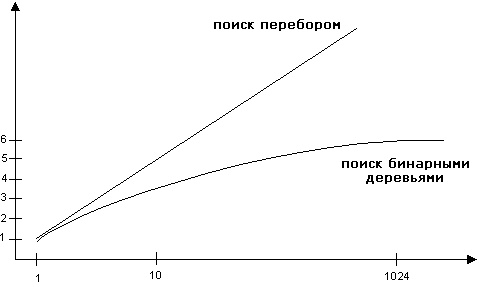 
Бинарное дерево поиска позволяет быстро отсортировать массив. Точнее, в бинарном дереве поиска, массив уже отсортирован по возрастанию или по убыванию. Для его получения достаточно провести симметричный проход дерева. Например, для дерева, представленного на рисунке 1, проход в порядке LNR даст отсортированный массив по возрастанию: (10, 20, 30, 40, 50, 60, 70), а в порядке RNL – по убыванию: (70, 60, 50, 40, 30, 20, 10).
Однако для бинарных деревьев поиска необходимо определенным образом добавлять и удалять узлы.
При вставке узла в бинарное дерево поиска может быть нарушена его структура, поэтому перед вставкой, необходимо найти позицию, куда необходимо вставить узел с новым значением.
Алгоритм вставки начинается с корня дерева. Если он существует, то осуществляется поиск места для вставки, если не существует, то вставляемый узел становится корнем. Поиск места осуществляется по правилу: если вставляемый узел меньше значения текущего узла, то место для вставки будет левым сыном, в противном случае – правым сыном. Поиск для вставки осуществляется до тех пор, пока не будет найден листовой узел. Текущий узел становится левым сыном найденного листа, если его значение меньше значения найденного узла и правым – наоборот.
Рис. 3. Вставленный узел становится левым сыном листа
Рис. 4. Вставленный узел становится правым сыном листа
При удалении узла могут возникнуть четыре случая:
1. Удаляемый узел является листом.
В данном случае необходимо из памяти удалить узел, первоначально разорвав его связь с родителем, установив ее в NULL.
Рис. 5. Удаление листового узла
Р
ис.
6. Дерево после удаление листового узла
2. Удаляемый узел имеет левого сына.
В данном случае необходимо первоначально разорвать связь с родительским узлом и сделать соответствующим наследником родителя левого сына удаляемого узла, который становится узлом замещения.
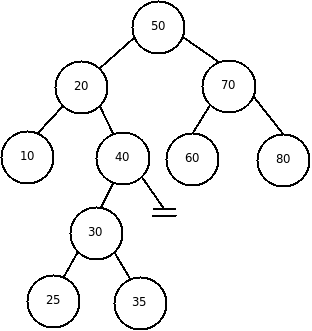
Рис. 7. Дерево перед удалением узла с левым поддеревом
Рис. 8. Дерево после удалением узла с левым поддеревом
3. Удаляемый узел имеет только правого сына
В данном случае узлом замещения становится правый сын, который становиться соответствующим сыном родителя удаляемого узла.
4. Удаляемый узел имеет и левого и правого сыновей.
Рис. 8. Дерево перед удалением узла
В данном случае возникает проблема нахождения замещающего узла. Ни левый, ни правый сын не могут стать ими, так как при этом может нарушиться структура бинарного дерева поиска.
Замещающий узел ищут либо в левой ветви удаляемого узла, используя принцип max-min, либо в правой ветви, используя принцип min-max.
По принципу max-min ищется максимальный элемент из минимальных элементов, находящихся в левом поддереве. Например, при удалении узла со значением 20, это узел 15.
По принципу min-max ищется минимальный элемент из максимальных элементов, находящихся в правой ветви. Например, при удалении узла со значением 20, это узел 30.
После нахождения максимального элемента из минимальных элементов, возникают две ситуации:
Замещающий узел является листом.
Рис. 9. Дерево перед удалением узла
В данном случае замещающий узел располагают вместо удаляемого узла, переустанавливая связи с родительским узлом, а также с родителем и с левым и с правым наследниками удаляемого узла.
Рис. 10. Дерево после удаления узла
Замещающий узел имеет левое поддерево.
Рис. 11. Дерево перед удалением узла
В данном случае первоначально в правую ветвь родителя замещающего узла добавляют левую ветвь замещающего узла.
Рис. 12. Дерево после удаления узла
При выполнении операции удаления узла в любом случае, первоначально переустанавливаются все связи с родителем. Только после сам узел удаляется из памяти.
ADT – формат класса TFindTreeNode
ADT TFindTree
Поля
Указатель на родительский узел (FParent): Тип узла
Данные узла (FData): Заданный тип
Уровень узла (FLevel): Целый тип
Список дочерних узлов (Items): Динамический массив узлов vector
Счетчик узлов (FCount): Целый тип
Методы
Конструктор
Вход: Родительский узел и данных нового узла
Предусловие: Нет
Начальные значения: Нет
Процесс: Инициализация полей объекта
Добавление дочернего узла (AddChild)
Вход: Данные дочернего узла
Предусловие: Нет
Процесс: Создание нового узла и добавление его в конец списка узлов
Постусловие: Новый элемент добавлен в конец списка и счетчик узлов увеличен на единицу.
Выход: Указатель на созданный узел
Вставка дочернего узла в указанную позицию (InsetChild)
Вход: Родительский узел, порядковый номер в списке родителя и данные нового узла.
Предусловие: Порядковый номер узла меньше количества узлов и не меньше нуля.
Процесс: Создание нового узла и добавление его в указанную позицию списка дочерних узлов.
Постусловие: Новый элемент добавлен в указанную позицию списка, и счетчик узлов увеличен на единицу.
Выход: Указатель на созданный узел
Удаление дочернего узла (DeleteChild)
Вход: Индекс узла в списке родителя
Предусловие: Порядковый номер узла меньше количества узлов и не меньше нуля.
Процесс: Удаление узла из списка родителя и упорядочивание в нем оставшихся элементов.
Постусловие: Счетчик узлов и длина дочернего списка уменьшены на единицу.
Выход: Нет
Деструктор (Destroy)
Вход: Нет
Предусловие: Нет
Процесс: Удаление из памяти всех дочерних узлов из списка.
Конец ADT TTreeNode