Санкт-Петербургский Государственный
Политехнический Университет
Ф
акультет
Технической Кибернетики
Кафедра Информационных и Управляющих Систем
Лабораторная работа по «тау» №2 Тема: качество систем автоматического управления
Вар: 18.
Выполнил:
Матвеева Наталья
Группа :3084/1
2012
Цель работы:
Исследовать критерии оценки качества САР.
Задачи:
1.
Построить корневой годограф системы
(распределение положения корней системы
в зависимости от параметра PAR1 исходной
системы); параметры
системы для построения корневых
годографов даны в отдельном задании
преподавателя;
варьируя значение параметра PAR1
попытаться
обеспечить
заданное (
)
расположение корней характеристического
уравнения.
2.
Ввести общую дополнительную обратную
связь с первого выхода на первый вход
и обеспечить заданное (
)
расположение корней характеристического
уравнения, сохранив
неизменными порядок системы и свойство
физической реализуемости.
Если
введение общей дополнительной обратной
связи не приводит к желаемым свойствам
системы, стабилизировать
систему
(обеспечить
)
изменением локальных обратных связей.
Последующие пункты задания выполняются для стабилизированной системы.
3. Ввести, если необходимо, дополнительные связи, превращающие систему в следящую по первому входу и первому выходу, и определить типовые установившиеся ошибки в полученной следящей системе.
4. Построить систему максимального быстродействия без перерегулирования (варьируя параметры PAR1 и PAR2).
Сравнить оценку быстродействия, получаемую по переходной функции, с приближенной, основанной на значении степени устойчивости (т.е. на значении ближайшего к мнимой оси корня характеристического уравнения).
5. Построить отклик стабилизированной системы на заданные входные воздействия.
Задание.
Вид передаточных функций для звеньев(из результатов прошлой лабораторной работы):
(1*)
Изменился
только вид знаменателя в w2,
т.к
А передаточные функции всей цепи:
;
(2*)
;
I.Обеспечение заданного расположения корней
I.1) Построение корневого годографа.
Теоретическая основа
Корневой годограф - траектория, описываемая на комплексной плоскости полюсами передаточной функции динамической системы при изменении одного из её параметров.
Пусть передаточная функция
замкнутой системы
,(причём
порядок полинома числителя равен
,
порядок полинома знаменателя равен
,т.е.
для физически реализуемых
систем). Метод корневого годографа
связывает характеристики системы с
поведением нулей и полюсов её передаточной
функции, которые находятся из нулей и
полюсов разомкнутой системы при изменении
какого-либо параметра в ней (коэффициента
усиления или постоянных времени). Все
графики строят в общей системе координат
-
.
Корневые годографы позволяют оценивать чувствительность системы к изменению того или иного параметра и выбирать его значение, обеспечивающее наиболее подходящее размещение корней из допустимого.
Опыт.
В нашем опыте имеем замкнутую систему, проведем исследование варьируя параметр par1, а par2 приравняем 5, как в задании к первой лабораторной работе. Моделирование производим в Program CC.
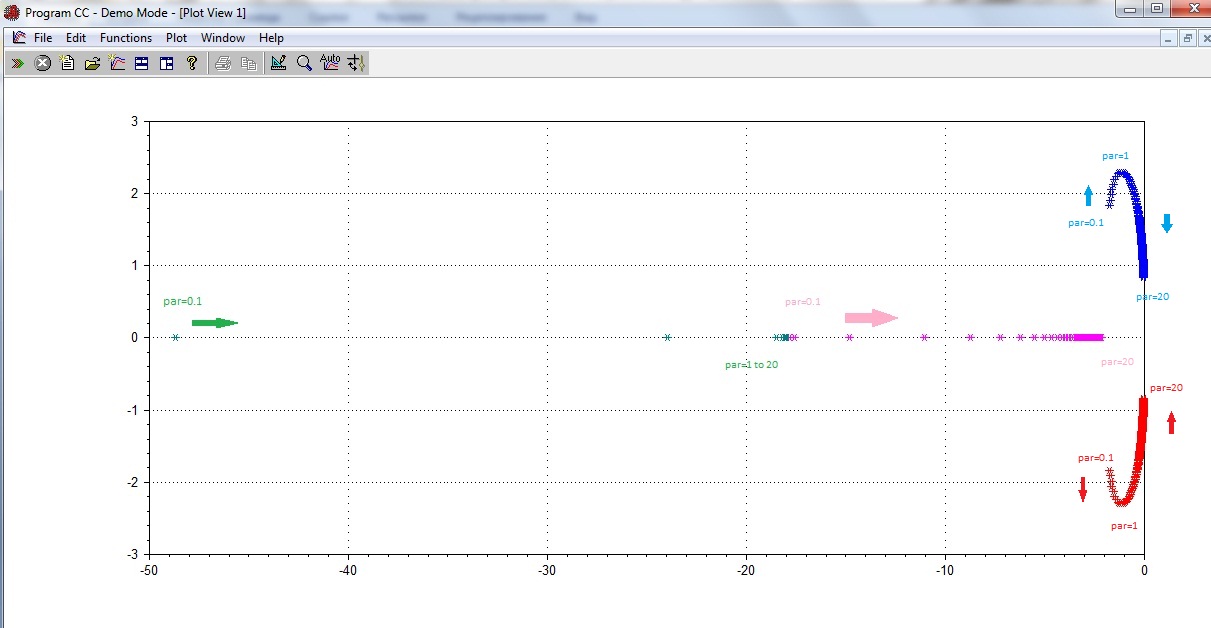
На рис. Представлен результат работы программы при изменении параметра от 0.1 до 20 с шагом 0.1. Нижняя граница выбрана из тех соображений, что при отрицательном значении параметра очевидно нарушится условие устойчивости системы, равенство его нулю приведет к потере степени. Рассмотрим более подробно годограф:
Данный рисунок изображает изменение par1 в диапазоне 0.1 – 1.0. Мы имеем два корня, лежащих на вещественной оси, и комплексно-сопряженную пару. Следует подчеркнуть свойства годографа:
Число ветвей корневого годографа равно порядку системы
.Симметричность относительно действительной оси комплексной плоскости.
Промоделируем при изменении параметра 1 в диапазоне 1.0-20 .Имеем:
Здесь видно, что при значениях par1
>1 один из корней обращается в const=-18
(зел.). Можно заметить, что при значениях
параметра>15 корни начинают слабо
отличаться друг от друга, поэтому
моделирование можно проводить более
короткое. Следует также отметить, что
сделав zoom графика, можно
посмотреть ,дошел ли график до im-оси
или нет.
На этом рисунке мы убеждаемся ,что ось не пересекаем. При моделировании системы с par1 порядка 10^3 , пришли к убеждению, что значение корня будет асимптотически стремиться к нулю.
Код программы:
par=1;
g=( (2/(s+18)) * (4/(par*s^2+5*s+7)) )/ ( 1+(2/(s+18)) * (4/(par*s^2+5*s+7)) + (4/(s+2))*(4/(par*s^2+5*s+7)) )
a=poles(g)
for par =0.1:0.1:20
aa= poles( g=( (2/(s+18)) * (4/(par*s^2+5*s+7)) )/ ( 1+(2/(s+18)) * (4/(par*s^2+5*s+7)) + (4/(s+2))*(4/(par*s^2+5*s+7)) ) )
a=[a aa]
end
plot(a(1,:),'*'); line(a(2,:),'*'); line(a(3,:),'*'); line(a(4,:),'*')
Исходному заданию ( ) соответствуют корни при всех рассмотренных нами параметрах. Единственное, когда мы можем добиться невыполнения задания, это при отрицательном параметре, что изначально иррационально.
В качестве примера выполнения приведем:
par1=0.2
H11(s) =40(s+2) / ( [(s+1,714)^2+1,911^2] (s+17,6)(s+23,97) ).