2. Решение двойственной задачи

2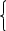 у1 + у2 ≥ 2,

у1 + 3у2 ≥ 3,

у1, у2 ≥ 0.

F(y1, y2) = 2у1 + 3у2 → min

1. Графический способ

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами. Обозначим границы области многоугольника решений ОАВС. Рассмотрим целевую функцию задачи F(y1, y2) = 2у1 + 3у2 → min.

Построим прямую, отвечающую значению функции F = 5: 2y1 + 3y2 = 5. Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике это прямая песочного цвета.

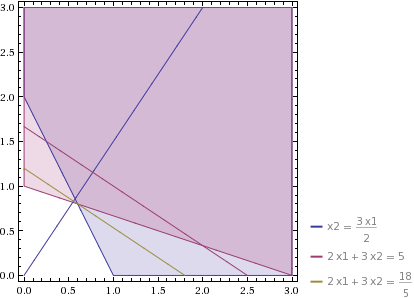
Пересечением полуплоскостей будет являться область, которая представляет собой многоугольник ОАВС, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Прямая F(y1, y2) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых 1 и 2, то ее координаты удовлетворяют уравнениям этих прямых:

2у1 + у2 = 2,

у1 + 3у2 = 3.

Решив систему уравнений, получим: у1 = 0.6, у2 = 0.8, откуда найдем минимальное значение целевой функции: Fmin = F(0.6, 0.8) = 2 * 0.6 + 3 * 0.8 = 3.6.

2. Поиск решения в ms Excel 2007

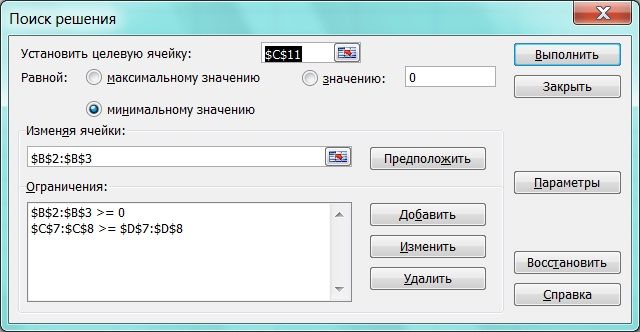
Значения х1 и х2 совпадают с графическим методом решения. Это наименьшая прибыль при производстве товара количеством Т1 = х1 = 0.6 и Т2 = х2 = 0.8.

3. Аналитический способ (симплекс-метод)

По условию задачи необходимо минимизировать целевую функцию. Тогда, основываясь на результатах проверки условия A, применим к данной целевой функции оператор M. Также все неравенства системы линейных ограничений содержат знаки «больше или равно». Тогда, основываясь на результатах проверки условия B, применим к каждому неравенству данной системы ограничений оператор N. Тогда в каноническом виде система примет следующий вид:

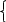- 2у1 – у2 – у3 = -2,

-у1 – 3у2 – у4 = -3.

F(y1, y2) = -2у1 – 3у2 → max

Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции.

		1	2	0	γ
	0	-2	-3	0	1
	3	-2	-1	-2
	4	-1	-3	-3

Первая итерация (k = 1). Вычислим текущее допустимое решение: у1 = у2 = 0, у3 = 2, у4 = 3, F = 0.

Так как преобразованная система линейных ограничений содержит отрицательные свободные члены (выполняется условие D), то к полученной на предыдущем этапе симплекс-таблице необходимо применить оператор K – поиск опорного решения.

В соответствии с алгоритмом поиска опорного решения возьмем любое неравенство системы ограничений, содержащее отрицательный свободный член, например первое неравенство (индекс строки в симплекс-таблице 3), и выберем в нем любой отрицательный элемент, например первый (он равен -2). Тогда в качестве e-столбца будет выступать столбец 1, т.е. е = 1. Для определения s-строки необходимо, прежде всего, рассчитать столбец . Результаты расчетов представлены ниже:

		e
		1	2	0	γ
	0	-2	-3	0	1
s	3	-2	-1	-2	-2 ÷ (-2) = 1 - min
	4	-1	-3	-3	-3 ÷ (-1) = 3

В соответствии с алгоритмом поиска опорного решения на данной итерации индекс s строки равен 2, т.е. s = 3.

В соответствии с алгоритмом симплекс-метода произведем замену e-столбца и s-строки. В результате получим следующую симплекс-таблицу:

		3	2	0	γ
	0	-1	-3 – 1/2 * (-2) = -2	0 – 1 * (-2) = 2	2
	1	-1/2	1/2	1
	4	-1/2	-3 – 1/2 * (-1) = -5/2	-3 – 1 * (-1) = -2

Вторая итерация (k = 2). Вычислим текущее допустимое решение: у3 = у2 = 0, у1 = 1, у4 = -2, F = 2.

Так как преобразованная система линейных ограничений содержит отрицательный свободный член (строка с индексом 4), т.е. выполняется условие D, то к полученной на предыдущем этапе симплекс-таблице необходимо снова применить оператор K – поиск опорного решения.

В соответствии с алгоритмом поиска опорного решения возьмем второе неравенство системы ограничений (индекс строки в симплекс-таблице 4), и выберем в нем любой отрицательный элемент, например второй (он равен -5/2). Тогда в качестве e-столбца будет выступать столбец 2, т.е. e = 2.

Для определения s-строки необходимо дополнительно рассчитать столбец . Результаты расчетов представлены ниже:

			е
		3	2	0	γ
	0	-1	-2	2	2
	1	-1/2	1/2	1	1 ÷ 1/2 = 2
s	4	-1/2	-5/2	-2	-2 ÷ (-5/2) = 4/5 - min

В соответствии с алгоритмом поиска опорного решения на данной итерации индекс s строки равен 3, т.е. s = 4.

В соответствии с алгоритмом симплекс-метода произведем замену e-столбца и s-строки. В результате получим следующую симплекс-таблицу:

		3	4	0	γ
	0	-1 – 1/5 * (-2) = -3/5	-4/5	2 – 4/5 * (-2) = 18/5	3
	1	-1/2 – 1/5 * 1/2 = -3/5	1/5	1 – 4/5 * 1/2 = 3/5
	2	1/5	-2/5	4/5

Третья итерация (k = 3). Вычислим текущее допустимое решение: у3 = у4 = 0, у1 = 3/5, у4 = 4/5, F = 18/5.

Так все коэффициенты при свободных переменных отрицательны, то найденное решение является единственным оптимальным решением данной задачи. Улучшить найденное решение не возможно.

Значит, Fmin = F(0.6, 0.8) = 3.6. Получили тот же ответ.