13. Связь между криволинейными интегралами первого и второго рода
Утверждения
7. Связь между криволинейными интегралами 1 и 2 рода
Пусть
- гладкая кривая, заданная уравнениями
,
и пусть
- вектор-функция, определенная и
ограниченная на этой кривой. Тогда
имеет место равенство
,
где
- угол между касательной к кривой
в точке
и положительным направлением оси
.
При этом стоящий слева интеграл
существует, если существует криволинейный
интеграл первого рода, стоящий в равенстве
справа.
14. Геометрический и физический смысл криволинейного интеграла первого и второго рода
Утверждения
4. Геометрический и механический смысл криволинейного интеграла первого рода
Геометрический смысл. Площадь
цилиндра, направленного по кривой
с образующей, параллельной оси
.
Механический смысл. Масса материальной
кривой
,
вдоль которой распределены массы с
плотностью
:
.
6. Физический смысл криволинейного интеграла второго рода
Криволинейный интеграл 2-го рода физически
представляет собой работу, совершаемую
силой
вдоль кривой
и равную
.
15. Вычисление криволинейного интеграла первого рода в случае параметрического задания кривой
Умения
2.1. Вычислить криволинейный интеграл 1-го рода в случае параметрического задания кривой:
,
где
- кривая
,
.
Решение:
Найдем дифференциал дуги кривой, заданной параметрически:
Получим интеграл:
Ответ:
.
16. Вычисление криволинейного интеграла первого рода в случае явного задания кривой
Умения
2.2. Вычислить криволинейный интеграл 1-го рода в случае явного задания кривой:
,
отрезок прямой
,
.
Решение:
Найдем дифференциал дуги кривой, она задана в явном виде:
.
Подставляем в интеграл
и
,
ставим пределы интегрирования:
Ответ:
.
17. Вычисление криволинейного интеграла первого рода в случае неявного задания кривой
Умения
2.3. Вычислить криволинейный интеграл 1-го рода в случае неявного задания кривой:
,
где С-окружность
.
Решение:
Перейдем к полярным координатам:
Подставим в наше уравнение окружности:
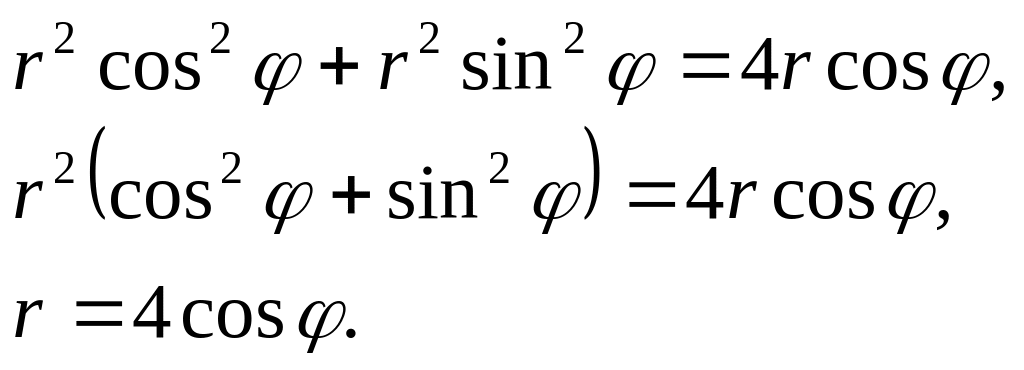
Дифференциал дуги кривой, в случае неявного задания, ищется по следующей формуле:
Исходный интеграл примет вид:
Ответ: 0.
18. Вычисление криволинейного интеграла второго рода в случае параметрического задания кривой
Умения
3.1. Вычисление криволинейного интеграла 2-го рода в случае параметрического задания кривой
Вычислить криволинейный интеграл 2-го рода в случае параметрического задания кривой.
где С – арка циклоиды
.
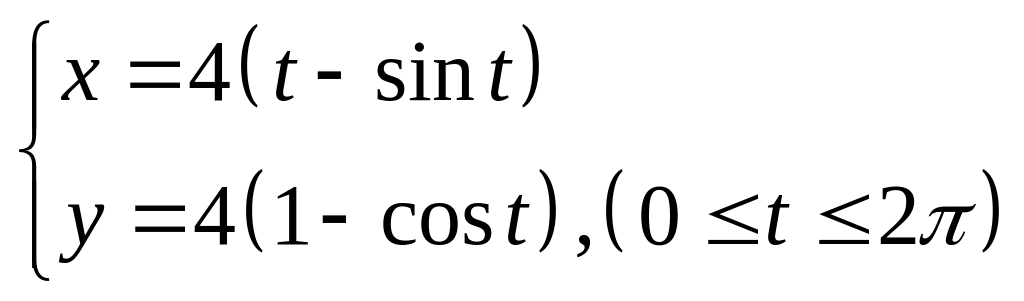Решение:
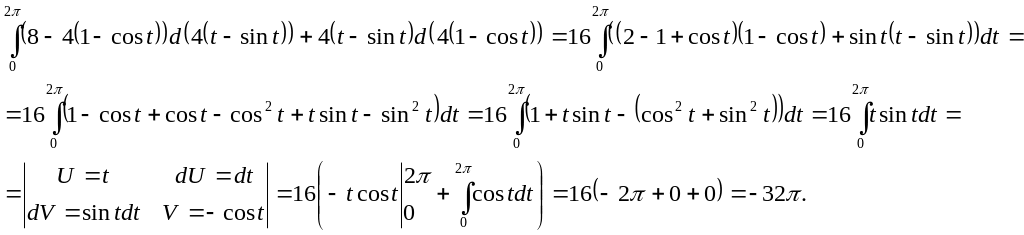Ответ:
.
Вычислить интеграл
,
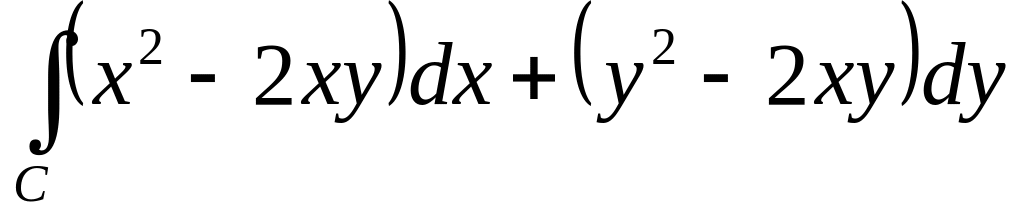где
.
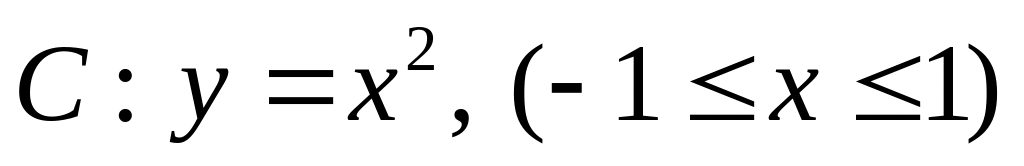Решение.
Выразим все через t:
Получаем, что наш интеграл равен
Ответ:
.
19. Вычисление криволинейного интеграла второго рода по кривой, заданной в полярных координатах
Умения
3.2. Вычислить криволинейный интеграл 2-го рода по кривой, заданной в полярных координатах.
,
- часть дуги
,
Решение:
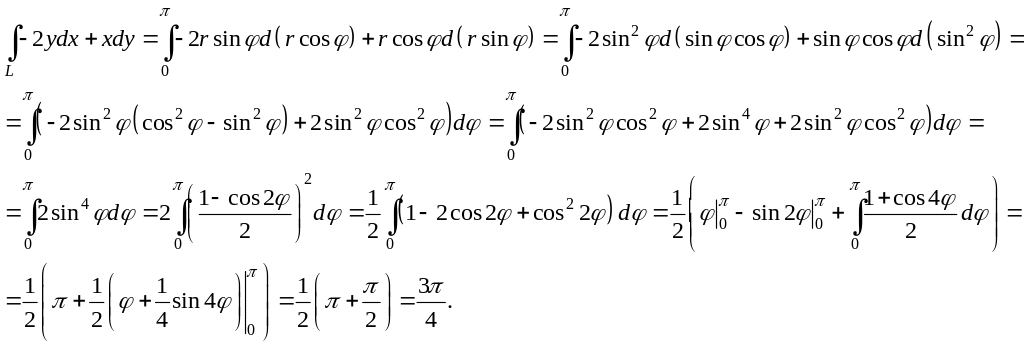Ответ:
.
20. Связь криволинейного интеграла второго рода по замкнутому контуру с двойным интегралом по области, ограниченной этим контуром
Утверждения