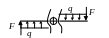2.1 Порядок выполнения расчета при растяжении и сжатии

2.1.1 Начертить схемы нагружения стержней (рисунки 2.1 – 2.3) и нанести на схемы численные значения размеров участков и нагрузок.

2.1.2 Вычислить реакции опоры (Н_А). От продольных внешних сил (нагрузок) в заделке возникает только одна продольная реакция Н_А. Для ее вычисления составляется одно уравнение равновесия статики. Сумма всех внешних сил и реактивной силы (Н_А) должна быть равна нулю – Σ F_i(Z) = 0. Из этого уравнения определяется реакция Н_А.

2.1.3 Вычислить ВСФ (N_Z) и построить эпюру N_Z.

При вычислении ВСФ применяется метод сечений. Суть метода:

- элемент конструкции или деталь машины (стержень, вал, балка, стойка, ригель), в данном случае стержень, находится в равновесии;

- в том месте по длине стержня, которое нас интересует, мысленно делается разрез;

- одна часть отбрасывается (обычно та, к которой приложено больше нагрузок);

- составляется уравнение равновесия статики для оставшейся части стержня с ее нагрузками: N_Z = Σ F_i^внеш.(Z) – внутренняя продольная сила N_Z равна сумме проекций на продольную ось Z всех внешних сил, действующих на оставшуюся часть стержня.

При этом надо соблюдать правило знаков N_Z (см. таблицу 2.2). После этого строится по участкам эпюра N_Z (эпюра – график, изображающий изменение ВСФ вдоль стержня, вала, балки и т.д.). Положительные значения откладываются вверх от нулевой линии, а отрицательные значения - вниз.

2.2 Порядок выполнения расчета при кручении

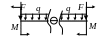
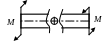
2.2.1 Начертить схему нагружения вала (рисунок 2.4) и нанести на схему численные значения размеров участков и крутящих моментов.

2.2.2 Вычислить реактивный крутящий момент в заделке (в защемлении).

От внешних крутящих моментов в заделке возникает только один реактивный крутящий момент М_R. Для его вычисления составляется только одно уравнение равновесия статики: сумма всех внешних крутящих моментов и реактивного момента в заделке должна быть равна нулю – Σ М_i(Z) = 0. Из этого уравнения определяется реактивный момент М_R.

2.2.3 Вычислить внутренние крутящие моменты М_Z и построить эпюру М_Z.

При вычислении М_Z также применяется метод сечений. Составляется уравнение равновесия для оставшейся части вала: М_Z = Σ М_i^внеш.(Z) – внутренний крутящий момент М_Z равен сумме моментов относительно оси Z всех внешних крутящих моментов, действующих на оставшуюся часть вала.

При этом надо соблюдать правило знаков М_Z (см. таблицу 2.2). После этого строится по участкам эпюра М_Z. Положительные значения откладываются вверх от нулевой линии, а отрицательные значения - вниз.

2.3 Порядок выполнения расчета при изгибе балки и рамы

2.3.1 Начертить схему нагружения балки или рамы (рисунки 2.5 – 2.8) и нанести на схему численные значения размеров участков, изгибающих моментов, сил – сосредоточенных и распределенных при их наличии.

2.3.2 Вычислить реакции опор.

Для заданной балки или рамы с шарнирными опорами, в опорах указывается предварительное направление опорных реакций. Составляются два уравнения равновесия статики: Σ М_i(А) = 0 и Σ М_i(В) = 0. Из них определяются две реакции опор – R_A и R_B (А и В – шарнирные опоры балки или рамы), направленные параллельно оси У. Если найденные значения опорных реакций получились со знаком «минус», это указывает на то, что предварительное направление опорных реакций указано неправильно и надо его поменять на противоположное, а значение на схеме указать без знака. В раме в шарнирно-неподвижной опоре возникает еще одна опорная реакция Н направленная параллельно оси Х, которая определяется из уравнения: Σ F_i^внеш.(Х) = 0.

После этого надо выполнить проверку правильности вычисления значений и направлений реакций опор с помощью следующего уравнения равновесия: Σ F_i^внеш.(У) = 0, то есть сумма проекций всех внешних и реактивных сил на вертикальную ось У должна быть равна нулю.

Для балок и рам с заделкой в сечении «А» (защемлением) с одной стороны, также составляются два уравнения равновесия: 1) Σ F_i^внеш.(У) = 0, и 2) Σ М_i(А) = 0. Из первого уравнения вычисляется вертикальная реакция в заделке R_A, а из второго уравнения – реактивный момент М_А. Для рамы дополнительно составляется уравнение Σ F_i^внеш.(Х) = 0, из которого определяется еще одна опорная реакция Н_А.

Для проверки решения составляется уравнение равновесия в виде суммы моментов всех сил относительно любого другого сечения «С» балки или рамы (Σ М_i(С) = 0).

2.3.3 Вычислить ВСФ при изгибе балки или рамы.

При вычислении ВСФ применяется метод сечений. В балках составляются два уравнения:

1) Q_у = Σ F_i^внеш.(У) – поперечная (внутренняя) сила Q_у равна сумме проекций на вертикальную ось У всех внешних сил, действующих на оставшуюся часть балки;

2) М_х = Σ М_i(Х) – изгибающий (внутренний) момент М_х равен сумме моментов относительно оси Х, всех внешних сил, действующих на оставшуюся часть балки.

При этом надо соблюдать правило знаков Q_у и М_х (см. таблицу 2.2).

После этого строится по участкам эпюра Q_у. Положительные значения откладываются вверх от нулевой линии, а отрицательные значения - вниз.

Положительные значения М_х откладываются на растянутой (выпуклой) стороне балки, то есть надо положительные значения М_х откладывать вниз от нулевой линии, а отрицательные значения М_х – вверх от нулевой линии.

Для рамы вычисляются и строятся эпюры трех ВСФ: N_z, Q_y, M_x.

Таблица 2.2 – Правило знаков ВСФ

ВСФ		+ (плюс)		- (минус)
Название	Обозна-чение	Направление обхода
		Слева	Справа	Слева	Справа
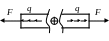
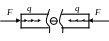
Продольная сила	Nz
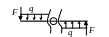
Поперечная сила	Qy
Изгибающий момент	Mx
Крутящий момент	Mz