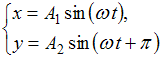Тема: Сложение гармонических колебаний Общий вид колебаний вдоль одного направления

1. Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами . Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания. 1.   2. 3.   0

1
2
3
			0

Решение: Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле ,  где и  – амплитуды, ( ) – разность фаз складываемых колебаний. Если разность фаз , , то  и . Если , , то . Если , , то .

2. Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными  и . Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний. 1. 2. 3.

1
2
3

Решение: Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле , где и  – амплитуды складываемых колебаний, ( ) – разность их фаз. Если амплитуда результирующего колебания , то . Тогда  и разность фаз складываемых колебаний равна . Если , то . Тогда , следовательно, . Если , то . Тогда , следовательно, .

3. Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными  и . Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания. 1. 0 2. 3.

1
2
3

Решение: Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле , где и  – амплитуды, ( ) – разность фаз складываемых колебаний. Если разность фаз , , то  и . Этот результат можно было получить сразу: при разности фаз  векторы  и  сонаправлены, и длина результирующего вектора  равна сумме длин складываемых векторов. Если   , то  и . Если   , то  и .

Общий вид колебаний вдоль двух взаимноперпендикулярных направлений

1. Складываются два взаимно перпендикулярных колебания. Установите соответствие между номером соответствующей траектории и законами колебаний точки вдоль осей координат  

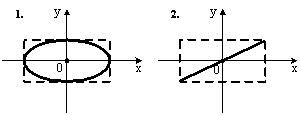
1
2
3
4

Решение: При одинаковой частоте складываемых колебаний уравнение траектории точки имеет вид: 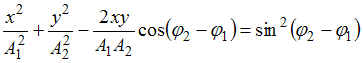, где  – разность фаз колебаний. Если разность фаз , то уравнение преобразуется к виду 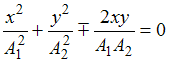, или 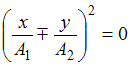, что соответствует уравнению прямой: . Если , то 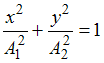, что является уравнением эллипса, причем если амплитуды равны , то это будет уравнение окружности. Если складываются колебания с циклическими частотами  и , где и целые числа, точка описывает более сложную кривую, которую называют фигурой Лиссажу. Форма кривой Лиссажу зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний.

2. Складываются взаимно перпендикулярные колебания. Установите соответствие между формой траектории и законами колебания точки вдоль осей координат   1. Прямая линия 2. Окружность 3. Фигура Лиссажу

1
2
3

Решение:

Для анализа формы траектории оба уравнения должны быть выражены относительно одной гармонической функции ( sin и sin или cos и cos).

Если частоты одинаковы и разность фаз 0, ±π, … – прямая линия

Если частоты одинаковы и разность фаз ±1/2π, ±3/2π,… – эллипс.(одинаковые амплитуды-окружность)

Если частоты кратны друг другу – фигуры Лиссажу

3. Складываются взаимно перпендикулярные колебания. Установите соответствие между законами колебания точки вдоль осей координат   и формой ее траектории. 1. 2. 3.

1			прямая линия
2			эллипс
3			фигура Лиссажу
			cинусоида

Решение:

Для анализа формы траектории оба уравнения должны быть выражены относительно одной гармонической функции ( sin и sin или cos и cos).

Если частоты одинаковы и разность фаз 0, ±π, … – прямая линия

Если частоты одинаковы и разность фаз ±1/2π, ±3/2π,… – эллипс.(одинаковые амплитуды-окружность)

Если частоты кратны друг другу – фигуры Лиссажу.