Типовой расчет 5, Вариант 8

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” имени В.И. Ульянова (Ленина)»

(СПбГЭТУ)

Кафедра высшей математики

Типовой расчет № 1.4

Вариант 8

Выполнил: студент группы 7811 (А.В. Петровский)

Проверил: (К.Ф. Мус) 

Санкт-Петербург

2007

Задание

а) Найти собственные числа и векторы матриц

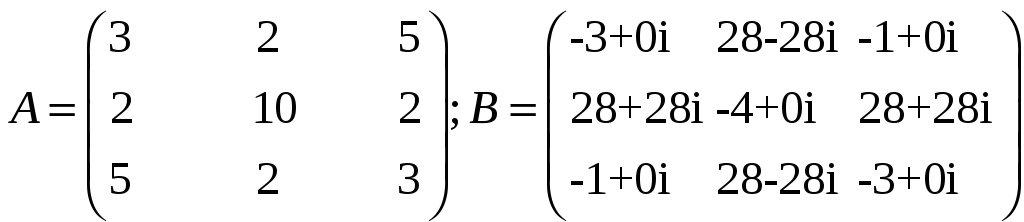
б) Привести уравнение кривой второго порядка к каноническому виду и изобразить ее на координатной плоскости

Определения, обозначения, соотношения, используемые в работе

Собственные числа и векторы матрицы.

Пусть A_m - квадратная матрица и XR^m _-- "m" - мерный вектор. Для них определено произведение Y=A_mX, причем YR^m. Таким образом, матрица «отображает» вектор в новый вектор:

Например,

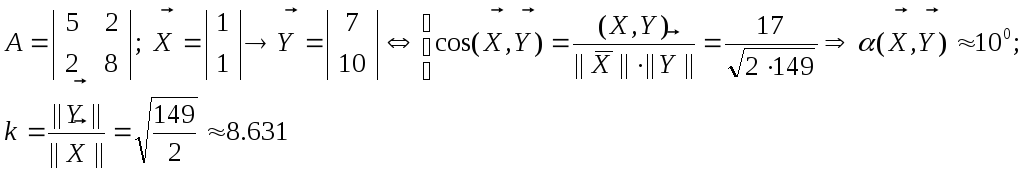
В общем случае этому отображению соответствуют два геометрических преобразования:

1. "поворот" на угол α=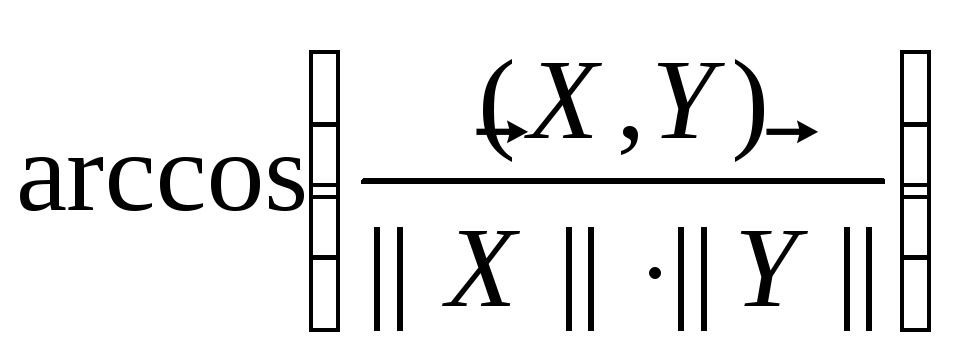 и (2) "растяжение" с коэффициентом k=||Y||/||X||.

Однако, среди векторов XR^m есть "особенные векторы", которые отображаются матрицей в коллинеарные векторы: .

Определение. Комплексное число λС и ненулевой вектор X_λ0 называются собственными значениями матрицы (собственным числом и соответствующим ему собственным вектором матрицы), если они удовлетворяют уравнению

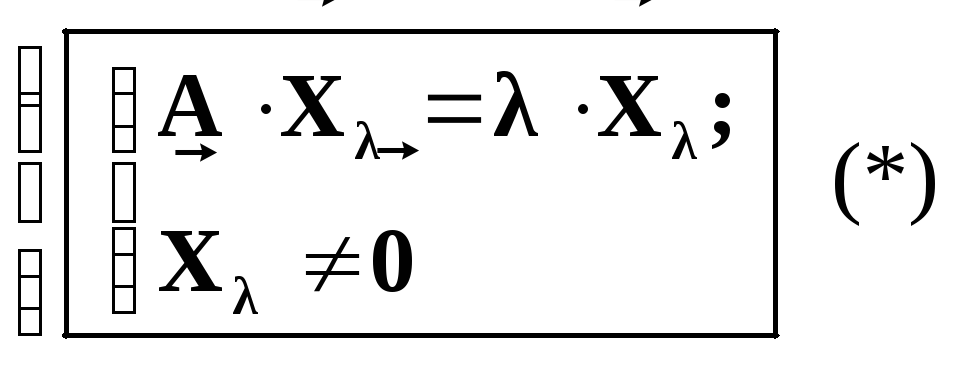
При решении уравнения (*) возникают три вопроса: (1) существует ли его решение – (;x_)?, (2) единственно ли оно? и (3) как найти все решения? Ответ на эти вопросы дает

Теорема. Квадратная матрица порядка "m" имеет ровно "m" собственных чисел: A_m {(_I;x_i); I=1m}.

Док-во.

Используя свойство единичной матрицы , запишем уравнение (*) в виде:

Таким образом, уравнение (*) равносильно однородной системе линейных алгебраических уравнений. Из теоремы Крамера известно, что однородная СЛАУ имеет ненулевые решения только при условии det(A-λI)=0. Определитель матрицы системы

является полиномом степени "m" относительно . По основной теореме алгебры этот полином имеет в C ровно "m" корней - "m" собственных чисел матрицы: P_m()=0(₁,₂,..,_m}.<= ч.т.д.

Например,

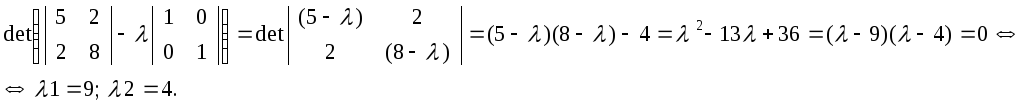
После того как найдены собственные числа матрицы, соответствующие собственные векторы находятся как ненулевые решения однородной СЛАУ

(A - λ _iI)X_i=0; i=1,2,..,m.

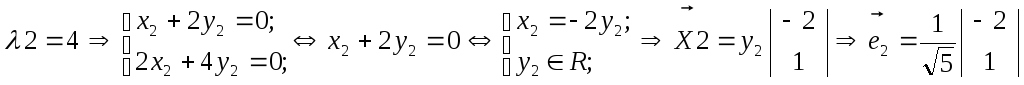
Таким образом, если каждое собственное число матрицы определяется однозначно как корни полинома, то соответствующие ему собственные векторы образуют множество коллинеарных векторов (определяются с точностью до произвольного множителя). Выберем из этого множества единичный вектор:

Отметим (без доказательства)

Свойства собственных значений (_I;x_i) симметричной матрицы A=[a_ik]; a_ik=a_ki; i,k=1,2,..,m.

1]Собственные числа симметричной матрицы вещественны - λ _i R; i=1:m.

2]Собственные векторы симметричной матрицы , соответствующие различным собственным числам, попарно ортогональны - λ _i#λ_k  (e_i,e_k)=0.

3] Если матрица имеет "m" различных собственных чисел (_i_j), соответствующие собственные векторы матрицы образуют ортогональный базис ЛВП R^m.

Геометрически это означает, что в R² (на плоскости) и в R³ (в трехмерном пространстве) собственные векторы матрицы определяют новую прямоугольную систему координат, которая получается поворотом "стандартной системы": XOY(i,j,k)X’OY’(e₁,e₂,e₃)

В рассмотренном примере: XOY(i,j)X’OY’(e₁,e₂) эта новая прямоугольная система координат на плоскости получена поворотом координатных осей "i,j" на угол α=arccos(i,e₁)= arccos(j,e₂)= arccos(1/)≈63.4⁰.

Приведение уравнения кривой второго порядка к каноническому виду.

В общем случае уравнение (*) Ax²+2Bxy+Cy²+Dx+Ey+F=0 определяет на в прямоугольной системе координат XOY(i,j) на плоскости точку (Ax²+By²=0), две прямые (Ax²-By²=0Ax+By=0; Ax-By=0) или кривые второго порядка: эллипс, гиперболу или параболу. Канонические уравнения этих кривых в прямоугольной системе координат , координатные оси которой совпадают с осями симметрии кривой, а начало координат находится в вершине параболы или в центре симметрии эллипса или гиперболы, имеют вид:

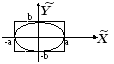
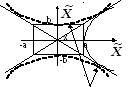
(1) (4)

Эллипс  с полуосями "а" и "в" гипербола парабола

Таким образом, геометрически приведение уравнения (*) к каноническому виду (1-4) предполагает выполнение двух последовательных преобразований системы координат : 1) преобразование "поворота" ,

и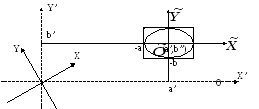 2) преобразование параллельного переноса системы координат в новое начало

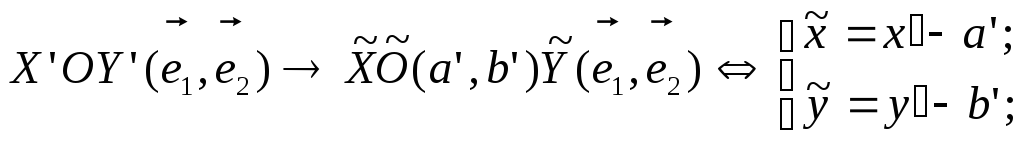
Прежде чем сформулировать алгоритм этих преобразований, заметим, что "квадратичная форма" Ф(х,y)=(Ax²+2Bxy+Cy²) уравнения (*) может быть записана как скалярное произведение

АЛГОРИТМ «приведения».

1) По "квадратичной форме" построим симметричную матрицу , и обозначим радиус-вектор точки М(х,у).

например, 5х²+4ху+8у²K=

2) Найдем собственные значения (₁,e₁); (₂,e₂) матрицы К:

1. собственные числа: det[K-I]=0{₁;₂}

2.2 единичные собственные векторы:

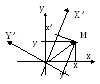
Если ₁₂, (e₁,e₂)=0 e₁e₂ новая прямоугольная

система координат: XOY(i,j)X’O Y’(e₁,e₂).

3) Разложим радиус-вектор точки плоскости по базису {e₁,e₂}

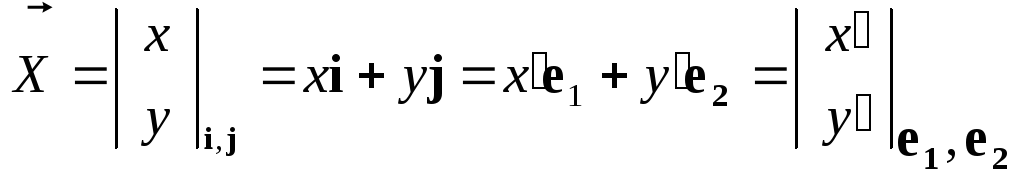
и запишем квадратичную форму в новой системе координат , учитывая, что

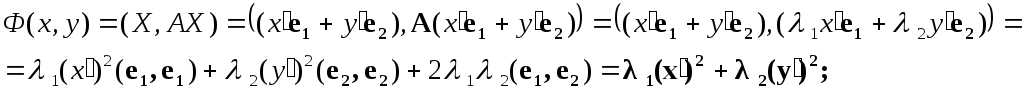
Таким образом, в новой системе координат X’OY’ квадратичная форма имеет канонический вид

-----------------------------------------

5x²+4xy+8y² 

4) Преобразуем к новой системе координат линейные слагаемые Dx+Ey:

;

---------------------------------------------------------------------



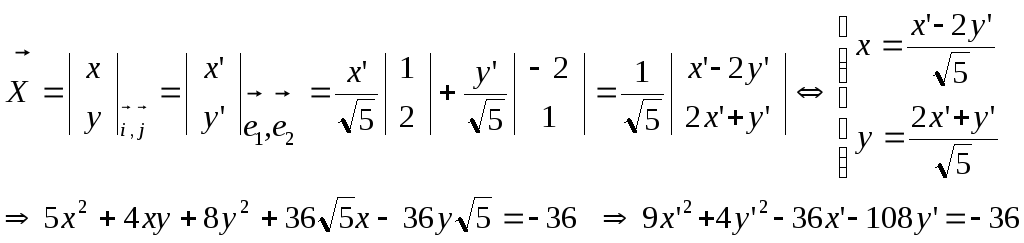
5) В слагаемых, соответствующих ненулевым собственным числам (_i0), выделим «полные квадраты»

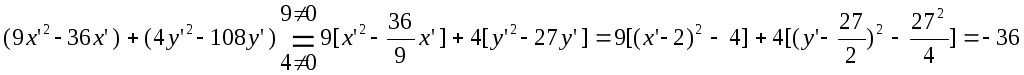
и введем новую систему координат (выполним преобразование параллельного переноса)- 

Таким образом, каноническое уравнение кривой имеет вид

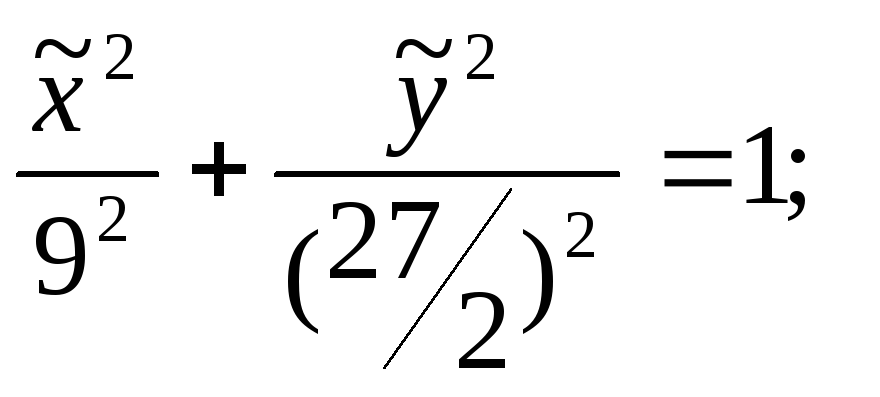
и определяет в пространстве эллипс с полуосями «9» и «13.5».

Замечания: уравнение (*) определяет

• параболу, если одно из собственных чисел матрицы К равно нулю (₁=0;₂0).

• Эллипс, если собственные числа матрицы одного знака (₁₂>0).

• Гиперболу, если матрица квадратичной формы имеет собственные числа «разного» знака (₁₂<0).

Вычиcление Det в п правилу Сариуса:

Det()=

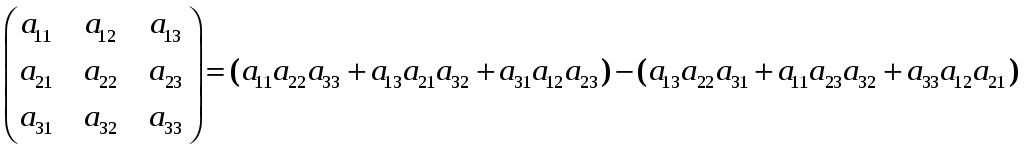
Выполнение работы

а)

Это диагональная матрица. Найдем собственные числа.

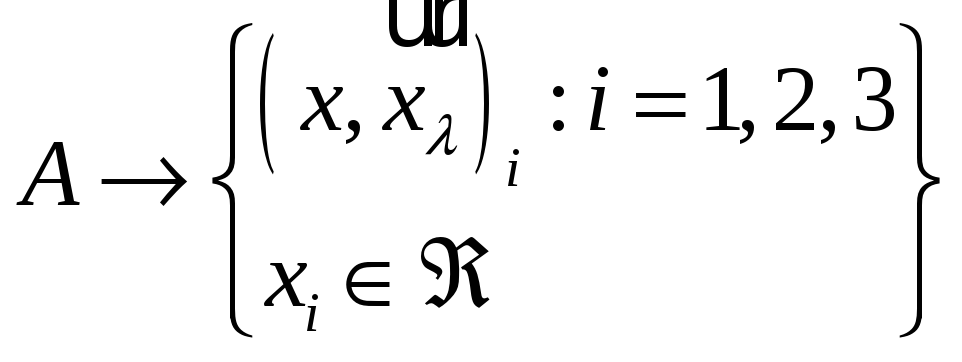
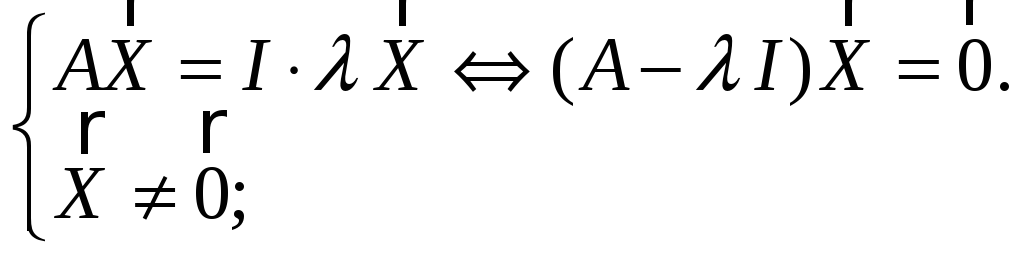
det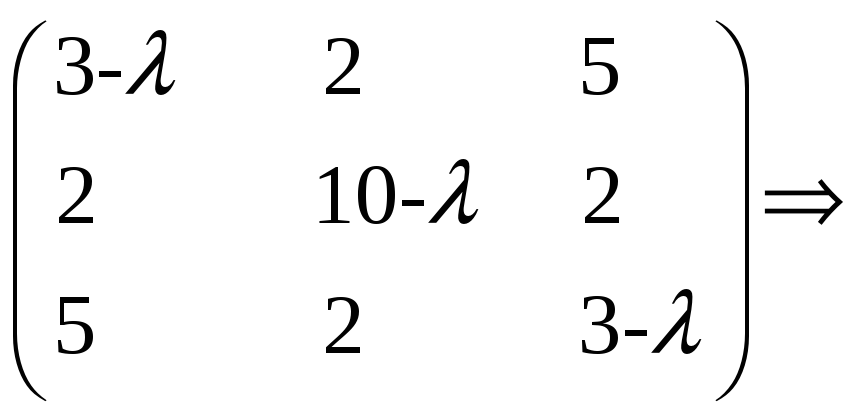по правилу Сариуса получим

вектор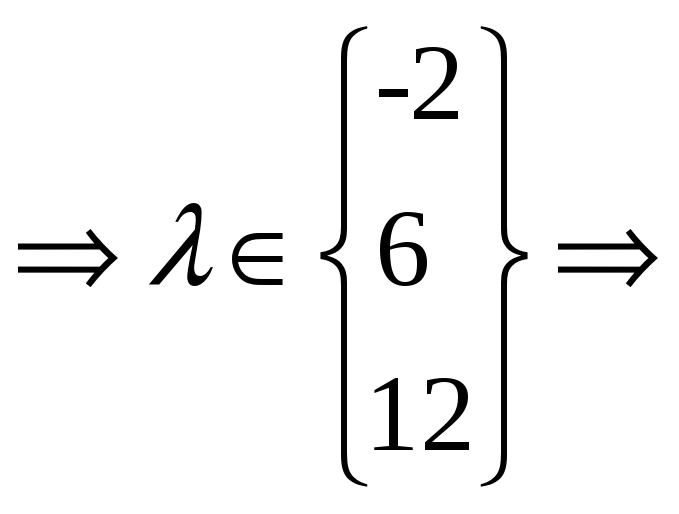 - собственные числа матрицы А

Теперь найдем собственные векторы.

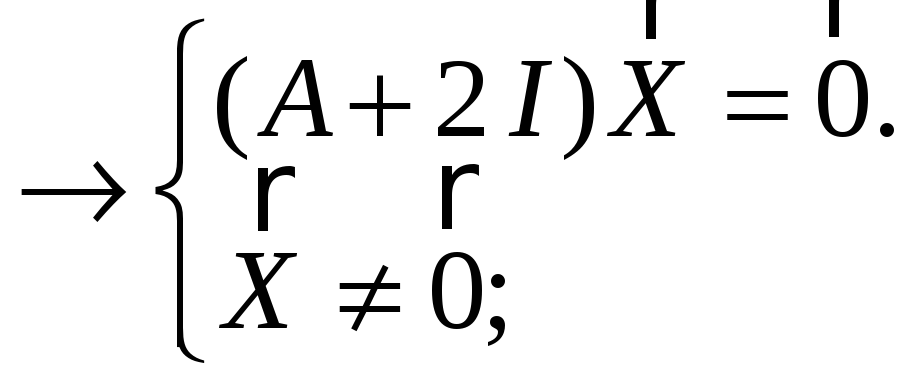
a

b

c

===

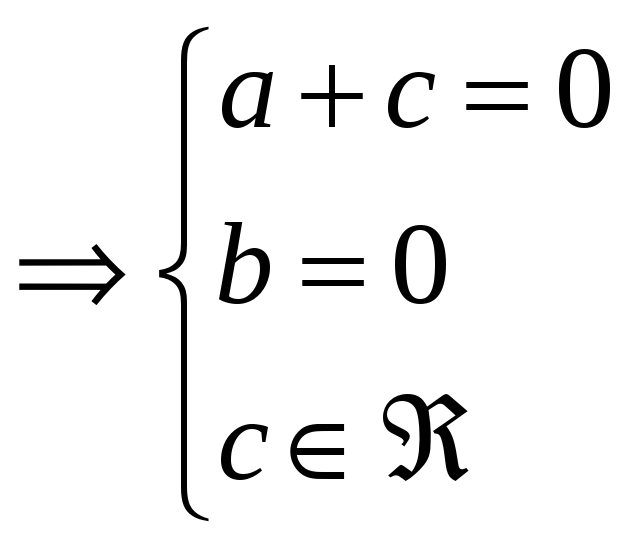
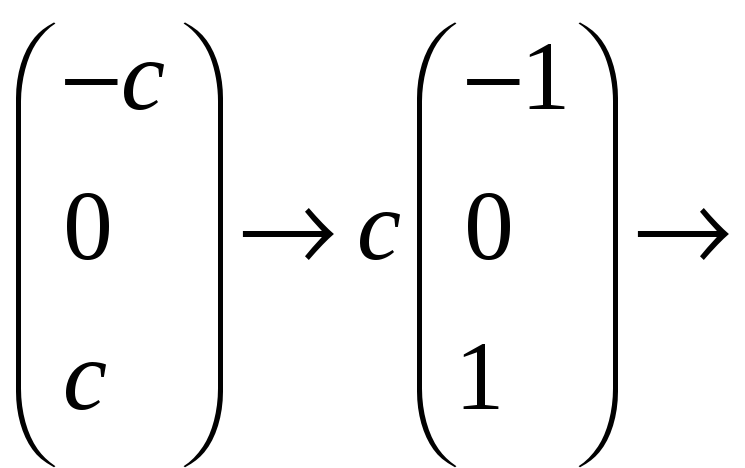
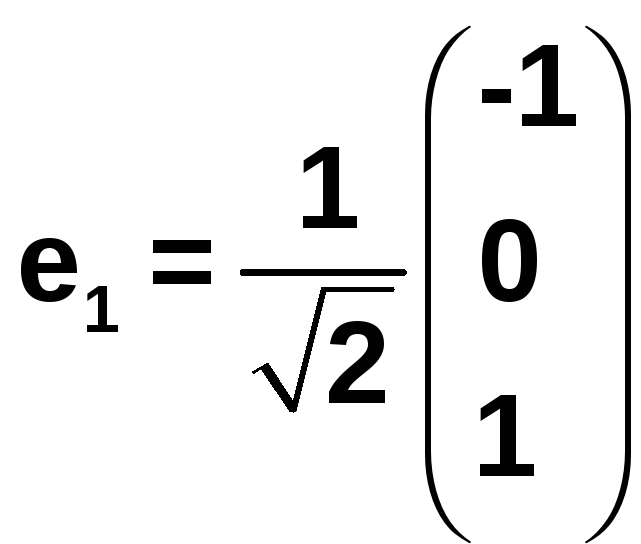
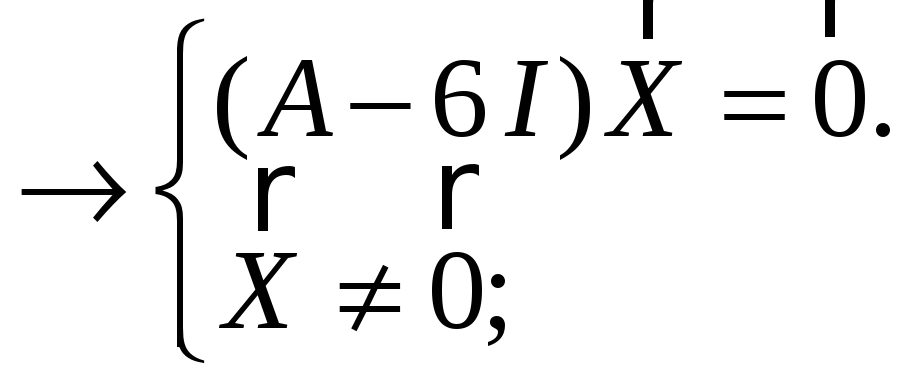
a

b

c

===

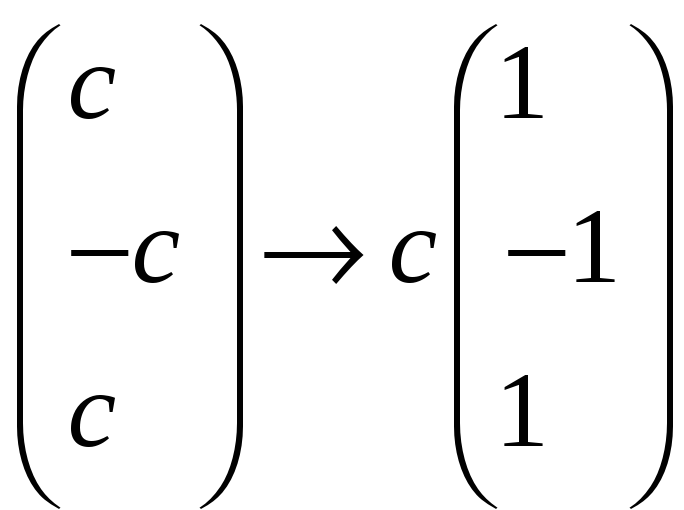
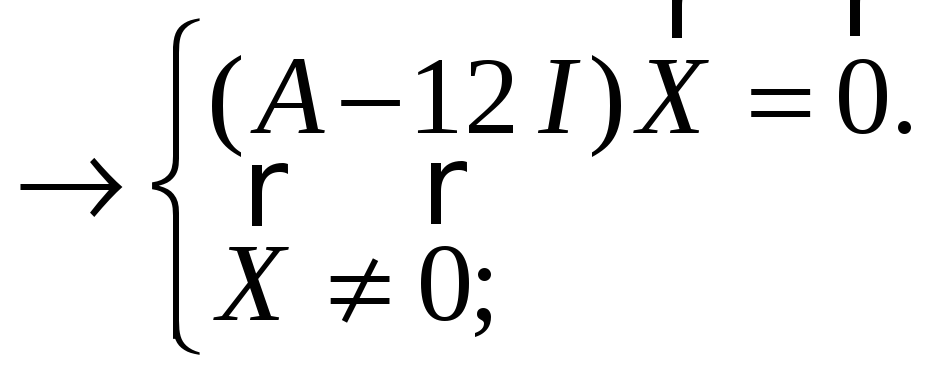
a

b

c

===

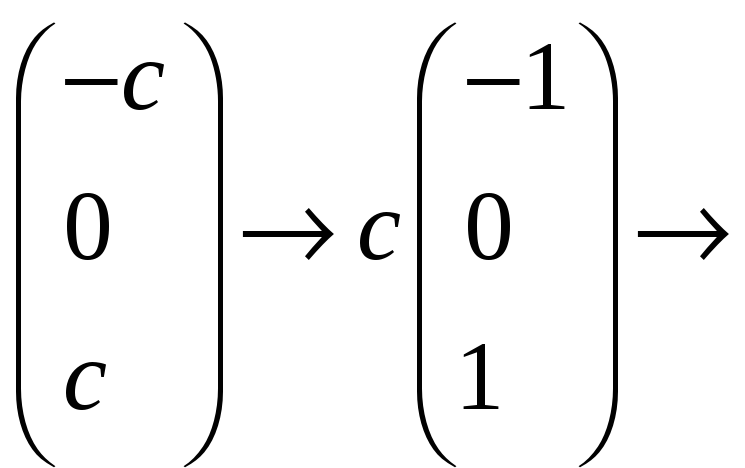
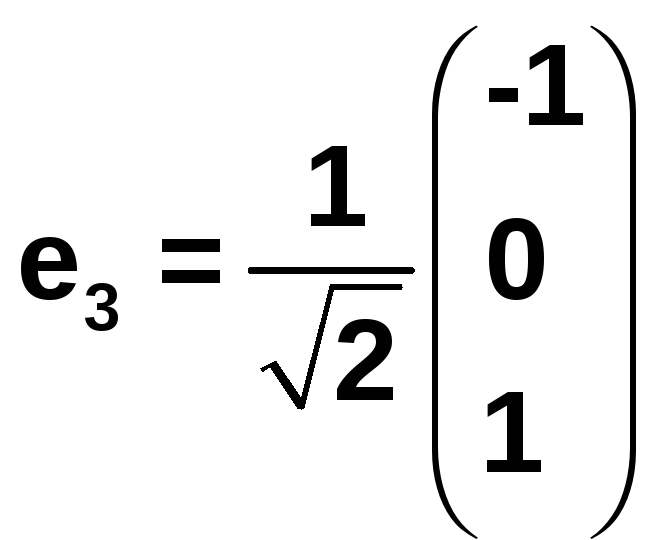
(3)

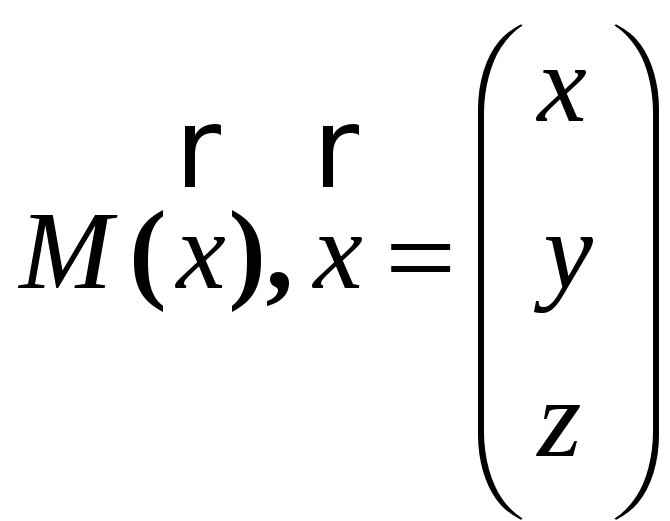
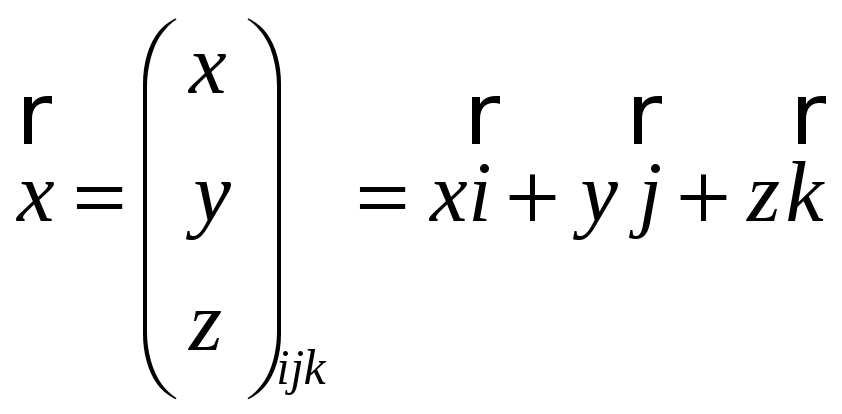
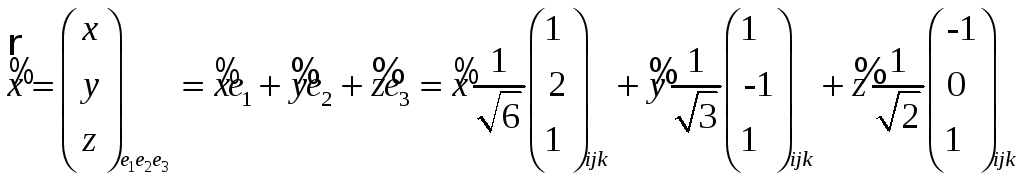вернулись в стандарт. базис (1)

Приравняем векторы и настроим связь координат старого и нового базисов

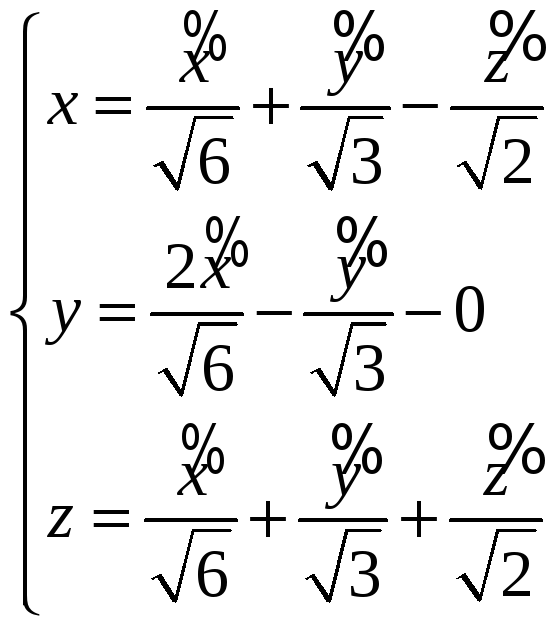подставили в элемент каждого собств. вектора в формуле (1)

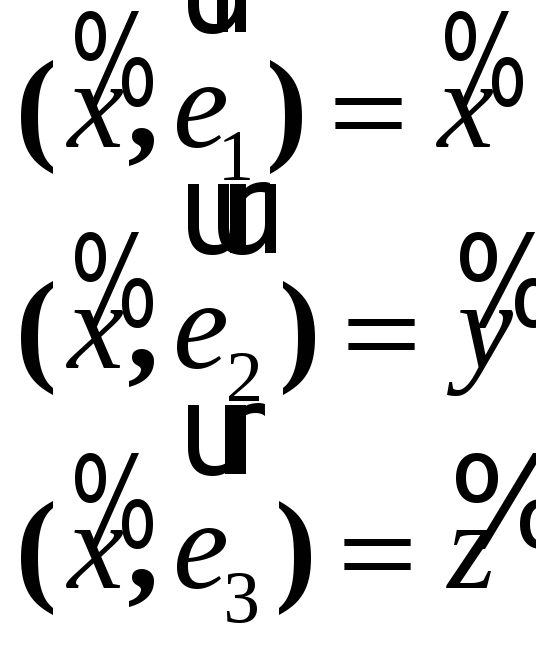подставили в (3)

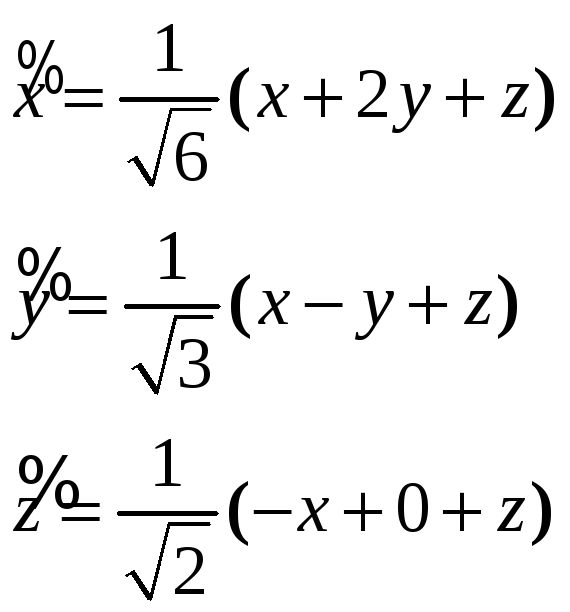
б) Привести уравнение кривой второго порядка к каноническому виду и изобразить ее на координатной плоскости

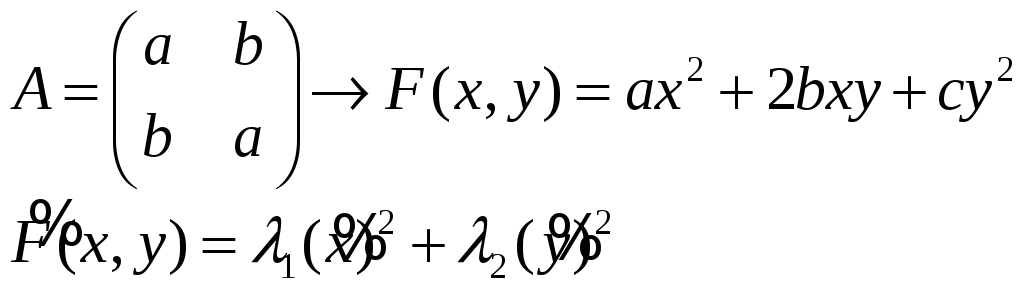
1) Найдем собственные числа и векторы

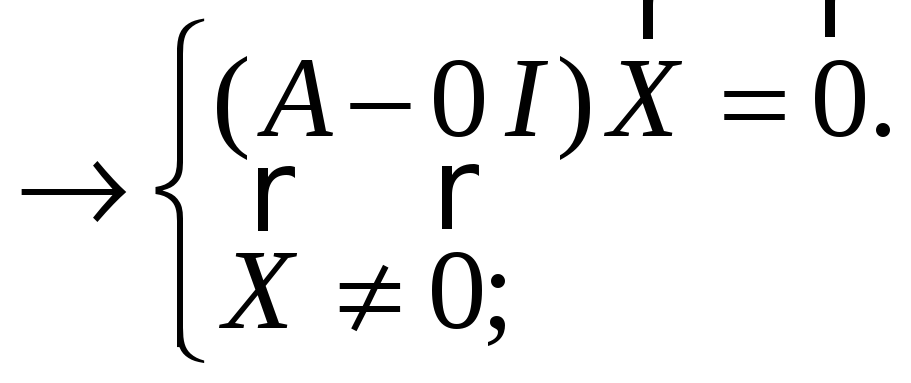
a

b

==

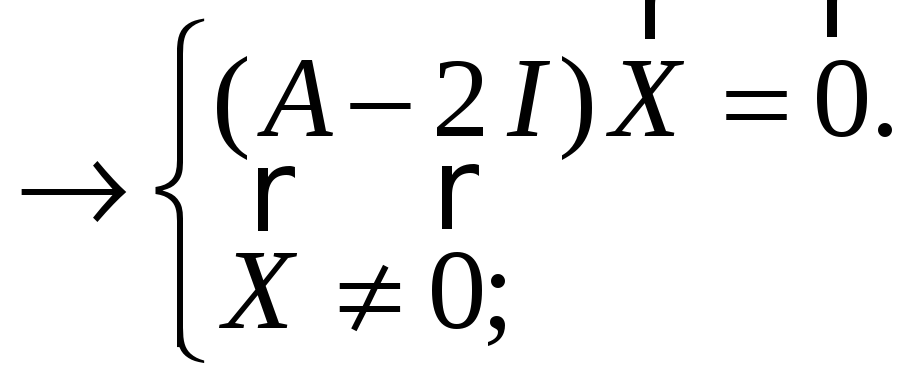
a

b

==

2) Введем систему координат по которой направим оси и

Точка

Запишем связь координат

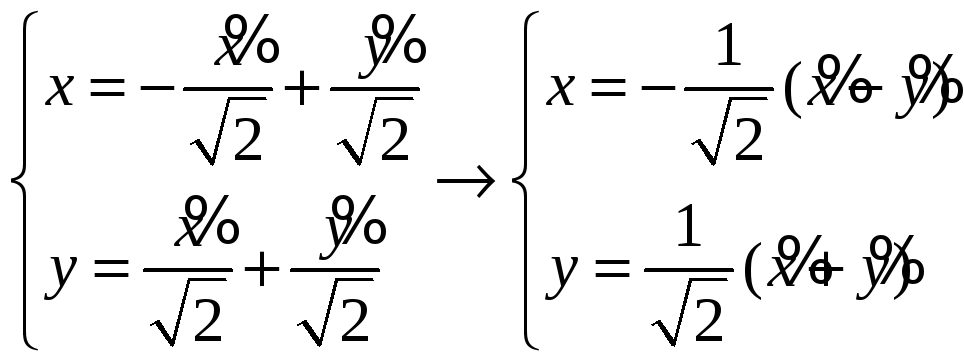Из разложения вектора по базису

Старые координаты подставим в исходное уравнение и запишем это уравнение в новых координатах
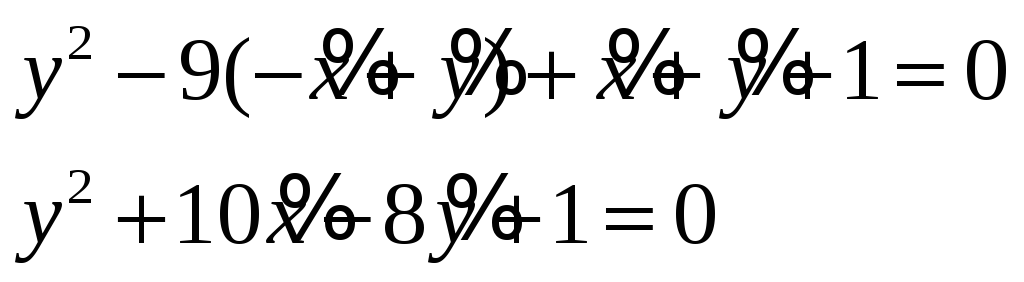