§6 Определитель матрицы.

Пусть А_m- квадратная матрица порядка “m”, и a_ik – элемент “i”- строки и “k”- столбца матрицы; I,k=1..m. Вычеркнем из матрицы А “i”- строку и “k”- столбец и назовем полученную матрицу “m-1”- порядка дополнительной матрицей элемента a_ik.

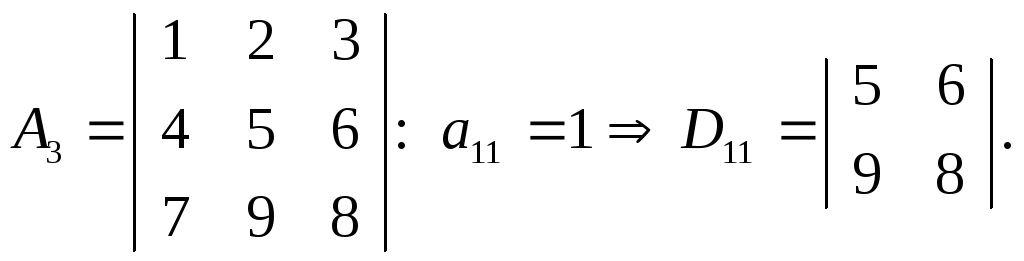
Определение-1. Определителем матрицы второго порядка называется число

detD₁₁=40-54=-14;

Определение-2. Алгебраическим дополнением A_ik элемента a_ik называется число

A_ik=(-1)^I+kdetD_ik;  A₁₁=(-1)²detD₁₁=-14

Обратите внимание на «достойное удивления» свойство алгебраических дополнений элементов матрицы: суммы произведений элементов любой строки или любого столбца матрицы на их алгебраические дополнения равны между собой !!!

Определение-3. Определителем матрицы порядка “m>2” называется число

,

равное сумме произведений элементов (любой) строки или столбца (любого)на их алгебраические дополнения. 

Следствия.

1) Определение-3 дает рекуррентный алгоритм вычисления detA_m: определитель матрицы порядка “m” выражается через “m” определителей матриц порядка

“m-1”через m(m-1) определителей матриц порядка “m-2” …  через

m(m-1)(m-2)..2=m! определителей матриц второго порядка, которые определены ЯВНО.

2) Вычислять detA следует по той строке или столбцу, которые имеют наибольшее количество нулевых элементов:

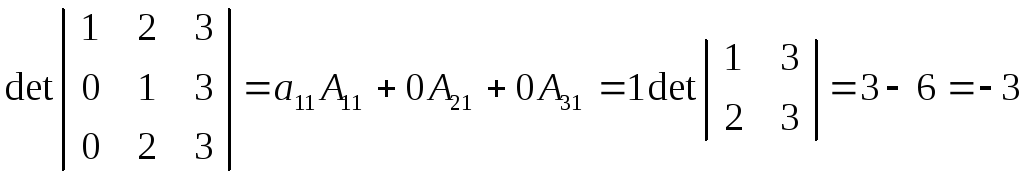
§7. Свойства и вычисление определителей.

EMBED Equation.3

Свойства определителя матрицы .

1. detA^t=detA

2. Определитель «треугольной» матрица (все под- или над-диагональные элементы равны нулю) равен произведению ее диагональных элементов.

EMBED Equation.3

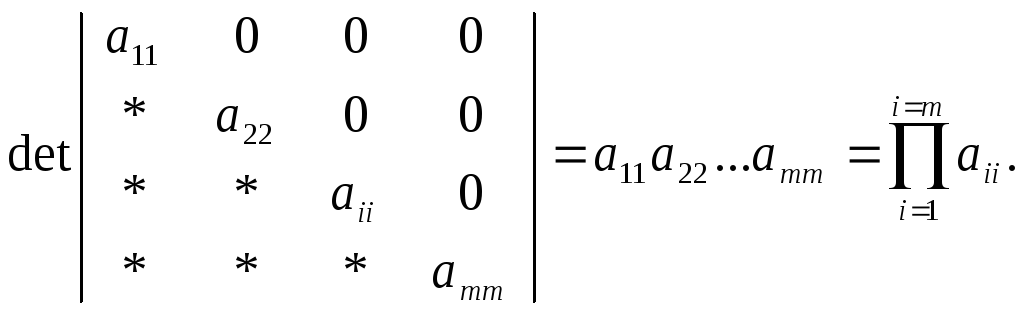
3. Определитель матрицы с "нулевой" строкой или столбцом равен нулю;

4. detA # 0 ==>алгебраические дополнения элементов любой строки или любого столбца не равны нулю одновременно.

5. (без док.) det(P_ikA)= - detA. При перестановке строк (столбцов) матрицы ее определитель умножается на -1. ==> Определитель матрицы с двумя одинаковыми строками (столбцами) равен нулю: Доказательство:

6. det(M_i(λ)A)=λdetA. При умножении строки (столбца) матрицы на число ее определитель умножается на это число :

==> det(λA_m)=λ^mdetA.

7. (без док.)det(S_ik(λ)A)=detA.- Определитель матрицы не изменится, если к ее строке прибавить другую строку, умноженную на число.

Замечание.Если в методе Жордана-Гаусса , свойства (5,6,7) позволяют вычислить определитель начальной (квадратной !!) матрицы СЛАУ.

Например, M₁(λ)P₃₄S₂₃(μ)A=I det[M₁(λ)P₃₄S₂₃(μ)A]=detI=1=λ(-1)detA detA=-1/λ.

Способы вычисления detA_m.

1. 

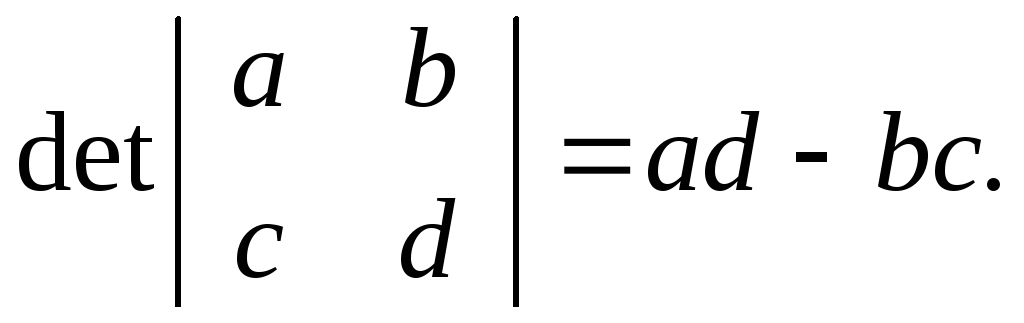
2. detA₃= "правило Саррюса"= (сумма произведений элементов в вершинах треугольников, сторона которых параллельна главной диагонали) – (сумма произведений элементов в вершинах треугольников, сторона которых параллельна другой диагонали)

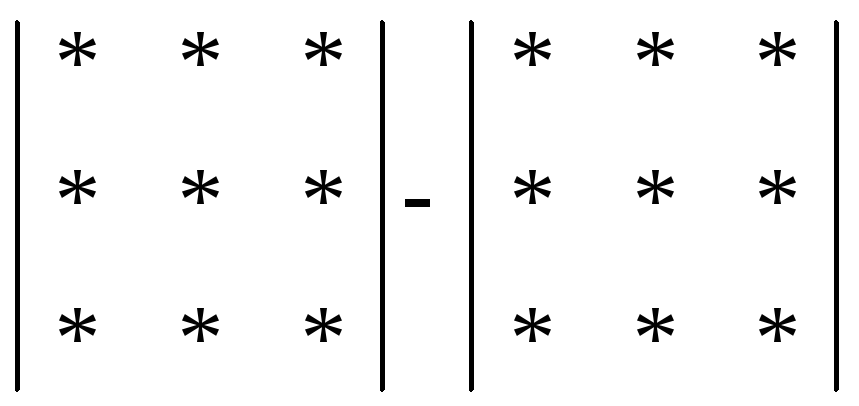
detA= (+) ( - )

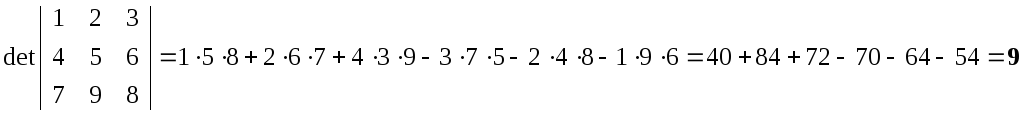
3) Приведение матрицы к треугольному виду – обнуление всех элементов с одной стороны диагонали с помощью операций S_ij(λ).

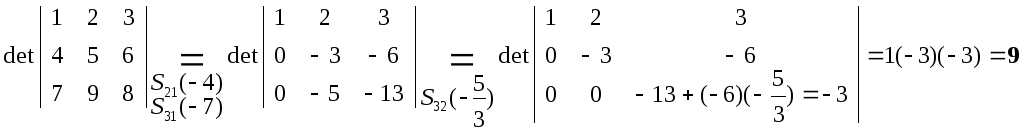
§8. Теорема и формулы Крамера.

Запишем квадратную матрицу в виде ее столбцов:

_{Лемма. Сумма произведений элементов любой строки (любого столбца) матрицы на алгебраические дополнения другой строки (столбца) равно нулю:}

_{Док-во. Рассмотрим матрицу B с двумя одинаковыми столбцами BI=BJ, полученную из матрицы А заменой ее j-столбца i-столбцом:}

A_m=[A1,…,AI,..,AJ,..Am]B=[A1,…,AI,…,BJ=AI,…AM] EMBED Equation.3

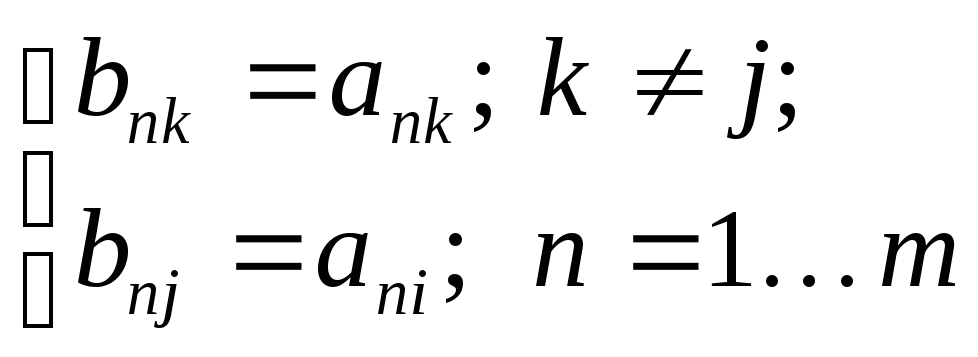
_{Из свойств определителей следует, что detB=0. С другой стороны, "по построению": элементы j-столбца bnj=anj, а их алгебраические дополнения Bnj=Ani}

Поэтому:

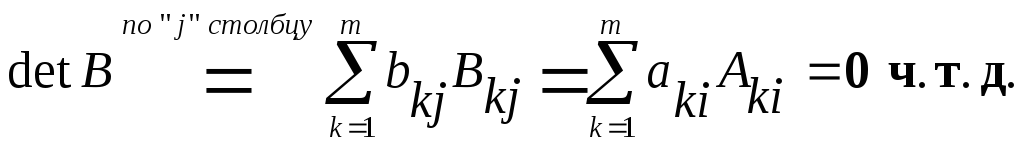
_{!! Свойство алгебраических дополнений квадратной матрицы : "Сумма произведений элементов любой строки или столбца матрицы на "свои" алгебраические дополнения равна определителю матриицы, а на "чужие" - равна нулю !!!}

---------------------------------------------------

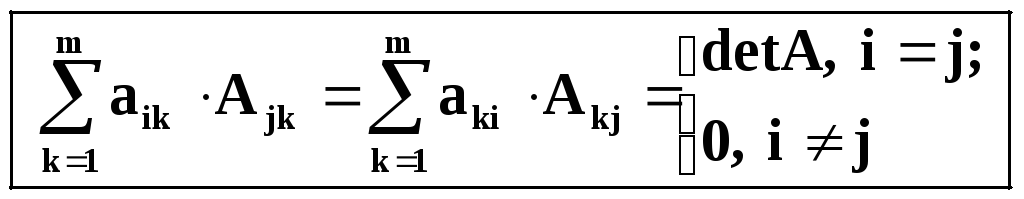
Теорема Крамера. "Если определитель матрицы системы "m" линейных алгебраических уравнений с "m" неизвестными не равен нулю, система имеет единственное решение".

Док-во выполним на примере "m=3":

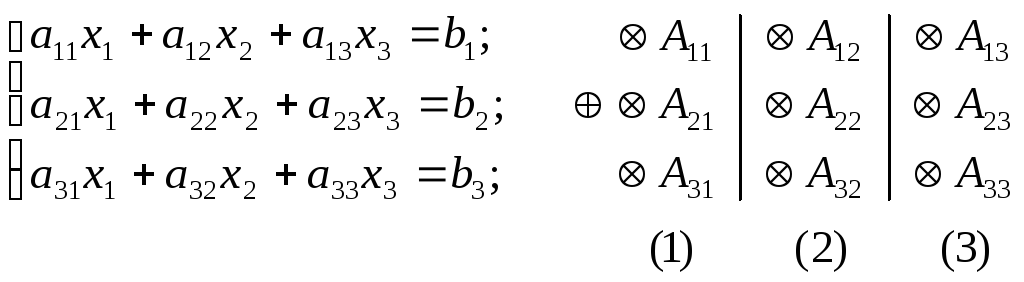
(1) Умножим каждое уравнение системы на алгебраическое дополнение соответствующего элемента первого столбца А _i1 (i=1,2,3) и "сложим" полученные уравнения

EMBED Equation.3

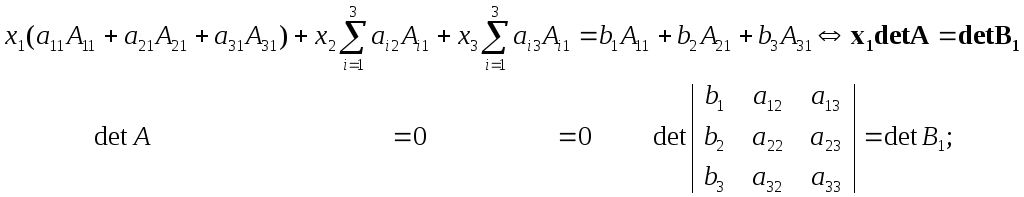
_{(2), (3) -"-"-"-' второго и третьего столбцов -"-"-".}

Так как detA # 0, все алгебраические дополнения столбца одновременно не равны нулю. Поэтому в результате (1),(2),(3) получим равносильную СЛАУ

EMBED Equation.3

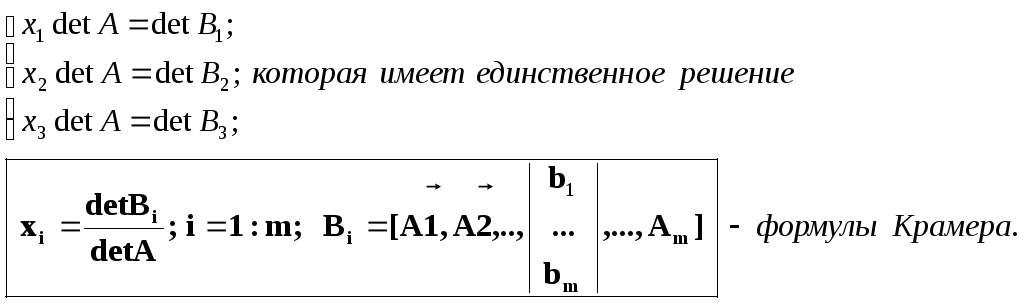
Замечания.

1. Матрица B_i получается из матрицы А заменой ее "i" столбца столбцом из "правых частей" уравнений системы.

EMBED Equation.3

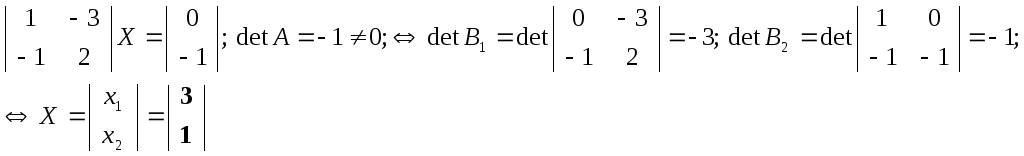
2. Теорема и формулы Крамера применимы только для "квадратных" систем "m" уравнений с "m" неизвестными.

3. На практике формулы Крамера при решении СЛАУ "разумно" использовать лишь для "m<4"; при "m≥4" решать систему следует методом Жордана-Гаусса.

Следствия из т. Крамера.

1) EMBED Equation.3

2) Однородная система линейных алгебраических уравнений AX=0 (с нулевой правой частью) не бывает несовместной : она ЛИБО имеет единственное нулевое решение, если detA#0, ЛИБО имеет множество решений, включая нулевое.

=========================================================================

МУ АХ=ВСЛАУ : 1)неstop;



2)!;

3)Метод? (как найти?).