§4. Метод Жордана-Гаусса (метод полного исключения) решения слау.

Методом Жордана-Гаусса (методом полного исключения) называется алгоритм, в результате работы которого через конечное число «шагов»- равносильных преобразований либо обнаруживается несовместность системы (Х=), либо в явном виде находится множество ее решений, при этом РМ системы РМ=|A_mxn|B_nx1| приводится к одному из трех видов: , а на месте матрицыВ –вектор-столбец – единственное решение СЛАУ.

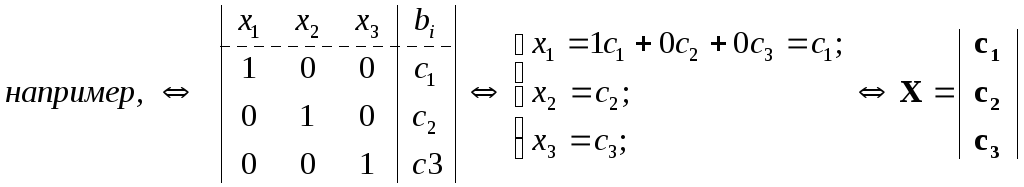
[II] РМ: m<n и в левой части РМ получается единичная матрица I_m размерности m<n и дополнительная матрица A1_mx(n-m), элементы которой – коэффициенты при переменных x_m+1,x_m+2,…,x_n: 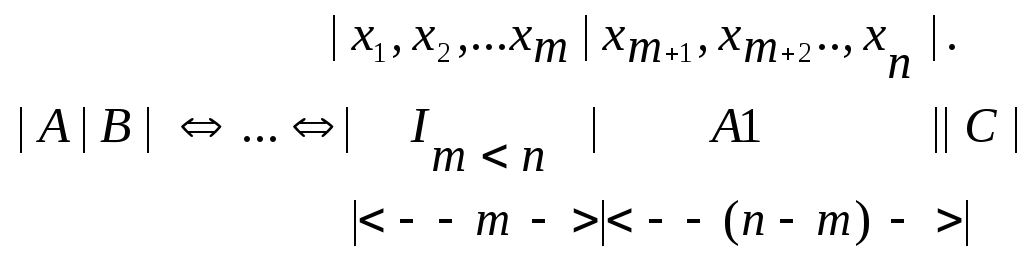. В этом случае “m” неизвестных (x₁,x₂,…,x_m) выражаются через остальные “n-m” неизвестных, которые могут принимать любые значения – x_i>mC.Следовательно, такая СЛАУ имеет бесконечное множество решений.

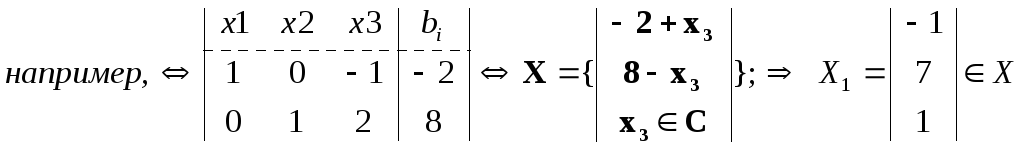
[III] Если в расширенной матрице появляется строка вида [0 0…0|0], соответствующее уравнение системы и следовательно система решений не имеет : Х=(несовместная СЛАУ).

----------------------------------------------------------------

Экз. вопрос. Какие из вариантов множества решений СЛАУ возможны и какие не возможны ,если: (а) m>n ? (б) m=n ? (в) m<n ?

------------------------------------------------------------------

Замечания.

1. Если в процессе работы алгоритма в РМ появляется «нулевая строка» , она удаляется из РМ (количество строк уменьшается на единицу).

2. «Стратегия» метода Ж.-Г. заключается в последовательном преобразовании первого, второго,… столбцов левой части РМ к виду:

3. «Тактика» этой стратегии – «пошаговое» k=1,2,… обнуление всех недиагональных элементов (ik: a_ik0) сначала первого, затем второго и т.д. … столбцов левой части РМ с помощью равносильных преобразований P_ij,M_i(),S_ij().

4. !! На “k”-ом «шаге» (к=1,2,…):(a) диагональный элемент a_kk преобразуется в единицу (M_k(1/a_kk) a_kk 1)и затем недиагональные элементы “k” столбца обнуляются с помощью “k”строки(ik S_ik(-a_ik): a_ik0).

В результате этих преобразований «к»-столбец преобразуется к виду

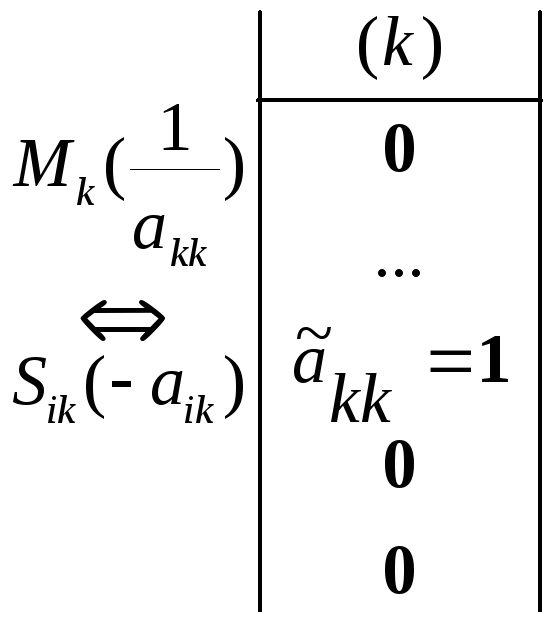
Проиллюстрируем алгоритм метода на трех примерах.

Пример 1. m=n=3.

Пример 2. m=2<n=3.

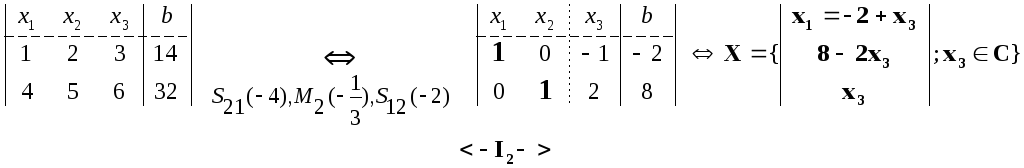
Пример 3. m=3>n=2. Проделайте подробно:

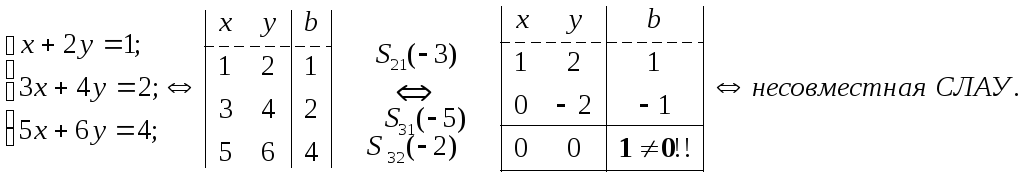
Тр-1.6 «Решение матричных уравнений».

Задание.

Часть 1. 1. Определить размерность матрицы Х в уравнении А1Х=С1 и записать ее явный («буквенный») вид.

2. Методом Ж-Г решить матричное уравнение XA1=C, используя тождества

3. Методом Ж-Г найти матрицу B2^-1, обратную к В2, решив уравнение В2Z=I <=> Z=B2^-1.

Часть 2. 1. Вычислить detB2.

2. Используя решение Х уравнения XA1=C1, найти матрицу D=C2 - A2X.

5. 3. Методом обратной матрицы решить уравнение B2Y=D.

6. 4. Показать, что матрицы Х и У являются решением системы матричных уравнений

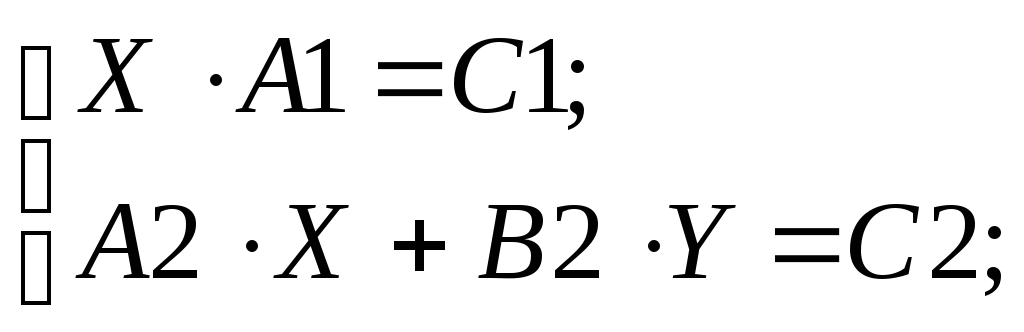
7. Условие ТР содержит матрицы А1_3х4, С1_3х4, А2_4х3, В2_4х4, С2_4х3 и номер варианта:

   A13х4	C13х4	A24х3	B24х4	C24х3
   Вар.

9. Пример.

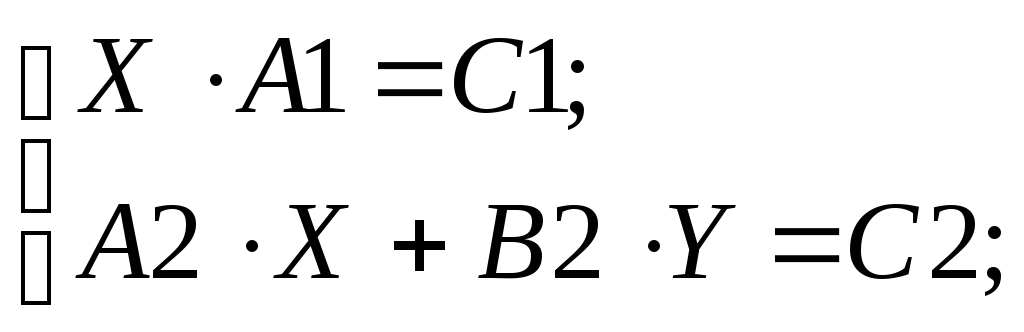
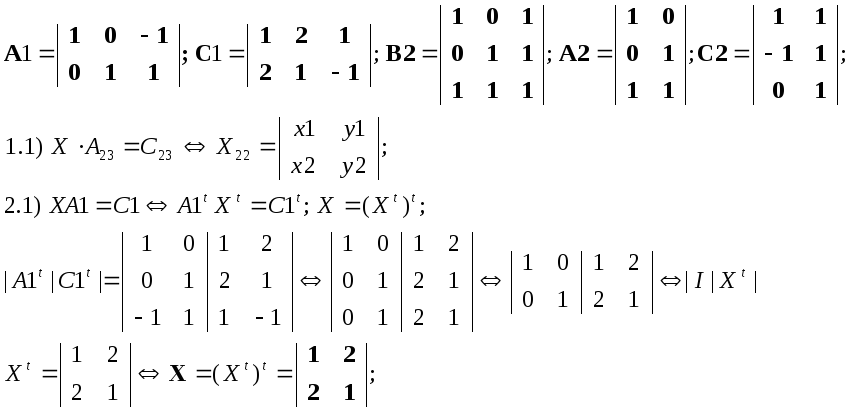
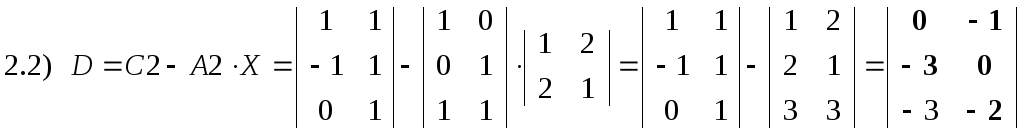
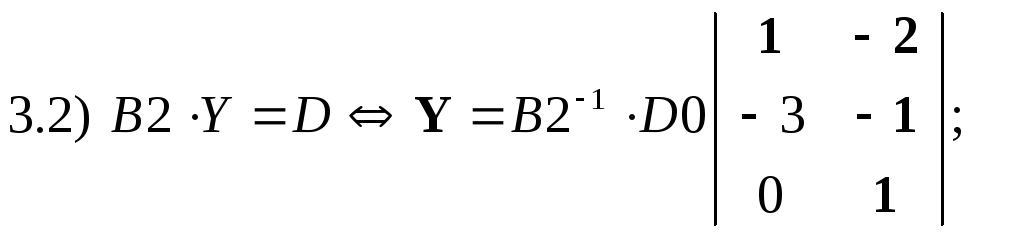
4.2)

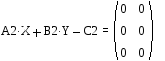
Вариант Тр.

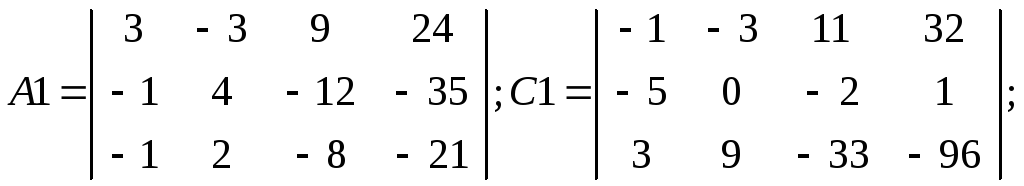
§5. Матричные уравнения. Обратная матрица.

Пусть заданы числовые матрицы A_mxn, B_{mxk .}

Определение. Числовая матрица X соответствующей размерности называется решением матричного уравнения AX=B (ХА=В), если она обращает уравнение в верное равенство числовых матриц.

Например,

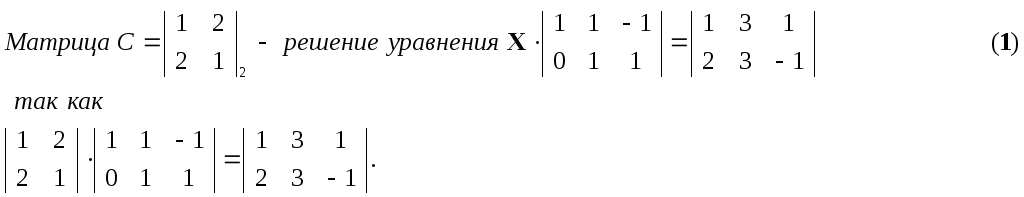
Рассмотрим уравнение AY=B

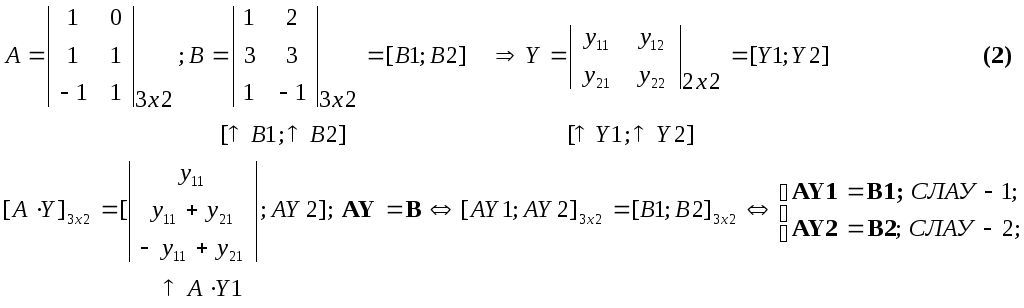
В общем случае, матричное уравнение A _mxnX =B_mxk равносильно совокупности “k” СЛАУ с одинаковой матрицей A. Решать эти системы методом Жордана-Гаусса следует одновременно, записав «обобщенную» расширенную матрицу с “k” правыми частями РМ =[A |B1;B2;..; Bk].

Замечания.

1.Если в процессе работы по алгоритму Ж-Г:

• в РМ появляется “нулевая строка” [0,0,…,0|0,0,..0], она удаляется из РМ.

• в РМ появляется строка [0,0,…,0|0,b_i#0,..0], равносильные преобразования заканчиваются: матричное уравнение решений не имеет;

• РМ приводится к виду [I_n|b₁;b₂;…b_k],система имеет единственное решение: Y=B=[ b₁;b₂;…b_k];

2. Матричное уравнение ХА=B «не приспособлено» к методу Ж-Г; Алгоритм его решения такой: (а) сначала уравнение транспонируется , (б)затем методом Ж-Г решается уравнение и (в) полученный результат транспонируется:

Примеры.

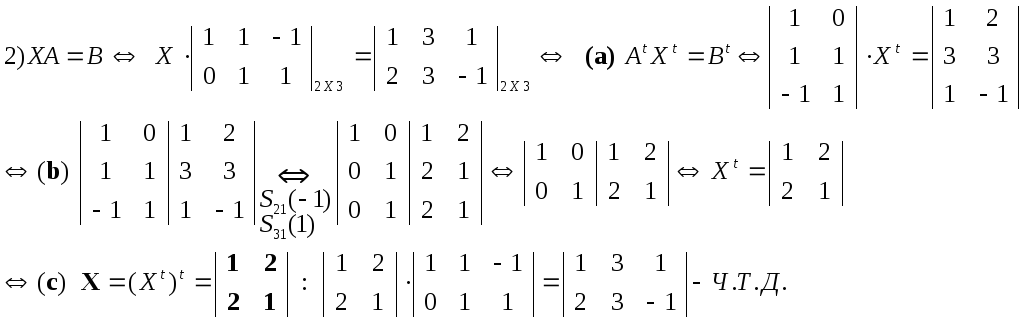
Пусть задана квадратная матрица A_m.

Определение.

Матрица А^-1 называется обратной матрицей для матрицы А, если АА^-1 =I.

Следствия.

1. Матрица имеет обратную, если существует решение матричного уравнения

2. Находится обратная матрица методом Ж-Г : [ A | I ] <==> [ I | A^-1 ].

Можно показать, что квадратная матрица А одновременно имеет (или не имеет) «левую» А^-1_лев (А^-1_левA=I) и «правую» А^-1_пр (A А^-1_пр=I) обратные матрицы и они равны А^-1_лев= А^-1_пр; поэтому в дальнейшем будем обозначать A^-1.

3. Если известна обратная матрица A^-1, решения матричных уравнений AX=B и XA=B находятся методом обратной матрицы: обе части уравнения умножаются на A^-1 «слева» или «справа», соответственно.

Например, Для - проверьте, чтоA^-1A=I !!

Тогда,