Эмпирический материал обширный по объему

Эмпирический материал ограниченного объема

Эмпирическое распределение

Эмпирическое распределение

Определение числовых характеристик эмпирического распределения

Выдвижение гипотезы о предполагаемом теоретическом законе распределения

Оценка неизвестного параметра теоретического распределения

Проверка гипотезы согласованности предполагаемого теоретического распределения с эмпирическим

Определение точности оценки

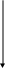
Принятие или отклонение гипотезы о виде теоретического распределения

Параметр теоретического распределения

Теоретическое распределение

Рисунок 4  Модуль 3: Анализ результатов опыта (эмпирического

материала), описываемого одной случайной величиной

На основе анализа опытных данных решаются следующие задачи: определение закона распределения случайной величины (рису- нок 4) или системы случайных величин (рисунок 5) по статистическим данным, проверки правдоподобия гипотез, нахождение неизвестных параметров распределения, сглаживание статистических данных.

Рисунок 5 – Модуль 4: Анализ результатов опыта (эмпирического

материала), описываемого системой случайных величин

Для успешного изучения курса студенту необходимо знать основы дискретной математики (элементы теории множеств и комбинаторику), математического анализа (дифференциальное и интегральное исчисление функции одной и нескольких переменных).

Курс теории вероятностей и математической статистики является базовым при изучении таких дисциплин, как «Вычислительная математика», «Интеллектуальные информационные системы». Вопросы, рассматриваемые в данном курсе, получат в дальнейшем развитие при

изучении статистического моделирования на ЭВМ, при оценке точности и достоверности результатов моделирования, при осуществлении имитационного моделирования информационных систем и сетей; при расчете надежности информационных систем; при разработке модели прикладных процедур, реализующих правила обработки данных и др.

Курс имеет практическую часть (практические занятия – 17 ч), на самостоятельную работу студентов при изучении дисциплины отводится 51 час.

Итоговая аттестация знаний студентов осуществляется во время экзамена, в конце семестра.

2 Методические рекомендации по изучению дисциплины

Учебным планом по дисциплине «Теория вероятностей и математическая статистика» для студентов предусмотрено участие в лекцих, практических занятиях, выполнение типового расчета и аудиторной контрольной работы. Завершающим этапом изучения дисциплины является сдача экзамена.

1. Лекции и практические занятия

Основной составной частью учебного процесса в преподавании теории вероятностей и математической статистики студентам дневной формы обучения являются лекции и практические занятия. В БТИ посещение занятий является обязательным. Студенты, активно участвующие в лекционных и практических занятиях, способны успешнее освоить предмет.

Все лекции студентам необходимо конспектировать. В конспект рекомендуется выписывать определения, формулировки и доказательства теорем, формулы и т.п. На полях конспекта следует отмечать вопросы, выделенные студентом для консультации с преподавателем, а также вопросы, вынесенные преподавателем на самостоятельное изучение. Выводы, полученные в виде формул, рекомендуется в конспекте подчеркивать или обводить рамкой, чтобы при перечитывании конспекта они выделялись или лучше запоминались. Полезно составить краткий справочник, содержащий важнейшие и наиболее часто употребляемые формулы дисциплины. К каждой лекции следует разобрать материал предыдущей лекции.

На практических занятиях подробно рассматриваются основные вопросы дисциплины, разбираются основные типы задач по теории

вероятностей и математической статистике. К каждому практическому занятию следует заранее самостоятельно выполнить домашнее задание и ознакомиться с материалом лекций к следующей теме. Систематическое выполнение домашних заданий является важным фактором, способствующим успешному усвоению дисциплины.