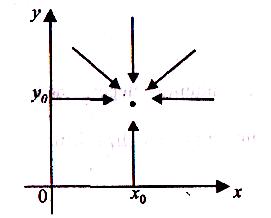
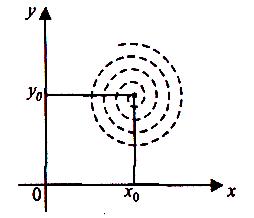
- •“Диференціальне числення функції багатьох змінних”
- •Означення функції багатьох змінних
- •Способи задання функції
- •Неперервність функції двох змінних
- •Диференційовність функції двох змінних
- •Частинні похідні і повні диференціали вищих порядків
- •Знаходження найбільшого та найменшого значень неперервної функції на замкненій обмеженій множині
Способи задання функції
Як і функцію однієї змінної, функції двох змінних можна зобразити: — аналітичнo (у вигляді формули), наприклад:
![]()
таблично (у вигляді таблиці), наприклад:
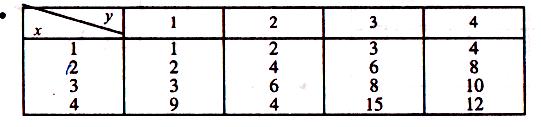
— графічно.
Для
графічного зображення функції двох
змінних необхідна система координат
![]() у
тривимірному просторі (мал.1). Кожній
парі чисел х
та
у
відповідає
точка
у
тривимірному просторі (мал.1). Кожній
парі чисел х
та
у
відповідає
точка
![]() площини
площини
![]() .
В точці
прово-
димо
пряму перпендикулярну до площини
.
В точці
прово-
димо
пряму перпендикулярну до площини![]() ,
та відмічаємо на ній відповідне значення
функції z;
дістаємо в просторі точку Q
з
координатами
,
та відмічаємо на ній відповідне значення
функції z;
дістаємо в просторі точку Q
з
координатами
![]() ,
яка позначається символом
,
яка позначається символом
![]() . Точки Q,
які
відповідають різним значенням незалежних
змінних, складають певну поверхню у
просторі. Така поверхня є
. Точки Q,
які
відповідають різним значенням незалежних
змінних, складають певну поверхню у
просторі. Така поверхня є
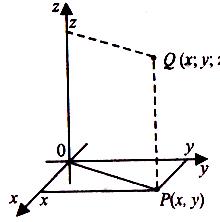 графічним зображенням функції
графічним зображенням функції
![]() .
.
Мал.1
Зауваження: На практиці побудувати графік функції важко, адже йдеться про зображення на площині просторової фігури, а це не завжди вдається.
• Графічне
зображення функції
![]() є площина, яка проходить
є площина, яка проходить
через
точки
![]() ,
,
![]() ,
,
![]() (мал.2).
(мал.2).
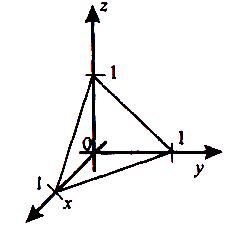

Мал.2 мал.3
Геометричне
зображення функції![]() є
півкуля (мал.3).
є
півкуля (мал.3).
Існує й інший спосіб геометричного зображення функції двох змінних — зображення за допомогою ліній рівня.
Означення:
Лінією
рівня називається
множина всіх точок площини, в яких
функція
![]() набуває
однакових значень.
набуває
однакових значень.
Рівняння
ліній рівня записують у вигляді
![]()
Накресливши кілька ліній рівня та зазначивши, яких значень набуває на них функція, одержимо наближене уявлення про зміну функції. Елементарний приклад зображення функції за допомогою ліній рівня-зображення рельєфу місцевості на географічній карті. Висота місцевості над рівнем моря є функцією координат точки земної поверхні. За лініями рівної висоти, нанесеними на карту, легко уявити собі рельєф даної місцевості.
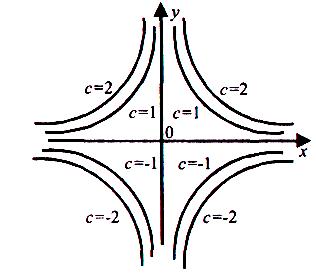
Приклад : Побудувати лінії рівня функції z = x2y
• Рівняння
ліній рівня має вид
![]() або
або
![]() .
.
Покладаючи С = 0, ± 1,±2,..., одержимо сім'ю ліній рівня :
Знаходження області визначення функції двох змінних
Покажемо алгоритм знаходження області визначення функції двох змінних на прикладі.
Приклад
1:
Знайти
область визначення функції
![]()
та дати їй геометричну інтерпретацію.
• 1. Знайдемо область визначення функції аналітично
![]()
2.
Нерівності в D
замінюємо
рівностями і будуємо лінії, що їм
відповідають на координатній площині,
а саме:
![]() ;
;
![]()
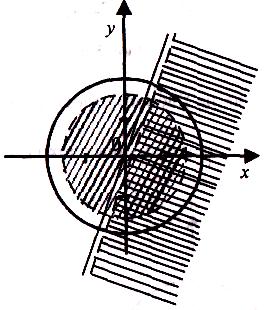
3.
Визначаємо за допомогою контрольних
точок![]() ,
,![]() розташування
D
на
площині і заштриховуємо її (мал.1).
розташування
D
на
площині і заштриховуємо її (мал.1).
![]()
![]()
![]()
Мал.1
![]()
Приклад 2: Знайти область визначення функції двох змінних та дати їй геометри чну інтерпретацію:
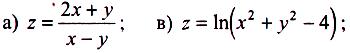
а) Функція невизначена, якщо х = у.
Геометрично це означає, що область визначення складається із двох напів-площин, одна з яких лежить вище, а друга — нижче від прямої у = х
(мал 1).
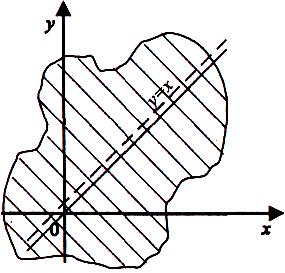
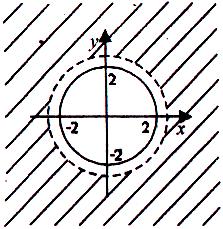
Мал .1 мал.2
в)
Функція визначена, якщо
![]() ,
,
тобто
![]() (мал.2).
(мал.2).
Границя функції двох змінних
Означення:
Число
В
називається
границею
функції
![]() при
при
![]() ,
,![]() ,
якщо для будь-якого
,
якщо для будь-якого
![]() існує
число
існує
число
![]() таке,
що при
таке,
що при
виконанні
нерівності
![]() виконується нерівність
виконується нерівність
![]() і позначається
і позначається
![]() або
або![]()
Зауваження: Для функції багатьох змінних справедливі теореми про границю суми, добутку та частки, які аналогічні відповідним теоремам для функції однієї незалежної змінної
Приклад:
Обчислити
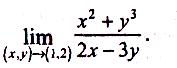
• Використовуючи теореми про арифметичні операції над границями, а також те, що границя постійної дорівнює цій постійній, тобто , маємо
![]()
![]()
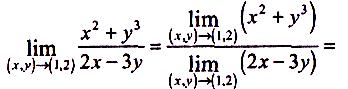
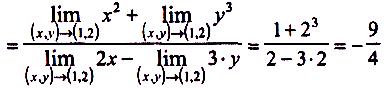
Зауваження: Між поняттями границі в точці для функції однієї змінної та функції багатьох змінних є багато загального, але є й принципова відмінність, яка робить поняття границі функції кількох змінних суттєво більш обмеженим, ніж поняття границі функції однієї змінної.
Справа
в наступному: якщо—
![]() функція однієї змін-
функція однієї змін-
ної), то це означає, що і лівостороння і правостороння границя дорівнює b. Вірно й обернене: з існування та збігу двох односторонніх границь слідує існування границі функції в точці.
Для
функції двох змінних
![]() наближатися
до точки (х0,у0)
наближатися
до точки (х0,у0)
можна нескінченною множиною засобів: і справа, і зліва, і зверху, і знизу, і під кутом 30° до осі тощо