Міністерство освіти та науки України

Бердичівський політехнічний коледж

Волошина З. П.

Методична розробка з дисципліни

“Основи вищої математики”

на тему:

“Диференціальне числення функції багатьох змінних”

для студентів II курсу спеціальностей 5.090227, 5.090246

Розглянуто та схвалено

на засіданні циклової комісії

фізико-хіміко-математичних

дисциплін.

Протокол № від 200

Голова комісії О.О.Горленко.

Бердичів 2006

ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ

ОСНОВНІ ПОНЯТТЯ Множини точок на площині та в п-вимірному просторі

Упорядкованій парі чисел (х₀,у₀) на координатній площині відповідає одна точка P_o(х₀,у₀) . Аналогічно, в n-вимірному просторі п упорядкованим дійсним числам відповідає одна точка P_o(x₁^o,x₂^o,…,x_n^o) де числа x₁^o ,x₂^o,…,x_n^o

будуть координатами цієї точки. З метою скорочення запису далі будемо розглядати множини точок на площині, але дані означення можна вважати вимірними і у випадку n-вимірного простору.

Означення: Множина точок називається зв'язною, якщо будь-які її дві точки можна з'єднати ламаною лінією так, щоб всі точки цієї лінії належали цій множині.

Приклад: На мал.у випадку а) буде зв'язна множина, а у випадку б) не зв'язна.

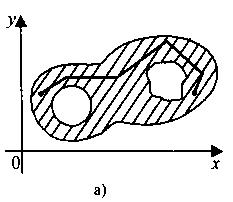
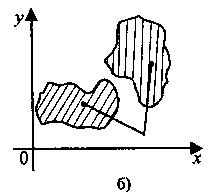
Означення: Множина точок називається обмеженою, якщо її точки належать множині точок круга скінченного радіуса.

Приклад: На мал. у випадку а) маємо обмежену множину, а у випадку б) необмежену.

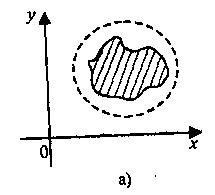
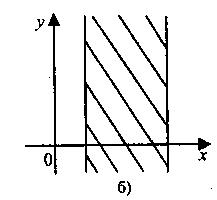
Означення функції багатьох змінних

Означення: Якщо кожній точці множини D

простору поставлено у відповідність з деяким законом одне і тільки одне дійсне число ', то кажуть, що в області задано функцію п

незалежних змінних .

При цьому D називають областю визначення функції, Е — областю значень функції.

Згідно з означенням функцію можна розглядати як

функцію точки і записувати як

В частковому випадку, при кажуть, що задана функція двох змінних , якщо кожній парі на площині підставлено у відповідність

тільки одне число z. Для прикладних питань економіки має значення розгляд функції двох або трьох незалежних змінних. Тому в подальшому більше уваги звертається на ці функції.

Наведемо приклад функції багатьох змінних:

Приклад: Витратами на виробництво даного виробу при даній техніці виробництва є функція матеріальних витрат х і витрат на оплату робочої сили у:

Це є функція витрат виробництва.