3.2 Расчет открытой зубчатой передачи

3.2.1. Проектировочный расчёт открытой цилиндрической прямозубой передачи на выносливость зубьев при изгибе

Открытые передачи рассчитывают только на выносливость зубьев при изгибе , так как абразивный износ поверхностей зубьев происходит быстрее, чем усталостное контактное выкрашивание.

Проектировочный расчёт служит только для предварительного опре-деления размеров. Принимаем материал Сталь 45 ГОСТ 1050-88 со следующими характеристиками: твердость НВ=302, предел прочности G_В =890 МПа, предел текучести G_Т =650 МПа .

Ориентировочное значение модуля m (мм) вычисляют по формуле [1,стр.34]:

(3.1)

где K_m-вспомогательный коэффициент(K_m=14);

T_3F-крутящий момент на валу шестерни(T_3F=1510 H·м);

K_Fβ- коэффициент,учитывающий распределение нагрузки по ширине венца (K_Fβ=1,08) /1,рис.2.1(б)/;

Z₁-число зубьев шестерни(Z₁=17);

Y_F1- коэффициент,учитывающий форму зуба(Y_F1=4,25) ([1],рис.3.3/; ψ_bd – коэффициент ширины зубчатого венца(ψ_bd=0,5) ([1],табл.3.4/;

G_FP1-допускаемые напряжения изгиба зубьев :

G_FP1= Y_S∙Y_R∙K_XF∙G_Flim/S_F, (3.2)

где Y_S – коэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений (принимаем Y_S=1,025 ) (х1ъ,рис.3.1);

Y_R – коэффициент, учитывающий шероховатость переходной поверхности (для шлифования при шероховатости не ниже R_Z40 принимаем Y_R=1,2 );

K_XF – коэффициент, учитывающий размеры зубчатого колеса (принимаем K_XF=1) ([1],рис.3.5);

G_Flim – предел выносливости зубьев при изгибе, соответствующий эквивалент-ному числу циклов перемены напряжений, МПа;

S_F – коэффициент безопасности.

Предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений, МПа определяем по формуле:

G_Flim=G_Flimb∙K_Fа∙K_Fd·K_Fo∙K_F1, (3.3)

где G_Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжеий, МПа ([1],табл.3.4);

K_Fа – коэффициент, учитывающий влияние шлифования переходной поверх-ности зуба (для зубьев с шлифованной переходной поверхностью при улучшении принимаем K_Fа=1,1);

K_Fd – коэффициент, учитывающий влияние деформационного упрочнения или электрохимической обработки переходной поверхности (принимаем K_Fd=1);

K_Fo – коэффициент, учитывающий влияние двухстороннего приложения нагрузки (принимаем K_Fo=1);

K_F1 – коэффициент долговечности (для длительноработающих передач принимаем K_F1=1).

Предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжеий равен ([1],табл.3.4)

G_Flimb1=1,8∙НВ₁=1,8∙302=543,6 МПа;

Тогда предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений равен

G_Flim1=G_Flimb1∙K_Fа∙K_Fd·K_Fo∙K_F1=543,6∙1,1∙1∙1∙1=597,96 МПа;

Коэффициент безопасности определяют по формуле ([1],таб.28,стр.29):

S_F=S'_F∙S"_F, (3.4)

где S'_F – коэффициент, учитывающий нестабильность свойств материала зубчатого колеса и ответственность зубчатой передачи (при вероятности неразрушения 0,99 и улучшении S'_F=1,75 );

S"_F – коэффициент, учитывающий способ получения заготовки зубчатого колеса (при получении заготовки методом проката принимаем S"_F=1,15 ).

Таким образом коэффициент безопасности равен:

S_F=1,75∙1,15=2,0125.

Подставляя численные значения в формулу 3.2, получим:

G_FР=1,025∙1∙1,2∙597,96/2,0125=365,5 МПа;

Подставляя численные значения в формулу 3.1, получим:

Значение модуля округляют до стандартного по ГОСТ 9563-77 ([1],табл.2.4):

m=8

Уточнённый диаметр делительной окружности шестерни :

d_w1=m_n∙z₁=8∙17=85 мм;

диаметр делительной окружности зубчатого колеса :

d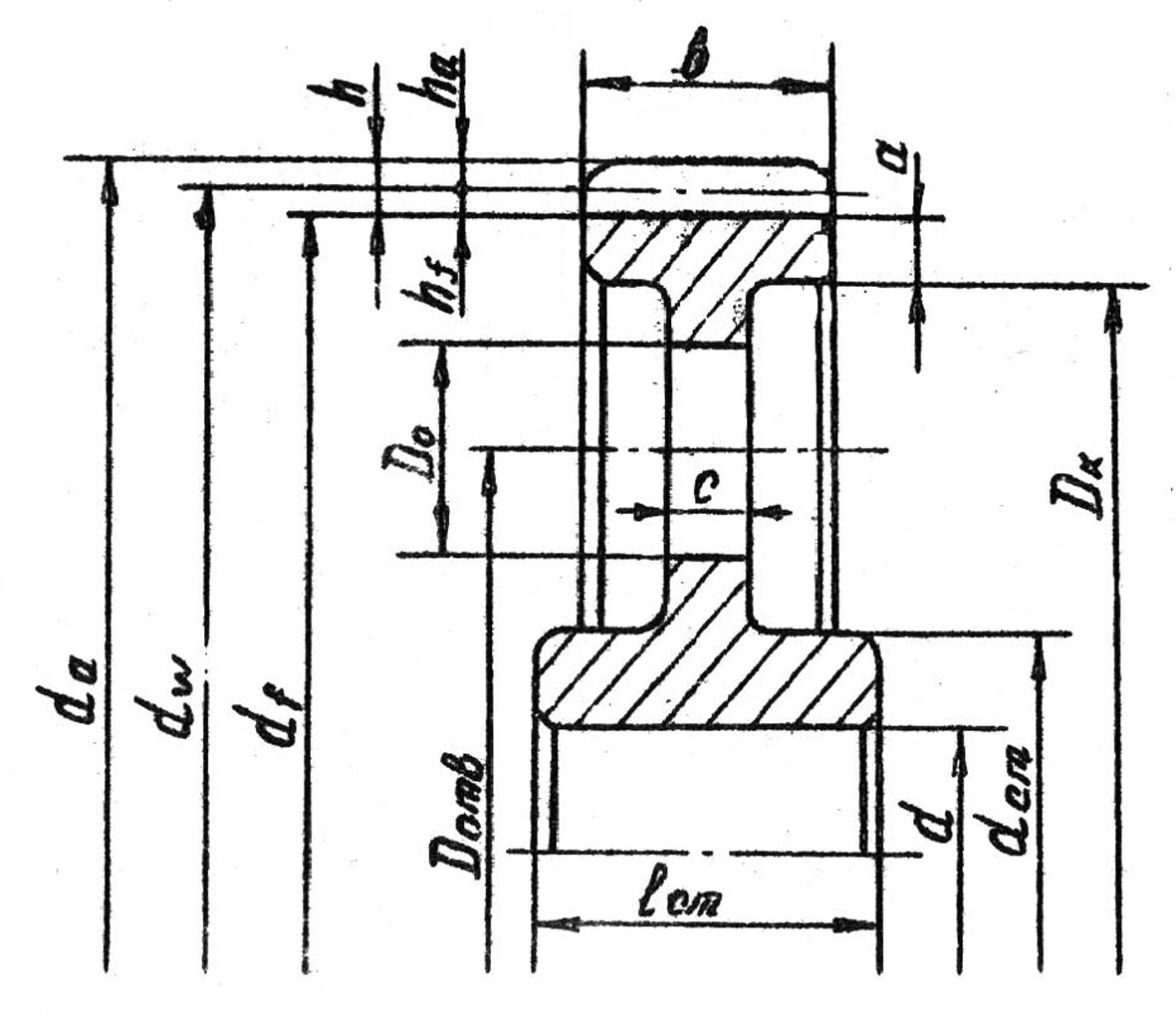 _w2=m_n∙z₂=8∙17·2,92=397,12 мм.

Рмсунок 3.4-Основные параметры цилиндрических зубчатых колес

Уточнённое межосевое расстояние :

а_=(d_w1+d_w2)/2=(136+397,12)/2=266,56 мм.

Окружную скорость определяют по формуле [1,стр.35]:

V=₁∙d_w1/2000, (3.5)

где ₁ – угловая скорость вала шестерни (₁=6,02с^-1);

d_w1 – уточнённый диаметр делительной окружности шестерни(d_w1=136мм).

Подставляем численные значения в формулу 5.5, получаем:

V=6,02∙136/2=0,0,416 м/с.

Для редуктора с цилиндрическими прямозубыми колёсами при расчитанной угловой скорости соответствует восьмая степень точности .

Рабочая ширина венца шестерни равна [1]:

b₁=_bd∙d_w1=0,35∙136=47,6 мм.

3.2.2. Проверочный расчёт зубьев на выносливость при изгибе

Расчётное напряжение изгиба зубьев G_F,МПа, определяют по формуле [1,стр.24]:

G_F=Y_F∙Y_e∙Y_∙W_Ft/m_nG_FР, (3.6)

где Y_F – коэффициент, учитывающий форму зуба (принимаем в зависимости от эквивалентного числа зубьев для шестерни Y_F1=4,26 ) (1,рис.2.3);

Y_e – коэффициент, учитывающий перекрытие зубьев (принимаем, Y_e=1 );

Y_ – коэффициент, учитывающий наклон зуба (Y_=1);

W_Ft – удельная расчётная окружная сила, Н/мм;

m_n – модуль зубчатой передачи, мм;

G_FР – допускаемое напряжение на выносливость зубьев при изгибе, которое определяют раздельно для шестерни и колеса по формуле (1,стр.27)

G_FР=Y_S∙Y_R∙K_XF∙G_Flim/S_F, (3.7)

G_FР=365,5 МПа

Удельную расчётную окружную силу определяем по формуле [1,стр.24]:

W_Ft=2000·K_F∙K_F·K_FV∙T_3F/b∙d_w1, (3.8)

где K_F – коэффициент, учитывающий распределение нагрузки между зубьями (принимаем, что в зацеплении участвует одна пара зубьев, тогда K_F=1 );

K_F – коэффициент, учитывающий распределение нагрузки по ширине венца (принимаем K_F=1,08 ) (1,рис.3.1(б));

K_FV – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении (принимаем K_FV=1,2) ([1],табл.2.6)

T_3F – крутящий момент на валу зубчатого колеса, Н·м;

b – рабочая ширина венца шестерни и зубчатого колеса, мм;

d_w1 – диаметр делительной окружности шестерни, мм,

Подставляя численные значения в формулу 3.8, получаем:

W_Ft=2000·1∙1,08·1,2∙1∙589,49/42,5∙85=422,96

Расчётное напряжение изгиба зубьев равно:

G_F=4,26∙1∙1∙422,96/5=359,55 МПа.

Условие G_FG_FР – выполняется

3.2.3. Усилие в зацеплении

Определение усилий в зацеплении зубчатых колес необходимо для расчета валов и подбора подшипников.

Для прямозубой цилиндрической передачи

Рисунок 3.5.-силы в зацеплении цилиндрических зубчатых колес

Окружная усилие:

(3.9)

где

T – момент на валах колеса и шестерни

dw – диаметр вершин колеса и шестерни

для шестерни: Н

для колеса: Н

Радиальная усилие:

(3.10)

где _w =20^о – угол зацепления

для шестерни: Н

для колеса:

4.РАСЧЕТ ЧЕРВЯЧНОЙ ЗАКРЫТОЙ ПЕРЕДАЧИ С ЦИЛИНДРИЧЕСКИМ ЧЕРВЯКОМ

Червячные передачи рассчитывают на прочность по контактным напряжениям с последующей проверкой зубьев червячного колеса на изгиб как менее прочных по сравнению с витками червяка. Кроме того, после определения размеров корпуса выполняют тепловой расчет червячного редуктора, а также проверочный расчет вала червяка на жесткость.