15.2. Ротатабельное планирование второго порядка

Планирование второго порядка используют в тех случаях, когда линейного приближения недостаточно для математического описания объекта исследований с нужной точностью, а поэтому возникает необходимость в построении моделей в виде полиномов второй степени. При описании поверхности отклика уравнением второго порядка нельзя ограничиться варьированием факторов только на двух уровнях. В связи с этим переходят к планированию, связанному с варьированием факторов на трёх или пяти уровнях.

При ротатабельном планировании второго порядка достраивают план ПФЭ «ядро» или его регулярную дробную реплику (полуреплику) ДФЭ до плана второго порядка добавлением к «ядру» определённого количества «звёздных» и нулевых точек. Матрицу ПФЭ рекомендуется использовать в качестве «ядра» ротатабельного плана второго порядка при к  5, а полуреплику при к  5. Нулевые точки – это точки в центре эксперимента. «Звёздные» точки строят на осях координат, определяя величину «звёздного» плеча L (расстояние от нулевой точки до «звёздной» по оси координат. Для «ядра» в виде плана ПФЭ L определяют по формуле:

. (15.1)

Если ядром является дробная реплика типа 2^к-р, то:

. (15.2)

При выборе числа нулевых точек учитывают, что они необходимы для проверки адекватности модели и оценки ошибки эксперимента.

Общее число опытов N при ротатабельном планировании определяется из соотношения:

N = 2^к + 2к + n₀ = n_я + n_l + n₀. (15.3)

Все данные, нужные для построения матриц ротатабельного планирования при к  7, приведены в табл. 15.2.

На рис 15.1 показано расположение точек относительно центра ротатабельного плана при к = 2 и к= 3. Матрицы ротатабельного планирования второго порядка для к = 2 и к = 3 соответственно показаны в табл. 15.3, 15.4.

При ротатабельном планировании второго порядка обычно велик объём вычислительных работ на стадии обработки экспериментальных данных. Чтобы облегчить расчёты, используют упрощённый вариант для случаев с определённым числом факторов. Уравнения можно записать в следующем виде:

, (15.4)

, (15.5)

, (15.6)

, (15.7)

где – коэффициенты, значения которых выбираются из табл. 15.5.

Рис. 15.1. Расположение экспериментальных точек относительно центра ротатабельного плана

Для оценки значимости коэффициентов регрессии также можно использовать упрощённые формулы (15.8 – 15.13) и соответствующие табличные данные (табл. 15.6).

; (15.8)

; (15.9)

; (15.10)

, (15.11)

где , , , - соответственно квадратичные ошибки в определении коэффициентов ; , , , – коэффициенты.

- ошибка среднего по параллельным наблюдениям, связанная с дисперсией воспроизводимости соотношением (15.12):

, (15.12)

где – число повторений опытов.

Таблица 15.2

Данные для построения матриц ротатабельного планирования второго порядка

Число факторов к	Число точек			Величина плеча звёздных точек L	Общее число опытов N	Примечания (о ядре плана)
	«ядра» nя	звёздных nl	Нулевых n0
2	4	4	5	1.414	13	ПФЭ
3	8	6	6	1.682	20	ПФЭ
4	16	8	7	2.000	31	ПФЭ
5	32	10	10	2.378	52	ПФЭ
5	16	10	6	2.000	32	Полуреплика
6	64	12	15	2.828	91	ПФЭ
6	32	12	9	2.378	53	Полуреплика
7	128	14	21	3.333	163	ПФЭ
7	64	14	14	2.828	92	Полуреплика

Таблица 15.3

Матрица планирования ротатабельного плана второго порядка для к = 2

№ опыта	Точки	X1	X2
1 2 3 4	«ядра»	+ - + -	+ + - -
5 6 7 8	«звёздные»	-1.414 +1.414 0 0	0 0 -1.414 +1.414
9 10 11 12 13	нулевые	0 0 0 0 0	0 0 0 0 0

Таблица 15.4

Матрица планирования ротатабельного плана второго порядка для к = 3

№ опыта	Точки	X1	X2	X3
1 2 3 4 5 6 7 8	«ядра»	+ - + - + - + -	+ + - - + + - -	+ + + + - - - -
9 10 11 12 13 14	«звёздные»	-1.68 +1.68 0 0 0 0	0 0 -1.68 +1.68 0 0	0 0 0 0 -1.68 +1.68
15 16 17 18 19 20	«нулевые»	0 0 0 0 0 0	0 0 0 0 0 0	0 0 0 0 0 0

Таблица 15.5

Значения коэффициентов, неиспользуемых для расчёта коэффициентов регрессии при ротатабельном планировании второго порядка

Число факторов (К)	Число опытов (N)	Коэффициенты
		а1	а2	а3	а4	а5	А6	а7
2	13	0.2000	0.1000	0.1250	0.2500	0.1250	0.0187	0.1000
3	20	0.1663	0.0568	0.0732	0.1250	0.0625	0.0069	0.0568
4	31	0.1428	0.0357	0.0417	0.0625	0.0312	0.0036	0.0357
5*	32	0.1591	0.0341	0.0417	0.0625	0.0312	0.0028	0.0341
5	52	0.0988	0.0191	0.0231	0.0312	0.0156	0.0015	0.0191
6*	53	0.1108	0.0187	0.0231	0.0312	0.0156	0.0012	0.0187
6	91	0.0625	0.0098	0.0125	0.0156	0.0078	0.0005	0.0098
7*	92	0.0730	0.098	0.0125	0.0156	0.0078	0.0005	0.0098
7	163	0.0398	0.0052	0.0066	0.0078	0.0039	0.0002	0.0052

* - полуреплика.

Таблица 15.6

Значения коэффициентов, используемых для оценки значимости коэффициентов регрессии в ротатабельных планах

при к = 25

Число факторов (к)	Число опытов плана(N)	Коэффициенты
		а8	а9	а10	а11
2 3 4 5	13 20 31 52	0.2000 0.1663 0.1428 0.1591	0.125 0.0732 0.0417 0.0417	0.1438 0.0694 0.0341 0.0341	0.2500 0.1250 0.0625 0.0625

Дисперсия воспроизводимости находится по уравнению:

. (15.13)

Дисперсию адекватности модели при равномерном дублировании всех опытов плана находят по формуле:

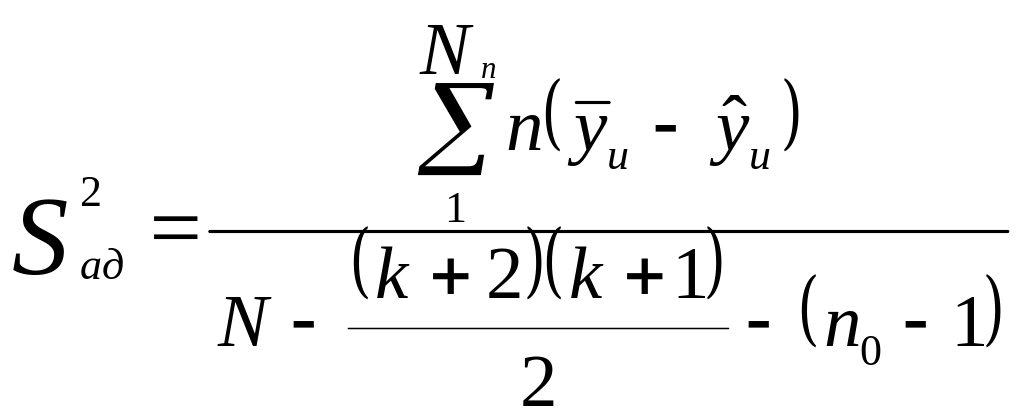, (15.14)

где –общее число опытов плана, включая и параллельные опыты в нулевой точке; – число опытов плана, имеющих одинаковое число повторений; – значение параметра оптимизации, вычисленное по модели, для условий n-го опыта.

Если опыты дублируются только в нулевой точке, то уравнение (15.15) принимает иной вид:

, (15.15)

где – остаточная сумма квадратов; – сумма квадратов отклонений; – число степеней свободы;  - число коэффициентов уравнения; – число повторений нулевого опыта.

Далее определяется расчётное значение критерия Фишера (13.25).

Особенности ротатабельного планирования второго порядка рассмотрим на конкретном примере при изучении зависимости критерия оптимизации ( ) от двух факторов (к = 2). в этом случае применяем матрицу планирования, показанную в табл. 15.3.

Из табл. 15.2 следует, что число опытов в матрице равно 13 (N=13), в том числе четыре повторных опыта в нулевой точке (n_я=4).

При кодировании факторов учитывали их интервалы и уровни варьирования, приведённые в табл. 15.7.

Таблица 15.7

Уровни и интервалы варьирования факторов

Факторы	Уровни варьирования					Интервалы варьирования(Е)
	-1.414	-1	0	+1	+1.414
С – концентрация реагента, %(X1)	1.2	1.4	1.9	2.4	2.6	0.5
t – температура, 0С(X2)	28	40	70	100	112	30

Значения факторов в «звёздных» точках были найдены с помощью соотношения, характеризующего связь натуральных и кодированных величин:

, (15.16)

где – кодированное значение фактора; и – натуральные значения фактора (соответственно его текущее значение и значение на нулевом уровне); – натуральное значение интервала варьирования.

В нашем случае:

В результате была построена рабочая матрица, реализация которой позволила установить экспериментальные значения параметра оптимизации (табл. 15.8).

Таблица 15.8

Матрица планирования, рабочая матрица и результаты эксперимента

№ опыта	Матрица планирования		Рабочая матрица			Данные к примеру
	X1	X2	C1,%	t,0C	yu	Yu	(yu-yu)2
1	+	+	2.4	100	50	49.9	0.01
2	-	+	1.4	100	67	65.2	3.24
3	+	-	2.4	40	60	62.4	5.76
4	-	-	1.4	40	70	70.6	0.36
5	-1.414	0	1.2	70	70	68.1	3.61
6	+1.414	0	2.6	70	50	51.5	2.25
7	0	-1.414	1.9	28	72	70.6	1.96
8	0	+1.414	1.9	112	56	57.6	2.25
9	0	0	1.9	70	62	64.0	4.00
10	0	0	1.9	70	64	64.0	0.00
11	0	0	1.9	70	68	64.0	16.00
12	0	0	1.9	70	64	64.0	0.00
13	0	0	1.9	70	62	64.0	4.00

По результатам эксперимента находим значения коэффициентов регрессии следующего уравнения:

. (15.17)

Для определения этих коэффициентов используем уравнения (15.4 – 15.7) и данные табл.15.5.

b₁ = -5.875, b₂ = -4.500, b₁₂=-1.750, b₁₁ = -2.112, b₂₂ = 0.112.

Таким образом, уравнение (15.17) принимает вид:

. (15.18)

Проверим гипотезу об адекватности уравнения:

,

,

.

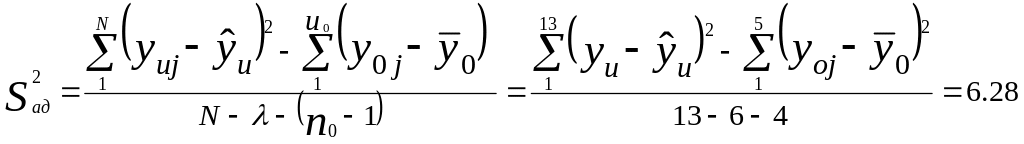Зная число степеней свободы, определяем табличное значение критерия Фишера для 95%-ной доверительной вероятности

F_табл.=6.85.

Сравнение табличного и расчётного значений критерия Фишера (F_таблF_расч) показывает, что полученное уравнение регрессии можно считать адекватным с доверительной вероятностью 0.95.

Значимость коэффициентов регрессии проверяем с учётом уравнений (15.8 – 15.12) и данных табл. 15.6:

; ;

; ;

; ;

; ;

; .

Сравнение абсолютных коэффициентов регрессии и соответствующих погрешностей в их оценке показывает, что с доверительной вероятностью 0.95 в уравнении (15.18) можно считать значимыми все коэффициенты, кроме b₁₂ и b₂₂. В результате этого уравнение принимает вид:

.