Задача 5. Часові ряди

Є умовні дані про обсяги споживання електроенергії (y_t) жителями регіону за 16 кварталів (№ варіанта).

Потрібно:

1. Побудувати автокореляційну функцію і зробити висновок про наявність сезонних коливань.

2. Побудувати адитивну і мультиплікативну моделі часового ряду.

3. Зробити прогноз на 2 квартали вперед.

Розв’язування.

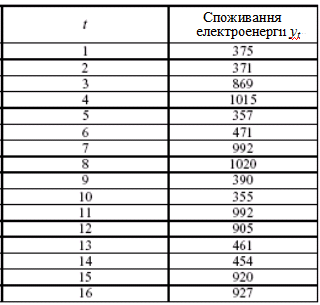
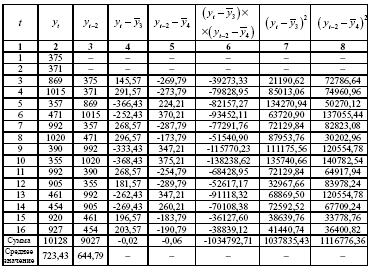
1. Нехай є деякі умовні дані про обсяги споживання електроенергії жителями регіону (табл. 5.1).

Таблиця 5.1.

Побудуємо поле автокореляції (рис.5.1).

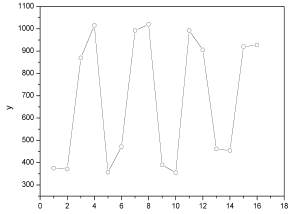
Рис. 5.1.

З графіка видно, що значення у утворюють пилкоподібну фігуру. Розрахуємо декілька послідовних коефіцієнтів автокореляції. Для цього складемо першу додаткову таблицю (табл. 5.2).

Таблиця 5.2.

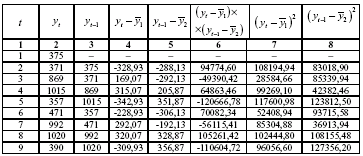
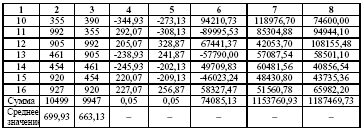
Варто зауважити, що середні значення одержуються шляхом ділення не на 16, а на 15, оскільки тепер на одно спостереження менше.

Обчислюємо коефіцієнт автокореляції першого порядку:

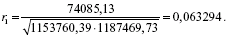
Складемо додаткову таблицю для розрахунку коефіцієнта автокореляції другого порядку (табл. 5.3).

Таблиця 5.3.

Отже,

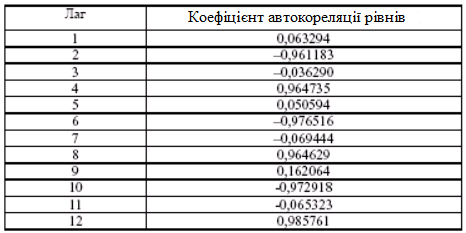
Аналогічно знаходяться коефіцієнти автокореляції більш високих порядків, а всі одержані значення заносимо у зведену таблицю (табл. 5.4).

Таблиця 5.4.

Корелограма (рис. 5.2).

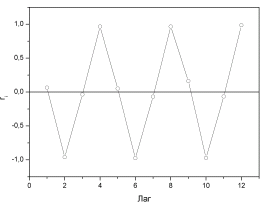
Рис. 5.2.

Аналіз корелограми і графіка початкових рівнів часового ряду дозволяє зробити висновок про наявність у часовому ряді, який вивчається, сезонних коливань з періодом у 4 квартали.

2. Розрахуємо компоненти адитивної моделі заданого часового ряду.

Крок 1. Проведемо вирівнювання початкових рівнів ряду методом ковзної середньої. Для цього:

2.1. Сумуємо рівні ряду послідовно за кожні чотири квартали зі зсувом на один момент часу і визначимо умовні річні обсяги споживання електроенергії (колонка 3 таблиці 5.5).

2.2. Розділимо одержані суми на 4, знайдемо ковзні середні (колонка 4 таблиці 5.5). Одержані таким чином вирівняні значення не містять сезонної компоненти.

2.3. Приведемо ці значення у відповідність з фактичними моментами часу, для чого знайдемо середні значення із двох послідовних ковзних середніх – центровані ковзні середні (колонка 5 таблиці 5.5).

Таблиця 5.5.

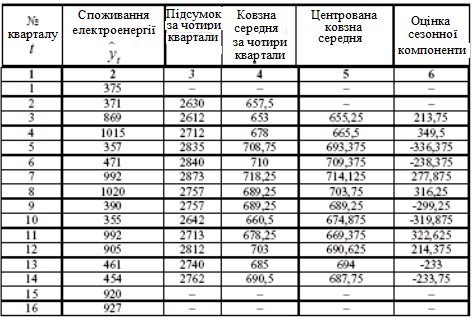
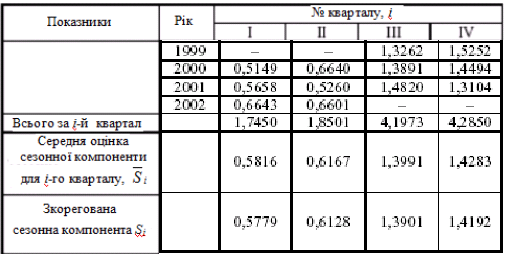
Крок 2. Знайдемо оцінки сезонної компоненти як різницю між фактичними рівнями ряду і центрованими ковзними середніми (колонка 6 таблиці 5.5). Використовуємо ці оцінки для розрахунку значень сезонної компоненти S_i (таблиця 5.6). Для цього знайдемо середні за кожний квартал (для всіх років) оцінки сезонної компоненти S_i.

Таблиця 5.6.

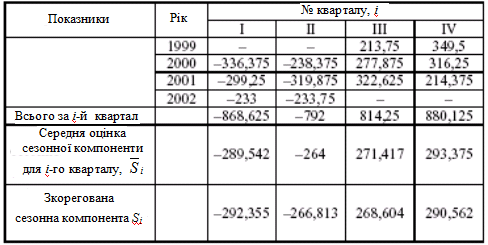
В моделях із сезонною компонентою, як правило, вважають, що сезонні впливи за період взаємогасяться. В адитивній моделі це виражається в тому, що сума значень сезонної компоненти для всіх кварталів повинна дорівнювати нулю.

Для даної моделі маємо:

Коригуючий множник:

Розрахуємо кореговані значення сезонної компоненти (S_i= -k) і заносимо одержані дані в таблицю 5.6.

Перевіримо рівність нулю суми значень сезонної компоненти:

Крок 3. Виключимо вплив сезонної компоненти, обчислюючи її значення для кожного рівня початкового часового ряду. Одержимо величини Т+Е=Y-S (колонка 4 таблиці 5.7). Ці значення розраховуються для кожного періоду часу і містять тільки тенденцію і випадкову компоненту.

Таблиця 5.7.

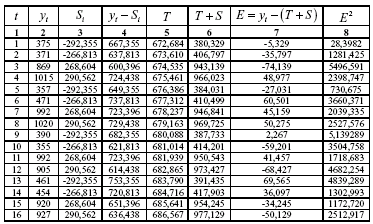
Крок 4. Визначимо компоненту Т даної моделі. Для цього проведемо аналітичне вирівнювання ряду (Т+Е) за допомогою лінійного тренду. Результати аналітичного вирівнювання такі:

Підставивши в це рівняння значення t=1, 2, …, 16, знайдемо рівні для кожного моменту часу (колонка 5 таблиці 5.7).

Крок 5. Знайдемо значення рівнів ряду, одержані з адитивної моделі. Для цього додамо до рівнів Т значення сезонної компоненти для відповідних кварталів (колонка 6 таблиці 5.7).

На одному графіку відкладемо фактичні значення рівнів часового ряду і теоретичні, одержані з адитивної моделі (рис. 5.3).

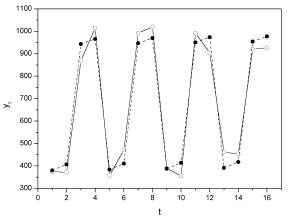
Рис. 5.3.

Для оцінки якості побудованої моделі застосуємо суму квадратів одержаних абсолютних похибок:

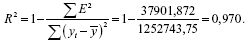
Отже, можна сказати, що адитивна модель пояснює 97% загальної варіації рівнів часового ряду по кварталах за 4 роки.

Крок 6. Прогнозування за адитивною моделлю. Вважаємо, що у нашому прикладі необхідно дати прогноз про споживання електроенергії на 1-й і 2-й квартали 2003 року. Прогнозне значення F_t рівня часового ряду в адитивній моделі є сумою трендової і сезонної компонент. Для визначення трендової компоненти скористаємося рівнянням тренду:

Одержимо:

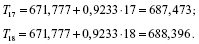
Значення сезонних компонент за відповідні квартали дорівнюють:

Таким чином,

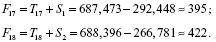
Тобто за перші два квартали 2003 р. варто очікувати порядку 395 і 422 обсяги споживання електроенергії відповідно.

Побудуємо тепер мультиплікативну модель.

Крок 1. Методика, яка використовується на цьому кроці співпадає з методикою побудови адитивної моделі (табл. 5.8).

Таблиця 5.8.

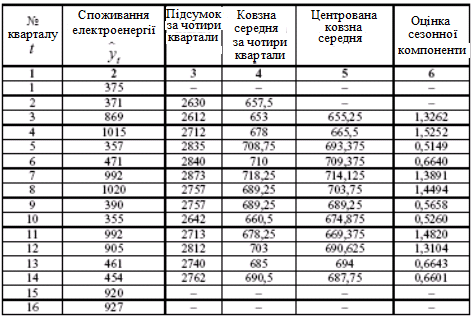
Крок 2. Знайдемо оцінки сезонної компоненти як частки від ділення фактичних рівнів ряду на центровані ковзні середні (колонка 6 таблиці 5.8). Ці оцінки використовуються для розрахунку сезонної компоненти S (табл. 5.9). Для цього знайдемо середні за кожний квартал оцінки сезонної компоненти S_t. Так як і в адитивній моделі вважається, що сезонні впливи за період взаємопогашаються. В мультиплікативній моделі це виражається в тому, що сума значень сезонної компоненти для всіх кварталів повинна дорівнювати числу періодів у циклі. В нашому випадку число періодів одного циклу дорівнює 4.

Таблиця 5.9.

Маємо:

Визначаємо коригуючий коефіцієнт:

Скориговані значення сезонної компоненти S_t одержуються при множенні її середньої оцінки на коригуючий множник k.

Перевіряємо рівність 4 суми значень сезонної компоненти:

Крок 3. Розділимо кожний рівень початкового ряду на відповідне значення сезонної компоненти. В результаті одержуємо величини (колонка 4 таблиці 5.10), які містять тільки тенденцію і випадкову компоненту.

Таблиця 5.10.

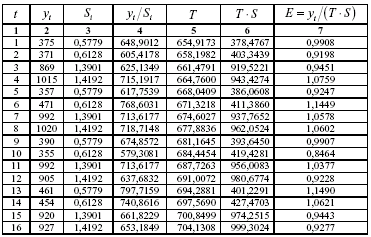
Крок 4. Визначимо компоненту Т в мутиплікативній моделі. Для цього розрахуємо параметри лінійного тренду, використовуючи рівні ТЕ. В результаті одержимо рівняння тренду:

Підставивши в це рівняння значення t=1, 2, ..., 16, знайдемо рівні Т для кожного моменту часу (колонка 5 таблиці 5.10).

Крок 5. Знайдемо рівні ряду, помноживши значення Т на відповідні значення сезонної компоненти (колонка 6 таблиці 5.10). На одному графіку відкладемо фактичні значення рівнів часового ряду і теоретичні, одержані за мультиплікативною моделлю (рис. 5.4).

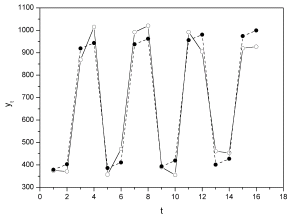
Рис. 5.4.

Розрахунок похибки в мультиплікативній моделі проводиться за формулою:

Для порівняння мультиплікативної моделі з іншими моделями часового ряду можна за аналогією з адитивною моделлю використати суму квадратів абсолютних похибок :

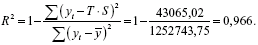
Порівнюючи показники детермінації адитивної і мультиплікативної моделей, робимо висновок, що вони наближено однаково апроксимують початкові дані.

Крок 6. Прогнозування за мультиплікативною моделлю. Якщо вважати, що для нашого прикладу необхідно дати прогноз про споживання електроенергії на 1 і 2 квартали 2003 р., прогнозне значення F_t рівня часового ряду в мультиплікативній моделі є добуток трендової і сезонної компонент. Для визначення трендової компоненти користуємось рівняння тренду:

Одержуємо:

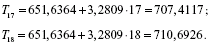
Значення сезонних компонент за відповідні квартали дорівнюють:

Таким чином:

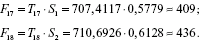
Отже, в перші 2 квартали 2003 р. варто очікувати споживання електроенергії в 409 і 436 одиниць відповідно.

Робимо загальний висновок: адитивна і мультиплікативна моделі дають приблизно однаковий результат із прогнозу.

Перевіримо тепер гіпотезу про наявність автокореляції в залишках для адитивної моделі нашого часового ряду. Початкові дані і проміжні результати розрахунку заносимо в табл. 5.11.

Таблиця 5.11.

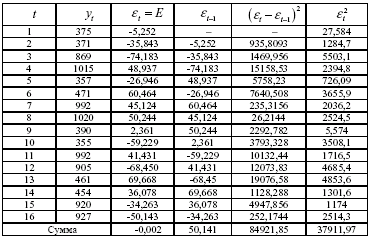
Фактичні значення критерію Дарбіна-Уотсона для даної моделі складають:

Сформулюємо гіпотези: Н₀ – в залишках немає автокореляції; Н₁ – в залишках є додатна автокореляція; Н₁^* - в залишках є від’ємна автокореляція. Задамо рівень значимості =0,05. В таблиці значень критерію Дарбіна-Уотсона знаходимо для числа незалежних параметрів моделі к=1 (розглядаємо тільки залежність від часу t) критичні значення d_L=1,10, d_U=1,37. Фактичне значення d-критерію Дарбіна-Уотсона потрапляє в інтервал

Отже, немає підстав відхиляти гіпотезу Н₀ про відсутність автокореляції в залишках.