Задача 3. Множинна регресія і кореляція

На 20 підприємствах регіону вивчається залежність вироблення продукції на одного працівника у (тис. грн.) від введення в дію нових основних фондів х₁ (% від вартості фондів на кінець року) і від питомої ваги робочих високих кваліфікацій в загальній чисельності працюючих х₂ (%) (табл. 3.1).

Таблиця 3.1.

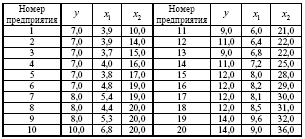
Потрібно:

1. Побудувати лінійну модель множинної регресії. Записати стандартизоване рівняння множинної регресії. На основі стандартизованих коефіцієнтів і середніх коефіцієнтів еластичності ранжувати фактори за мірою їх впливу на результат.

2. Знайти коефіцієнти парної, окремої і множинної кореляції. Проаналізувати їх.

3. Знайти скорегований коефіцієнт множинної детермінації. Порівняти його із не скорегованим (загальним) коефіцієнтом детермінації.

4. За допомогою F-критерію Фішера оцінити статистичну надійність рівняння регресії і коефіцієнта детермінації .

5. За допомогою окремих F-критеріїв Фішера оцінити доцільність включення в рівняння множинної регресії фактора х₁ після х₂ і фактора х₂ після х₁.

6. Скласти рівняння лінійної парної регресії, залишивши лише один значимий фактор.

Розв’язування.

Для зручності проведення розрахунків помістимо результати проміжних розрахунків у таблицю (табл. 3.2).

Таблиця 3.2.

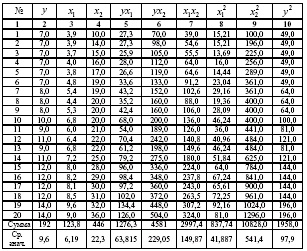
Знайдемо середні квадратичні відхилення ознак:

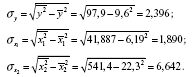
1. Обчислимо параметри лінійного рівняння множинної регресії.

Для знаходження параметрів лінійного рівняння множинної регресії

необхідно розв’язати систему лінійних рівнянь відносно невідомих параметрів a, b₁, b₂:

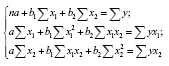
або скористатися формулами:

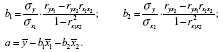
Знайдемо спочатку парні коефіцієнти кореляції:

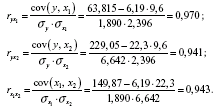
а потім відповідні параметри:

Таким чином, одержали таке рівняння множинної регресії:

Рівняння регресії показує, що при збільшенні введення в дію основних фондів на 1% (при незмінному рівні питомої ваги робочих високої кваліфікації) вироблення продукції на одного робочого збільшиться в середньому на 0,946 тис. грн., а при збільшенні питомої ваги робочих високої кваліфікації в загальній чисельності робочих на 1% (при незмінному рівні введення в дію нових основних фондів) вироблення продукції на одного робочого збільшиться в середньому на 0,086 тис. грн.

Коефіцієнти ₁ і ₂ стандартизованого рівняння регресії

знаходяться по формулам:

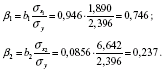
Таким чином, маємо рівняння

Оскільки стандартизовані коефіцієнти регресії можна порівнювати між собою, то можна сказати, що введення в дію нових основних фондів більше впливає на вироблення продукції, чим питома вага робочих високої кваліфікації.

Порівнювати вплив факторів на результат можна також за допомогою середніх коефіцієнтів еластичності:

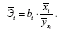
Обчислюємо:

Таким чином, Збільшення тільки основних фондів (від свого середнього значення) або тільки питомої ваги робочих високої кваліфікації на 1% збільшує в середньому вироблення продукції на 0,61% або на 0,20% відповідно. Отже, підтверджується більший вплив на результат у фактора х₁, чим фактора х₂.

2. Коефіцієнти парної кореляції уже знайдені:

Вони вказують на досить сильний зв’язок кожного фактора з результатом, а також високу міжфакторну залежність (фактори х₁ і х₂ явно колінеарні, оскільки =0,943>0,7). При такій сильній міжфакторній залежності рекомендується один із факторів виключити із розгляду.

Окремі коефіцієнти кореляції характеризують тісноту зв’язку між результатом і відповідним фактором при елімінуванні (усуненні впливу) інших факторів, включених в рівняння регресії.

При двох факторах окремі коефіцієнти кореляції розраховуються таким чином:

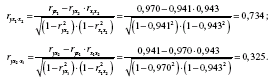
Якщо порівняти коефіцієнти парної і окремої кореляції, то можна бачити, що із-за високої міжфакторної залежності коефіцієнти парної кореляції дають завищені оцінки тісноти зв’язку. Саме з цієї причини рекомендується при наявності сильної колінеарності (взаємозв’язку) факторів виключити із дослідження той фактор, у якого тіснота парної залежності менша, чим тіснота міжфакторного зв’язку.

Коефіцієнт множинної кореляції визначається через матрицю парних коефіцієнтів кореляції:

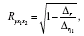
де

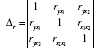
- визначник матриці попарних коефіцієнтів кореляції;

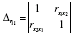
- визначник матриці міжфакторної кореляції.

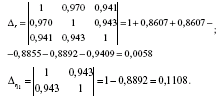
Коефіцієнт множинної кореляції:

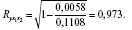
Аналогічний результат одержимо при використанні інших формул:

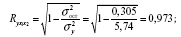
Коефіцієнт множинної регресії показує на досить сильний зв’язок між набором факторів і результатом.

3. Не скоригований коефіцієнт множинної детермінації =0,947 оцінює долю варіації результату за рахунок поданих у рівнянні факторів у загальній варіації результату. Тут ця доля складає 94,7% і вказує на досить високу міру обумовленості варіації результату варіацією факторів, іншими словами – на досить тісний зв’язок факторів із результатом.

Скорегований коефіцієнт множинної детермінації

визначає тісноту зв’язку з урахуванням степенів свободи загальної і залишкової дисперсій. Він дає таку оцінку тісноти зв’язку, яка не залежить від числа факторів і тому може порівнюватися для різних моделей із різним числом факторів. Обидва коефіцієнти вказують на досить високу (більше 94%) детермінованість результату у в моделі із факторами х₁ і х₂.

4. Оцінку надійності рівняння регресії в цілому і показника тісноти зв’язку дає F-критерій Фішера:

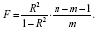
В нашому випадку фактичне значення F-критерію Фішера:

Одержали, що

тобто ймовірність випадково одержати таке значення F-критерію не перевищує допустимий рівень значимості 5%. Отже, одержане значення не випадкове, воно сформувалось під впливом істотних факторів, тобто підтверджується статистична значимість всього рівняння і показника тісноти зв’язку .

5. За допомогою F-критерію Фішера оцінимо доцільність включення в рівняння множинної регресії фактора х₁ після х₂ і фактора х₂ після х₁ за допомогою формул:

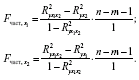
Одержали, що

Отже, включення в модель фактора х₂ після того, як в модель включений фактор х₁ статистично недоцільно: приріст факторної дисперсії за рахунок додаткової ознаки х₂ виявляється незначним, неістотним; фактор х₂ включати в рівняння після фактора х₁ не варто.

Якщо змінити початковий порядок включення факторів у модель і розглянути варіант включення х₁ після х₂, то результат розрахунку окремого F-критерію для х₁ буде іншим,

тобто ймовірність його випадкового формування менша прийнятого стандарту =0,05 (5%). Отже, значення окремого F-критерію для додаткового включення фактора х₁ не випадкове, є статистично значимим, надійним, достовірним: приріст факторної дисперсії за рахунок додаткового фактора х₁ є істотним. Фактор х₁ повинен бути присутнім у рівнянні, в тому числі і в варіанті, коли він додатково включається після фактора х₂.

6. Загальний висновок полягає в тому, що множинна модель із факторами х₁ і х₂ із =0,947 містить неінформативний фактор х₂. Якщо виключити фактор х₂, то можна обмежитися рівнянням парної регресії: