8. Нормальний розподіл. Кажуть, що неперервна випадкова величина розподілена нормально, якщо її щільність розподілу має вигляд

(19)

для будь-якого і довільних чисел і .

Графік функції називають нормальною кривою або кривою Гауса. Ця крива є симетричною відносно прямої і має одну точку максимуму при :

(20)

величина якого залежить від параметра .

При та нормальну криву називають нормованою.

Зауваження. Якщо випадкова величина розподілена за нормальним законом з параметрами і , то випадкова величина буде розподілена за нормованим нормальним законом.

Функція розподілу нормально розподіленої випадкової величини з параметрами і має вигляд

, (21)

де 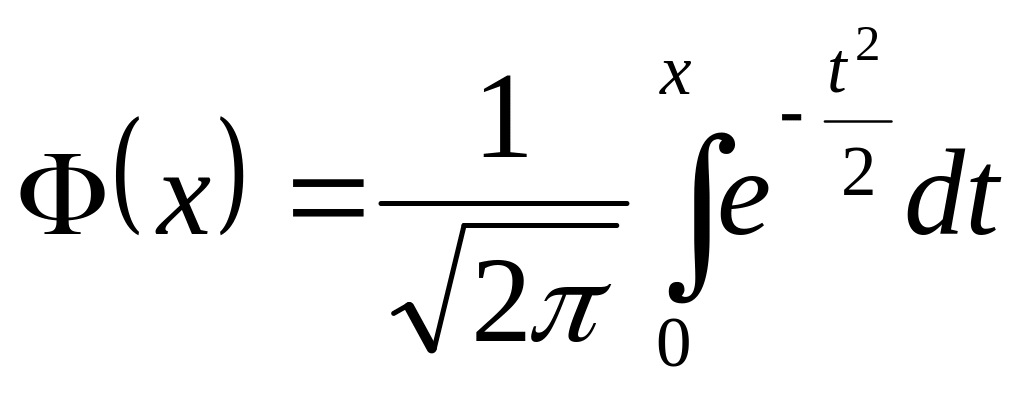– функція Лапласа. Часом замість використовують функцію Тоді

Використовуючи формулу (20), легко знайти ймовірність попадання випадкової величини, розподіленої за нормальним законом, в інтервал

(22)

На підставі цієї ж формули одержимо формулу для знаходження ймовірності відхилення нормально розподіленої випадкової величини від свого математичного сподівання на наперед задану величину

. (23)

Якщо у формулі (22) покласти , то

З останньої рівності виходить такий висновок: ймовірність того, що нормально розподілена випадкова величина набуває своїх значень у проміжку , дорівнює 0, 9973. Це означає, що – практично достовірна подія. Одержане твердження називають правилом “трьох сигм”.

Для випадкової величини , яка має нормальний розподіл з параметрами і ,

(24)

9. Логарифмічно нормальний розподіл. Неперервна невід’ємна випадкова величина має логарифмічно нормальний (логнормальний) розподіл, якщо величина має нормальний розподіл.

На підставі визначення випадкової величини , де – нормально розподілена випадкова величина з параметрами і , можна знайти щільність розподілу першої з цих величин:

(25)

10. Розподіл Вейбула. Неперервна випадкова величина , яка набуває невід’ємних значень, має розподіл Вейбула з параметрами і , якщо щільність її розподілу має вигляд

(26)

Розглянутий раніше показниковий розподіл з параметром є частковим випадком розподілу Вейбула при

11. Гамма-розподіл. Випадкова величина має гамма-розподіл з параметрами і , якщо щільність її розподілу має вигляд

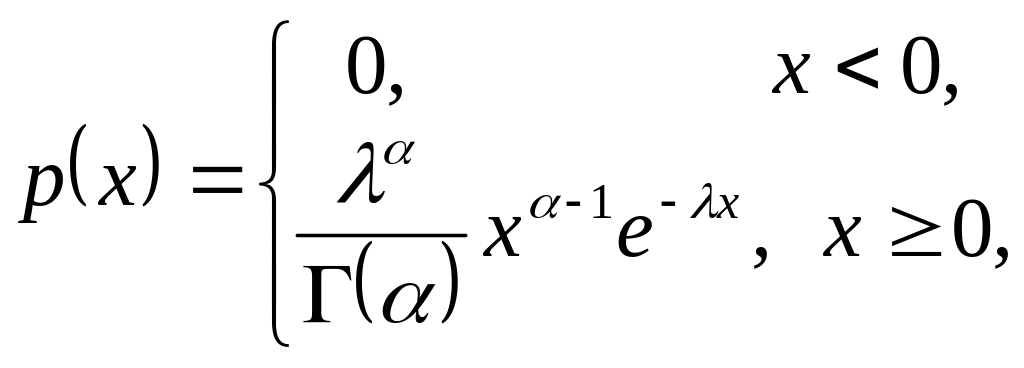(27)

де – гамма-функція Ейлера.

Розглянутий раніше показниковий розподіл з параметром є частковим випадком гамма-розподілу при

Для гамма-розподілу

(28)

Якщо , то отримаємо розподіл з ступенями вільності.

На практиці часто зустрічаються закони розподілу випадкових величин, які є функціями незалежних нормальних випадкових величин. Розглянемо три з них, які найчастіше зустрічаються при моделюванні випадкових явищ.

12. Розподіл “хі-квадрат” ( -розподіл). Нехай – нормальні, нормовані незалежні випадкові величини, тобто кожна з них розподілена за нормальним законом, має математичне сподівання рівне нулю і середнє квадратичне відхилення – рівне одиниці. Тоді випадкова величина

(29)

має розподіл “хі-квадрат” ( -розподіл) з ступенями вільності.

Щільність розподілу цієї випадкової величини є такою

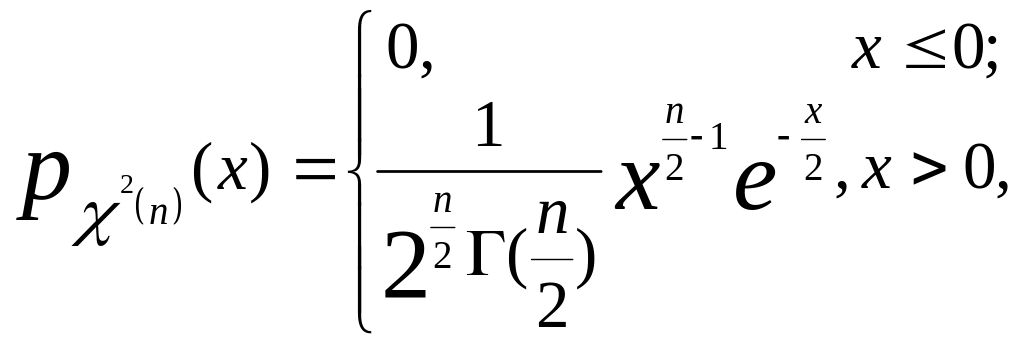(30)

де – гамма-функція Ейлера.

Для випадкової величини, яка має розподіл “хі-квадрат” з ступенями вільності числові характеристики є такими

(31)

Слід зауважити, що розподіл із зростанням числа ступенів вільності дуже повільно прямує до нормального розподілу. Тому цей розподіл при великих значеннях ( ) з достатньою для практичних розрахунків точністю можна апроксимувати (замінити) нормальним розподілом.

Розподіл табульований. У таблицях наведені -процентні точки розподілу (для ), які задовольняють співвідношення . Для значення , ураховуючи попередні міркування, визначають за допомогою таблиць нормального закону розподілу.

14. Розподіл Стьюдента ( -розподіл). Нехай – незалежні нормально розподілені випадкові величини, кожна з яких має математичне сподівання рівне нулю. Тоді випадкова величина

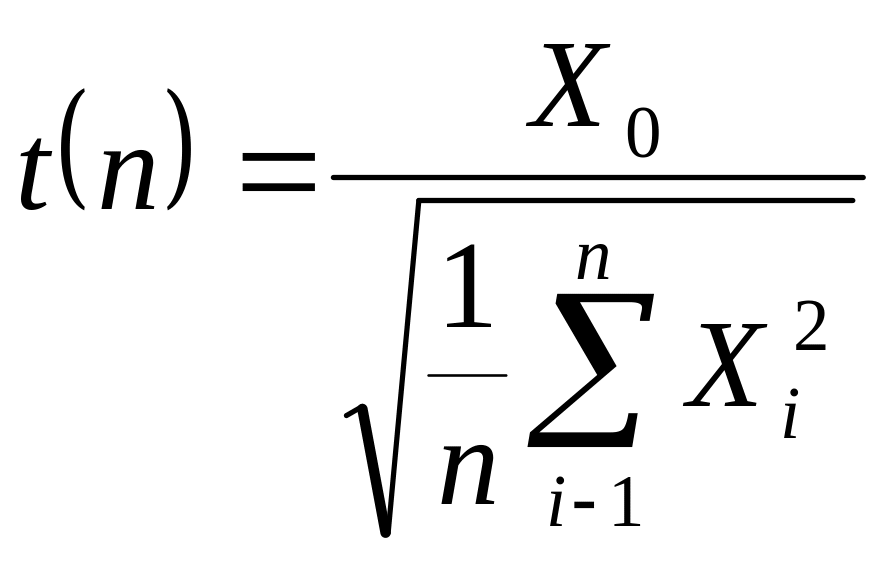(32)

має розподіл Стьюдента з ступенями вільності.

Цей розподіл не залежить від параметра . Для нього

(33)

Щільність розподілу випадкової величини, яка має -розподіл з ступенями вільності, обчислюється за формулою

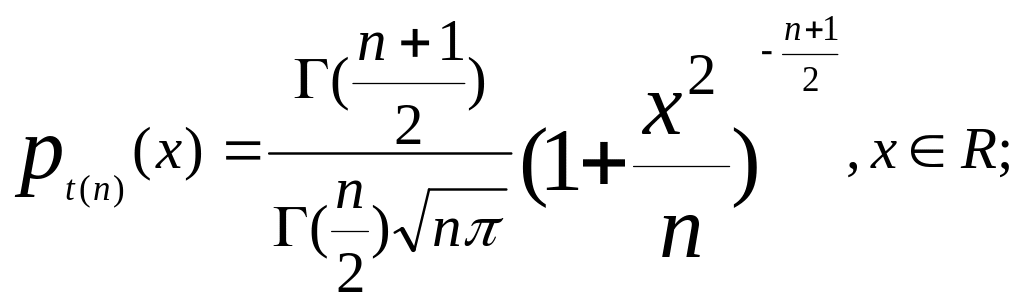(34)

де – гамма-функція Ейлера.

Графік щільності розподілу Стьюдента симетричний відносно осі ординат і за виглядом приблизно нагадує графік щільності нормального розподілу. Із зростанням числа ступенів вільності -розподіл наближуються до нормованого нормального розподілу.

15. Розподіл Фішера ( -розподіл). Нехай – незалежні нормально розподілені випадкові величини, кожна з яких має математичне сподівання рівне нулю. Тоді випадкова величина

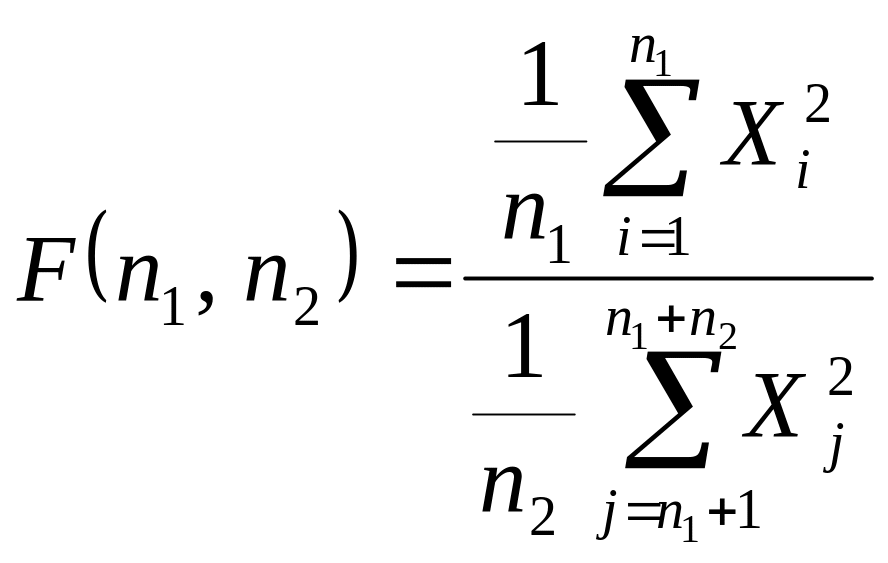(35)

має розподіл Фішера з та ступенями вільності.

Цей розподіл не залежить від параметра і має щільність

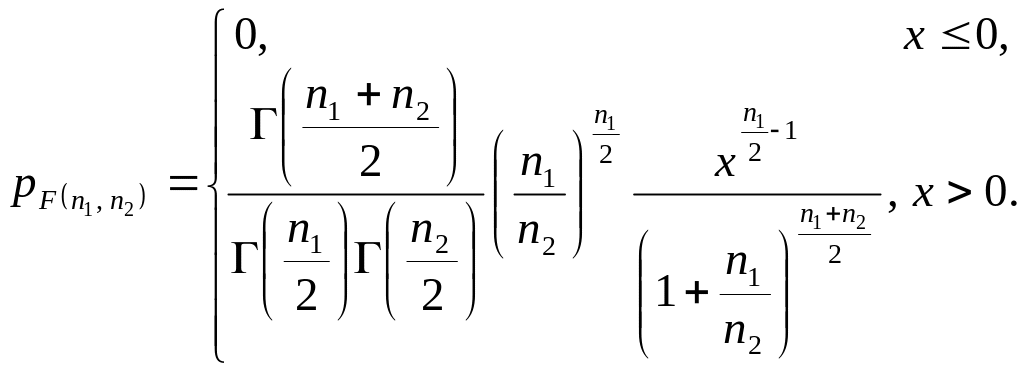(36)

Для математичне сподівання цього розподілу дорівнює

При великих та розподіл Фішера заміняють нормальним розподілом.