Одновимірні випадкові величини та їх числові характеристики

В попередніх розділах ми розглядали випадкові події. Крім випадкової події, одним з основних понять теорії ймовірностей є випадкова величина. Так, наприклад, при підкиданні грального кубика випадкові події, які полягають у випаданні на верхній його поверхні кількості очок 1, 2, 3, 4, 5 чи 6, можна інтерпретувати як можливі значення величини, яку далі ми будемо називати випадковою.

Випадковою величиною називають таку величину, яка в результаті випробування приймає лише одне числове значення, заздалегідь невідоме і обумовлене випадковими причинами.

Якщо, наприклад, ми підкидаємо дві монети, то в якості елементарних можна взяти такі події:  = ГГ = {на першій монеті випав “герб”, на другій – також “герб”};  = ГЦ = {на першій монеті випав “герб”, на другій – “цифра”};  = ЦГ = {на першій монеті випала “цифра”, на другій – “герб”};  = ЦЦ = {на першій монеті випала “цифра”, на другій – також “цифра”}. Звідси, кількість “гербів” , які випали, є функцією від елементарної події

(ГГ) = 2, (ГЦ) = 1, (ЦГ) = 1, (ЦЦ) = 0.

Оскільки результат випробування є випадковим, то значення є випадковим. Функція – випадкова величина, що визначена на множині елементарних подій Тобто, по іншому, випадковою величиною називають числову функцію , яка визначена на множині .

Випадкові величини бувають дискретними та неперервними.

Дискретною випадковою величиною називають таку величину, яка може приймати скінченну чи зліченну кількість значень з певними ймовірностями.

Наведені вище приклади були прикладами дискретних випадкових величин. Зокрема, в прикладі про підкидання двох монет, випадкова величина , що дорівнює кількості “гербів”, які випали, може приймати тільки три значення: нуль, один чи два. Оскільки елементарні події рівноможливі, то ймовірності кожної з них дорівнюють 1/4. Враховуючи несумісність подій та , можна стверджувати, що ймовірність того, що випадкова величина прийме своє значення нуль, або один чи два, відповідно дорівнює 1/4, 1/2 та 1/4. Звідси стає очевидним, що для задання випадкової величини крім її значень потрібно вказати ймовірності, з якими вони можуть появитися. Дискретну випадкову величину задає її закон розподілу.

Законом розподілу дискретної випадкової величини називають таке співвідношення, яке встановлює відповідність між кожним можливим значенням випадкової величини і його ймовірністю . Причому

Закон розподілу дискретної випадкової величини можна задати трьома способами: аналітичним, табличним і графічним. При першому з них окремо задаються можливі значення випадкової величини , а відповідні їм ймовірності розраховуються за наперед заданою функцією.

При табличному заданні закону розподілу можливі значення випадкової величини і їхні ймовірності задають у вигляді такої таблиці:

Таблиця 1

			…		…
			…		…

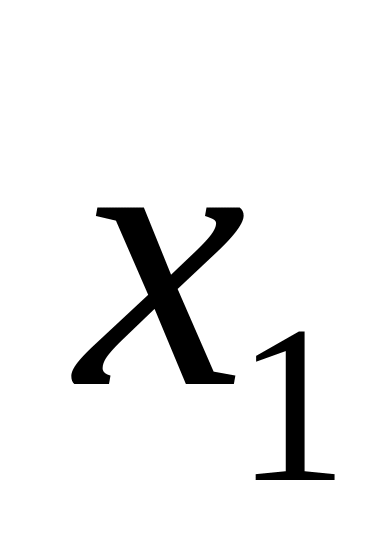
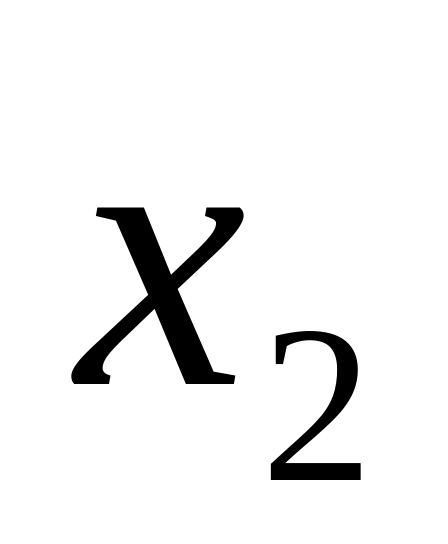
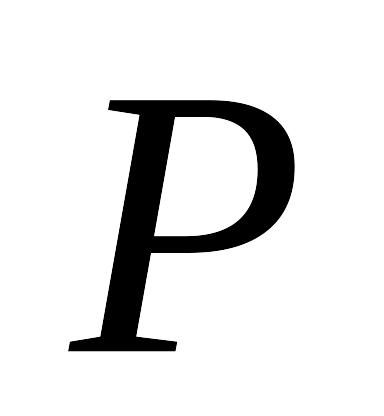
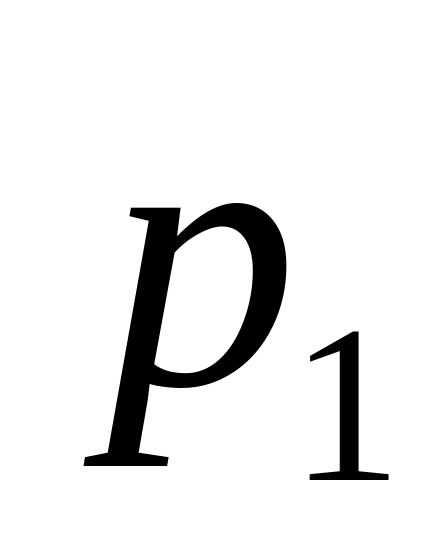
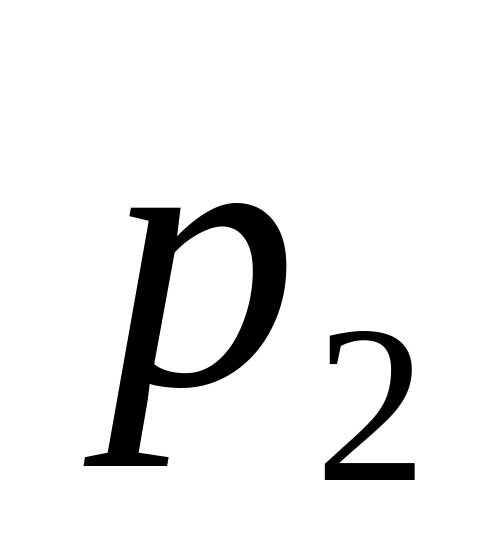
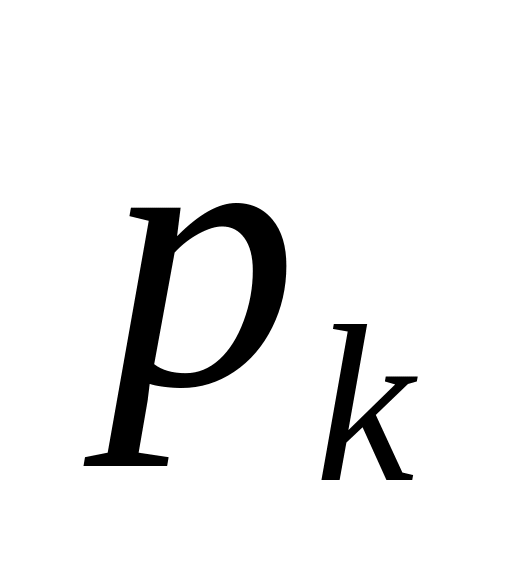
Сума ймовірностей, які записані у другому рядку цієї таблиці має дорівнювати одиниці. Таблицю 1 ще називають рядом розподілу випадкової величини.

Графічно задають закон розподілу дискретної випадкової величини таким чином: на координатній площині з прямокутною системою координат наносять точки , де відкладають на осі абсцис, а – на осі ординат. Якщо тепер з’єднати сусідні точки відрізками, то одержана ламана лінія називається многокутником розподілу випадкової величини.

Часто трапляються дискретні випадкові величини, що можуть приймати лише цілочислові значення. На особливу увагу заслуговують цілочислові випадкові величини, можливі значення яких є послідовні невід’ємні цілі числа 0, 1, 2, … . Такі величини досить часто описують реальні задачі. Залежно від того, за якою формулою будуть обчислюватися ймовірності , ці закони мають свою назву.

Для повнішої характеристики випадкової величини використовують функцію розподілу. Функція дійсної змінної , яка визначається ймовірністю того, що випадкова величина в результаті випробування прийме значення, менше за , тобто

(1)

називається функцією розподілу цієї випадкової величини. Якщо зрозуміло про яку випадкову величину йде мова, то індекс у позначенні функції розподілу опускають.

Цю функцію вводять як для дискретних, так і неперервних випадкових величин. На підставі формули (1), функцію розподілу дискретної випадкової величини визначають рівністю

(2)

де .

Функція розподілу має такі властивості:

1) значення функції розподілу належать проміжку , тобто

2) 

3) функція розподілу неспадна, тобто, якщо то

4) функція розподілу ненеперервна зліва, тобто,

5) ймовірність того, що випадкова величина набуде значення з напівінтервалу обчислюється за формулою

(3)

6) 

Поняття неперервної випадкової величини можна вводити по різному. Зокрема, випадкову величину називають неперервною (абсолютно), якщо існує невід’ємна функція така, що для всіх її функцію розподілу можна зобразити у вигляді

(4)

Будемо розглядати лише такі випадкові величини, для яких функція є неперервною, крім, можливо, скінченої кількості точок. Функцію називають щільністю розподілу. Графік функції називають кривою розподілу.