2.3. Змінний синусоїдний струм

2.3.1. Змінний струм у колі з активним опором

У колах постійного струму ми оперували омічним опором R, величина якого залежить від матеріалу, довжини і перерізу:

(2.15)

де ρ – питомий опір матеріалу (для міді ); l – довжина проводу, м; S – переріз проводу, мм².

У колах змінного струму в загальному випадку доводиться мати справу з 4-ма опорами: активним R, індуктивним , ємнісним , опором взаємоіндукції .

Розглянемо коло з активним опором R (рис. 2.8), яке підключене до джерела синусоїдної напруги:

(2.16)

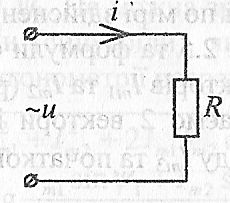
Рис 2.8

Як правило, не враховують вплив поверхневого ефекту і вважають, що активний опір R у колі змінного струму дорівнює омічному опору R у колі постійного струму.

Миттєве значення струму визначається за законом Ома:

(2. 17)

де — амплітуда струму.

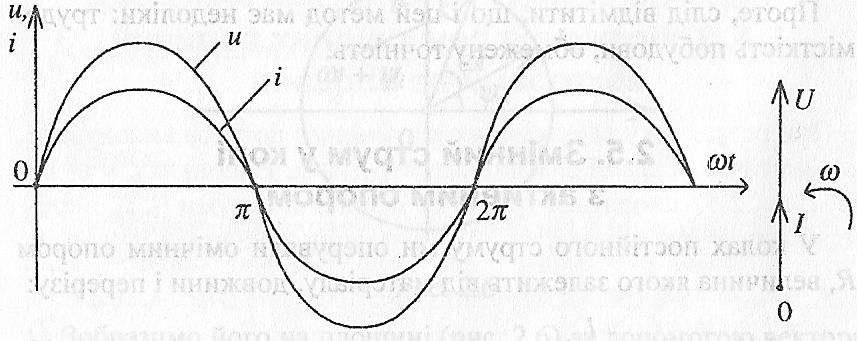
Рис. 2.9

У колі з активним опором R напруга і струм співпадають за фазою ( = 0), тобто вони синфазні і на рис. 2.9 показані їх хвильова і векторна діаграми.

Спад напруги на активному опорі також співпадає за фазою зі струмом

(2.18)

Електрична потужність у колі змінного струму з активним опором розраховується за тими формулами, що і в колі постійного струму:

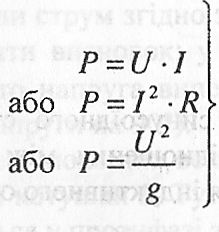(2.19)

Тут – провідність, розмірність потужності – Ват (Вт).

Активна потужність витрачається на перетворення електричної потужності в тепло, а також на перетворення в механічну потужність (обертання механізму, створення тягової сили електромагніту і т.п.).

2.3.2. Індуктивність у колі синусоїдного струму

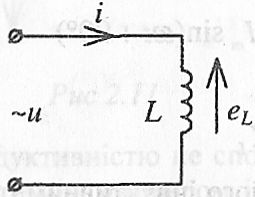
Рис 2.10

З курсу фізики відомо, що будь-яка котушка (обмотка) має індуктивність L та активний опір R. Розглянемо так звану ідеальну котушку, у якої R = 0; розмірність L – генрі.

Якщо котушкою протікає змінний синусоїдний струм

, (2 .20)

то в ній виникає EPC самоіндукції

(2.21)

Для того, щоб компенсувати цю EPC самоіндукції, необхідно прикласти напругу джерела, яка рівна по величині і протилежна за знаком:

(2.22)

Виконаємо диференціювання синусоїдного струму і при цьому встановимо фазові співвідношення між напругою і струмом, а також уведемо поняття індуктивного опору.

(2.23)

Відмітимо, що для взяття похідної, необхідно кутову частоту омега ввести під знак диференціювання, а щоб дріб не змінювався, ввести також і в чисельник. Візьмемо похідну:

(2. 24)

Замінимо косинусоїду на синусоїду, додавши до фазного

кута 90°:

(2.25)

Позначимо

(2.26)

і будемо називати його індуктивним опором.

Добуток ω·L має розмірність опору:

[ω·L] = 1/c·Гн = 1/c·Ом·с = Ом

Миттєве значення напруги:

(2.27)

Позначимо і тоді

(2.28)

Порівнявши струм згідно з (2.20) та напругу згідно з (2.28), можна зробити висновок: у колі з ідеальною індуктивністю , тобто напруга випереджає струм на 90° (або струм відстає від напруги на 90°).

На рис. 2.11 приведена векторна діаграма струму і напруги для ідеальної котушки L. Тут же показана EPC самоіндукції E, що знаходиться у протифазі з напругою джерела U.

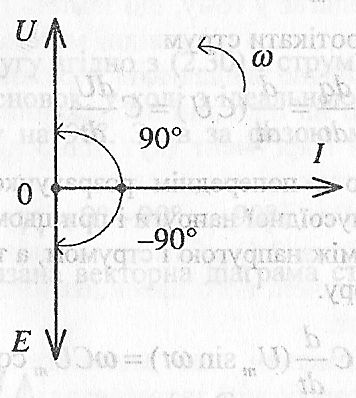
Рис 2.11

Коло з ідеальною індуктивністю не споживає із мережі активну потужність. Проте між джерелом і котушкою відбуваються урівноважені коливання з подвійною частотою активної енергії (R = 0). Електромагнітна енергія котушки створює магнітне поле, яке необхідне для роботи кіл з магнітопроводом (трансформаторів, електричних машин, електромагнітів і т.п.).