2.6.2. Резонанс струмів

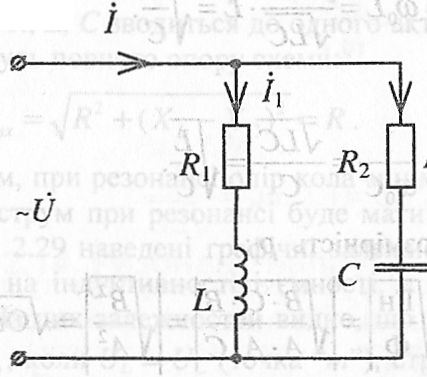
Щоб дослідити резонанс струмів необхідно мати котушку індуктивності і конденсатор, ввімкнути їх паралельно на джерело змінної напруги і виконати умови, за яких можливий резонанс (рис. 2.30).

І₂

Рис. 2.30

Ідеальним називають резонанс струмів, коли , тобто, коли індуктивність L і ємність C включені паралельно. У цьому випадку умова резонансу проста:

. (2.80)

Але у загальному випадку не можна нехтувати активними опорами R, особливо для вітки з котушкою індуктивності. Розглянемо цей більш загальний випадок.

При аналізі резонансу струмів доцільно скористатися провідностями віток, а також ввести поняття активних і реактивних складових струмів.

На рис. 2.30 перша вітка (R, L) має комплекс повного опору:

(2.81)

Комплекс повної провідності цієї вітки:

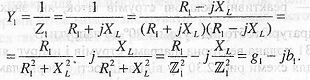(2.82)

Тут:

— активна провідність вітки,

— реактивна провідність вітки. Друга вітка (R, С) має комплекс повного опору:

(2.83)

Комплекс повної провідності цієї вітки:

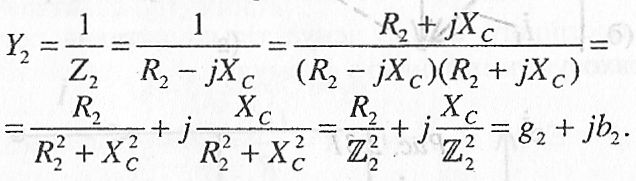(2.84)

Тут: – активна провідність вітки, – реактивна провідність вітки.

При виведенні аналітичного виразу для провідностей чисельник і знаменник перемножувалися на комплекс опору, спряжений знаменнику; ( та ).

Запишемо через провідності закон Ома для розрахунку комплексних значень струмів віток:

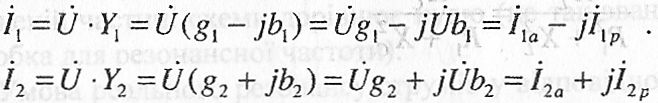. (2.85-86)

Тут: , – активні складові струмів віток, які співпадають за фазою з напругою ; , – реактивні складові струмів віток, які знаходяться в квадратурі, тобто під кутом до напруги .

На рис. 2.31 подана векторна діаграма струмів і напруг, яка побудована для схеми рис. 2.30 і у відповідності з формулами (2.85), (2.86).

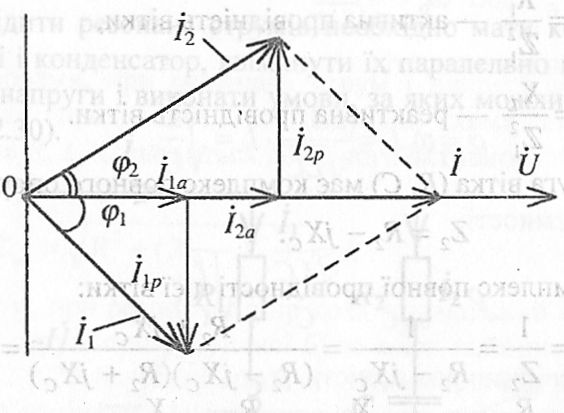
Рис. 2.31

При резонансі вектор напруги та струм в нерозгалуженій частині схеми повинні співпадати за фазою, тобто . Це можливо при умові, коли модулі реактивних провідностей віток рівні між собою, тобто

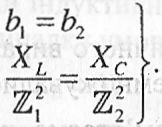(2.87)

В ідеальному випадку, коли , умова резонансу струмів, очевидно, зведеться до рівності . Це випливає з (2.87):

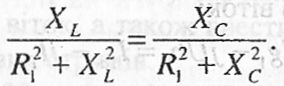
Звідки

, або . (2.88)

Тільки для ідеального резонансу струмів, коли активними опорами віток можна знехтувати, резонансна частота визначається так само, як і для резонансу напруг, тобто:

(2.89)

Струм при ідеальному резонансі струмів буде на 90° відставати від напруги , а струм на 90° випереджає напругу ; ці струми рівні за модулем і оскільки вони знаходяться в протифазі, то сумарний струм

.

На рис. 2.32 подані для ідеального резонансу струмів схема і векторна діаграма.

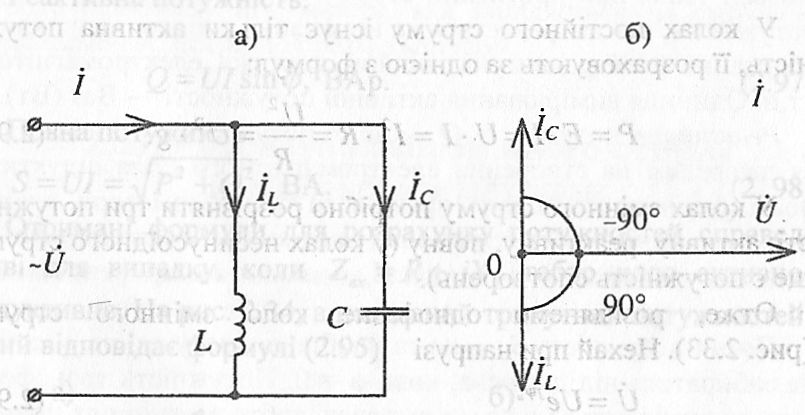
Рис. 2.32

При ідеальному резонансі струмів можна вести мову про те, що , бо в будь-який момент часу струм у нерозгалуженій частині схеми дорівнює нулю (це так званий фільтр- пробка для резонансної частоти).

Умова реального резонансу струмів у відповідності з (2.87) буде залежати не тільки від опорів x_L та x_C, але також і від активних опорів віток. Із допуском певної похибки розрахунків, коли можна не враховувати відносно малі значення активних опорів, будемо використовувати залежності, які правильні лише для ідеального резонансу струмів:

резонансна кутова частота: ;

резонансна частота: ;

характеристичний опір: .