2.5. Закони Ома та Кірхгофа у комплексній формі

Ці закони для кіл змінного струму відрізняються від кіл постійного струму тим, що все необхідно розглядати у комплексах: напруги, опори, струми.

Так, закон Ома у загальному вигляді формулюється так: комплекс діючого значення струму в колі прямо пропорційний комплексу діючого значення напруги і обернено пропорційний комплексу вхідного повного опору на затискачах джерела (рис. 2.19).

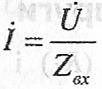(2.51)

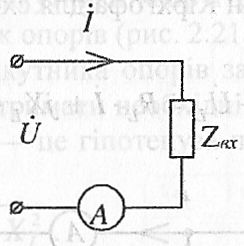
Рис. 2. 19

Закон Ома застосовується також у тих випадках, коли необхідно, наприклад, визначити струм у колі, тобто розрахувати модуль струму. В цьому випадку всі величини, які входять у формулу закону Ома, повинні бути подані в модулях:

(2.52)

Перший закон Кірхгофа відноситься до вузла і читається так: алгебраїчна сума комплексних діючих значень струмів, які сходяться у вузлі, дорівнює нулю.

(2.53)

Другий закон Кірхгофа відноситься до контуру і читається так: у замкненому контурі алгебраїчна сума комплексних діючих значень EPC або напруг джерел дорівнює алгебраїчній сумі комплексних значень спадів напруг на ділянках контуру

(2.54)

Відмітимо, що іноді доцільно розрахунок вести не в діючих значеннях, а в комплексних амплітудах. Все інше аналогічне колам постійного струму (див. 1.2, 1.4 - 1.7).

2.6. Резонанс у колах змінного струму

2.6.1. Резонанс напруг

Щоб дослідити резонанс напруг, необхідно мати котушку індуктивності і конденсатор, ввімкнути їх послідовно на джерело змінного струму і виконати умови, за яких можливий резонанс (рис. 2.27).

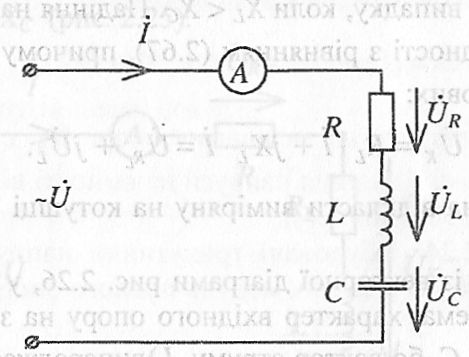
Рис. 2.27

Як було відмічено вище, резонанс настає у разі, коли виконується умова:

(2.71)

Ця умова може бути виконана двома способами:

а) необхідно мати можливість регулювати величини або (наприклад, мати котушку індуктивності з проміжними виводами обмотки або мати магазин ємностей);

б) для будь-яких фіксованих значень L та C необхідно мати можливість регулювати частоту напруги живлення джерела і отримання резонансної частоти.

Розглянемо умову резонансної частоти. Умову (2.71) через кутову частоту ω₀, очевидно, можна записати так:

(2.72)

Звідси

. (2.73)

Відмітимо, що зручно резонансну частоту позначити з індексом "0". Якщо ж нас цікавить резонансна частота , то , звідси:

(2.74)

Ще раз відмітимо, що у всі формули індуктивності та ємності слід підставляти в основних одиницях, тобто індуктивності L у генрі, ємності C у фарадах. Якщо задана L в мГн, то необхідний співмножник 10^-3, якщо ємність C задана у мкФ, то необхідний співмножник 10^-6.

На рис. 2.28 наведена векторна діаграма струму і напруг для режиму роботи схеми при виконанні умов резонансу напруг. При резонансі спад напруги на індуктивності дорівнює за величиною і протилежний за фазою спаду напруги на ємності . Тому повна напруга джерела дорівнює спаду напруги на активному опорі і співпадає за фазою з струмом .

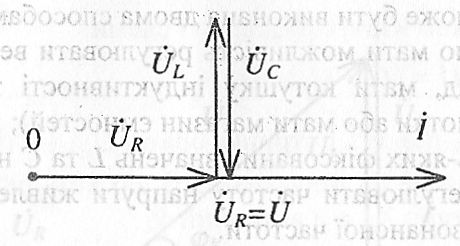
Рис. 2 28

Іншими словами, при резонансі струм і напруга джерела співпадають за фазою, тобто розглядувана схема послідовного з'єднання R, L, C зводиться до одного активного опору R (див. 2.5). Модуль повного опору схеми:

(2.75)

Таким чином, при резонансі опір кола мінімальний і дорівнює R. Отже, струм при резонансі буде мати найбільше значення. На рис. 2.29 наведені графічні залежності від частоти спадів напруг на індуктивності і ємності, а також характер зміни струму. Із цих залежностей видно, що резонанс настає при частоті ω₀, коли (точка "m"), струм І при цьому має найбільше значення, бо він обмежений тільки активним опором кола R.

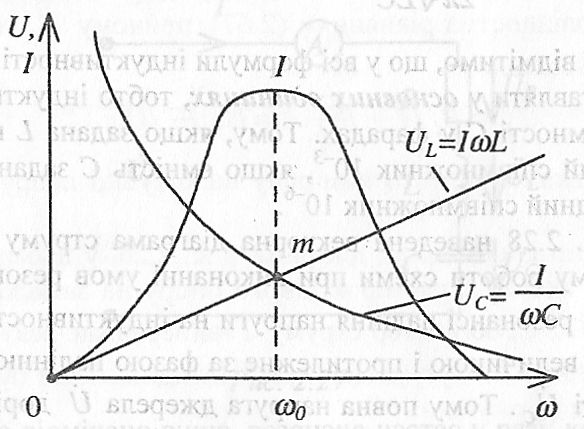
Рис. 2.29

При ідеальному резонансі (коли приймають R = 0) вхідний опір , а струм матиме нескінченно велике значення (теоретично).

Характеристичним або хвильовим опором ρ називають опір індуктивності і ємності при умові резонансу, тобто коли

, або .

Для індуктивності:

(2.76)

Для ємності:

(2.77)

Перевіримо розмірність ρ:

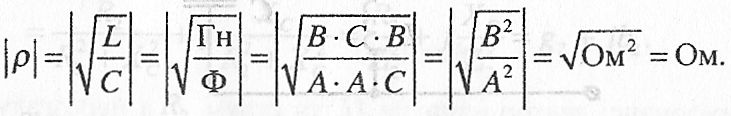
Добротністю контуру Q називається співвідношення характеристичного опору ρ(ρ₀) до активного опору R:

(2.78)

Значення Q означає кратність напруги на індуктивності та ємності у порівнянні з напругою джерела в момент резонансу. Так, якщо Q =10, то це означає, що при резонансі міжвиткова ізоляція котушки буде знаходитися під 10-кратним перенапруженням, і ця ізоляція може бути зруйнована.

Затуханням контуру d називають величину, яка обернена добротності Q:

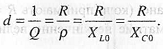(2.79)