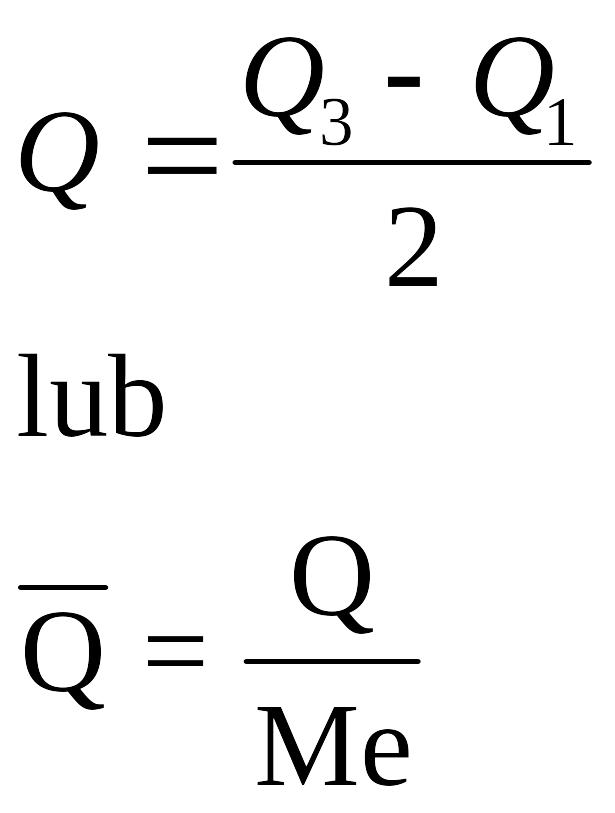Kwartyle

W statystyce często używane są także, obok mediany, inne średnie pozycyjne, a zwłaszcza kwartyle (czyli wartości ćwiartkowe), a niekiedy także decyle.

Kwartyle, to takie wartości cechy, które uporządkowaną populację dzielą na cztery równe części (tzw. ćwiartki).

Istnieją trzy kwartyle:

• pierwszy z nich dzieli populację na 1/4 populacji (Q₁),

• drugi - na dwie równe części (mediana) (Q₂ = Me)

• trzeci - oddziela 3/4 populacji o mniejszych od tego kwartyla wartościach cechy (Q₃).

DECYLE

Jeśli chodzi o decyle, to dzielą one uporządkowaną populację na 10 równych części, a stąd ich ilość wynosi 9, tj.

Kwantyle

• Wyznaczanie kwartyli, decyli, a także innego rodzaju średnich pozycyjnych, zwanych ogólnie kwantylami może mieć zastosowanie tylko do tych przykładów, gdy szereg rozdzielczy zawiera wiele wariantów (przedziałów klasowych) cechy, a populacja jest liczna. W tych sytuacjach cechę można traktować jako ciągłą i tylko do tego przypadku ograniczymy w dalszym ciągu ogólne uwagi o sposobie obliczania kwantyli.

• Jeśli kwantyl dzieli populację na k równych części (tzw. kwantyl rzędu k) i chcemy znaleźć w-ty z kolei kwantyl tego rzędu, to mieścić się on będzie w tym przedziale, którego skumulowana liczebność jest po raz pierwszy równa, lub większa od pewnej liczby, co można zapisać:

We wzorze tym symbol q oznacza numer klasy, do której należy interesujący nas kwantyl.

Wyznaczenie jakiegokolwiek w-tego kwantyla rzędu k w ramach danego przedziału, odbywa się przy użyciu wzoru przybliżonego. Oznaczmy ten kwantyl symbolem Q_w,k , mamy:

x_d - dolna granica przedziału zawierająca kwantyl,

(q-1) - numer przedziału poprzedzającego przedział z kwantylem,

D - długość przedziału zawierającego kwantyl,

n_d - liczebność tego przedziału.

Miary zróżnicowania cechy (dyspersji, rozproszenia)

1. Rozstęp I odchylenie ćwiartkowe

2. Wariancja I odchylenie standardowe

3. Współczynnik zmienności potrzeba badania zmienności

• Zawsze występuje zróżnicowanie cech badanych zbiorowości.

 Ta zmienność , lub jak inaczej mówimy – zróżnicowanie, dyspersja, stanowi o istocie statystyki.

 Bez zmienności w populacji, nie istnieje potrzeba badań statystycznych.

 Ze względu na występowanie zmienności zachodzi potrzeba posługiwania się wielkościami średnimi, pozwalającymi mierzyć ogólne poziomy wartości badanej cechy.

 Ale istnieje także potrzeba mierzenia zmienności badanych cech w różnych zbiorowościach.

1. Rozstęp I odchylenie ćwiartkowe

Najprostszą miarą zmienności jest rozstęp. Jest to różnica między największym i najmniejszym elementem.

R = x_max – x_min

Porównanie rozstępów między dwoma populacjami jest możliwe, gdy bierzemy pod uwagę tą samą cechę. Można także odnieść rozstęp do jakiejś miary średniej, np. do mediany, otrzymując stosunkowy rozstęp:

Często posługujemy się inną miarą, aby uniknąć wypływu wartości skrajnych, tj. odchyleniem ćwiartkowym i stosunkowym odchyleniem ćwiartkowym.

Odchylenie ćwiartkowe Q opiera się na kwartylach. Jest to połowa różnicy między trzecim i pierwszym kwartylem. Wykorzystujemy także stosunkowe odchylenie ćwiartkowe, tj. odchylenie ćwiartkowe w stosunku do mediany. Obydwa wzory podane są niżej.