7.8. Самоорганизующиеся нейронные сети Кохонена
Одной из главных задач, решаемых системой интеллектуальной поддержки, является задача распознавания ситуаций (образов). Эти ситуации не всегда могут быть априори классифицированы и предоставлены системе в виде набора шаблонов. На этот случай в системе должны присутствовать механизмы разбиения воспринимаемых ситуаций на классы (кластеризации) и последующей классификации вновь поступающих образов. Основой для построения таких механизмов могут служить самоорганизующиеся нейронные сети.
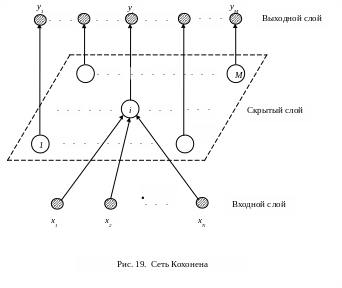
Классическим примером самоорганизующейся нейронной сети является сеть Кохонена (самоорганизующаяся карта признаков) [11, 19].
Нейронная сеть Кохонена относится к классу сетей прямого распространения. Она имеет единственный скрытый слой нейронов, представленный в виде одномерной или двумерной решетки (в принципе размерность решетки может быть и выше, случай двумерной решетки показан на рис. 19). Каждому скрытому нейрону соответствует свой выход сети. Нейроны входного слоя, количество которых равно размерности воспринимаемого образа, осуществляют функции приема и ретрансляции входных сигналов на все нейроны скрытого слоя (на рис. 19 это показано только для нейрона ). Число нейронов в скрытом слое (и, соответственно, число выходов сети) определяет количество кластеров, на распознавание которых ориентируется нейронная сеть.
Алгоритм,
обеспечивающий процесс самоорганизации
нейронной сети Кохонена, подбирая
синаптические веса связей между нейронами
входного и скрытого слоев
,
преследует цель отобразить множество
-мерных
входных векторов в двумерную карту
распределения нейронных активностей.
Каждый нейрон такой карты соответствует
определенному кластеру, объединяющему
в себе сходные по критерию близости
вектора. В качестве критерия близости
векторов
и
можно использовать евклидово расстояние
между ними
или
их скалярное произведение
(в смысле его максимума).
В основу алгоритма положены три механизма [19]:
механизм конкуренции;
механизм кооперации;
механизм адаптации.
Механизм конкуренции реализует конкурсный (конкурентный) метод, суть которого состоит в следующем.
Входной
вектор
и вектора синаптических весов входных
связей всех нейронов скрытого слоя (
)
предполагаются нормализованными. Для
каждого скрытого нейрона оценивается
величина его активности
.
Между нейронами осуществляется конкурс
на максимальное значение этой величины.
Нейрон
,
имеющий наибольшее значение нейронной
активности
,
объявляется победителем и наиболее
подходящим для данного вектора
.
Механизм
кооперации реализует принцип, согласно
которому наиболее возбужденный нейрон
усиливает (через синаптические веса)
не только себя, но и пространственно
близкие к нему нейроны. В связи с этим
вводятся понятия топологической
окрестности победившего нейрона и
функции окрестности
,
определяющей меру соседства нейрона
с
нейроном-победителем
.
В качестве последней часто используется
функция Гаусса
,
(7.12)
где
,
и
— дискретные
вектора, определяющие, соответственно,
позиции нейрона-победителя
и его нейрона-соседа
в решетке;
— эффективная ширина топологической
окрестности, определяющая минимальный
уровень функции окрестности, до которого
нейроны из топологической окрестности
участвуют в процессе обучения вместе
с нейроном-победителем.
В процессе обучения эффективная ширина топологической окрестности постепенно уменьшается, например, по закону
,
(7.13)
где
— дискретное
время;
—
начальное значение величины
;
— некоторая временная константа
(настроечный параметр алгоритма).
Таким образом, функция окрестности приобретает зависимость от времени в виде
,
(7.14)
где
определяется по формуле (7.13).
Механизм адаптации реализует определенную стратегию изменения (коррекции) весов синаптических связей. В ее основу может быть положено правило Хебба с некоторой дополнительной составляющей, учитывающей эффект забывания.
Правило Хебба говорит о том, что если предсинаптический и постсинаптический нейроны активизируются одновременно, то сила этой связи возрастает. В противном случае синапс ослабляется.
Эффект
забывания учитывается слагаемым
(входящим в общую формулу с отрицательным
знаком) в виде
,
где
—
вектор синаптических весов нейрона
;
— положительная
скалярная функция, определенная на
дискретном наборе выходных сигналов
нейронов (функция забывания) и
принимающая нулевое значение для
.
С учетом вышесказанного изменение (коррекция) вектора синаптических весов нейрона представляется следующей формулой:
,
(7.15)
где
— параметр
скорости обучения.
Если
в качестве функции забывания использовать
линейную функцию
и оценивать выходы нейронов функцией
окрестности, т.е. принять
,
то формула адаптации векторов синаптических
весов (7.15), с учетом необходимости их
нормирования, примет следующий вид:
,
(7.16)
где
— вектор, поданный
на вход сети в момент времени
;
— меняющийся во времени (постепенно
уменьшаемый) параметр скорости обучения.
В основу изменения параметра скорости обучения может быть положена функция
,
,
(7.17)
где
— исходное
значение параметра (в момент
);
— некоторая временная константа
(настроечный параметр алгоритма).
Формула
(7.16) применяется ко всем нейронам, лежащим
в топологической окрестности
нейрона-победителя
и
кооперирующимся с ним в обучении. Из
формулы видно, что вектора синаптических
весов кооперирующихся нейронов
смещаются в сторону входного вектора
со скоростью, пропорциональной
соответствующему им значению функции
окрестности (наиболее интенсивно это
происходит у нейрона-победителя
,
имеющего максимальное значение
).
Помимо рассмотренных архитектур ИНС, существует множество других, с которыми можно ознакомиться, обратившись к источникам [11, 12, 19].