Тема 17 Задания для решения на практическом занятии

1. а) за исключением прямых и ; б) за исключением точки ; в) полуплоскость ; г) полуплоскость ; д) полуплоскость ; е) за исключением гиперболы . 2. а) семейство гипербол , ; б) семейство прямых , ; в) семейство прямых , ; г) семейство парабол , ; д) семейство гипербол , ; е) семейство окружностей , . 3. а)  , ; б)  , ; в)  , ; г) , ; д)  , ; е)  , ; ж)  , ; з)  , ; и) , ; к)  , . 4. а) ; б) ; в)  ; г)  . 5. а)  , , ; б)  , , ; в)  , , ; г)  , , ; д)  , , ; е)  , , ; ж)  , , ; з)  , , ; и) , , ; к)  , , ; л)  , , . 6. , . 7.  , . 8. .

Задания для самостоятельной работы

1. а) за исключением прямой ; б) ; в) за исключением внутренности круга ; г) за исключением круга . 2. а) семейство прямых , ; б) семейство прямых , ; в) семейство прямых , ; г) семейство парабол , . 3. а)  , ; б)  , ; в) , ; г) , ; д)  , ; ж)  , ; з) , . 4. а)  , б)  ; в) .

Тема 18 Задания для решения на практическом занятии

1. а)  , локальный минимум, ; , локальный максимум, ; б) , локальный максимум, ; в) , локальный максимум, ; г) , локальный минимум, ; д)  , локальный минимум, ; е) , локальный минимум, ; ж)  , локальный минимум, ; з) экстремумов нет. 2. а)  , ; б)  , ; в)  , . 3. а)  условный максимум, условный минимум; б) точка условного экстремума ; в) точка условного минимума ; г) точки условного экстремума , , , . 4.  ден. ед. при , . 5. как . 6.  ; ; .

Задания для самостоятельной работы

1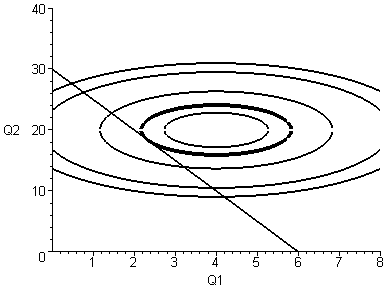 . а)  , локальный максимум (функцию следует представить в виде ; б) , локальный максимум; в) , локальный минимум; г) , локальный максимум; д) стационарных точек нет; е) экстремумов нет. 2. а) , ; б)  , ; в)  , . 3. а)  условный минимум; б)  условный минимум; условный максимум; в) условный минимум. 4.  ден. ед. при , . 5.  . 6. Решение. Заметим, что функция полезности представляет собой выпуклый вниз эллиптический параболоид с вершиной в точке . Множеством ее линий уровня (кривых безразличия) является семейство эллипсов ( ) с центром в точке (см. рис.). Задача оптимизации функции полезности (см. п. 18.4.5) сводится к отысканию минимума функции при ограничениях , , . Так как , , , то допустимое множество представляет собой треугольник, ограниченный прямыми , , , (см. рис.). В теории потребительского спроса утверждается, что оптимальное значение функции полезности достигается в том случае, когда потребитель тратит на приобретение товаров и весь свой доход . Следовательно, отыскание экстремума (минимума) функции полезности при ограничениях , , (на выпуклом множестве) сводится к отысканию экстремума (минимума) функции при условии (на границе выпуклого множества). Функция Лагранжа: , ее частные производные: , , , стационарная точка: . Таким образом, получили значения спроса, минимизирующие функцию полезности: , (соответствующая линия уровня касается линии ). Оптимальная полезность . Для определения эффектов замены составим функцию Лагранжа в общем виде: . Найдем ее частные производные: , , . Из системы уравнений выразим и , получим , . Согласно уравнениям Слуцкого (см. п. 17.6) эффекты замены можно рассчитать по формулам , ( ). Найдем частные производные , ( ) и их значения при , , : , , , , , . Подставим их и  , в уравнения Слуцкого, получим значения эффектов замены: , , , . Заметим, что , а  , следовательно, товары и взаимозаменямые, но представляются взаимодополняемыми без учета компенсации.