
- •2. Номенклатура и свойства показателей безотказности невосстанавливаемых объектов
- •2.1 Понятие невосстанавливаемого объекта
- •2.2. Свойства показателей безотказности невосстанавливаемых объектов
- •2.3. Вероятность безотказной работы
- •Интервалом (0, t) безотказной работы.
- •2.5. Средняя наработка до отказа
- •2.6. Интенсивность отказов
- •2.7. Основное уравнение надежности объектов
- •2.8. Статистическое определение оценок показателей безотказности
2.7. Основное уравнение надежности объектов
Это уравнение связывает значение ВБОР P(t), которую далее будем называть функцией надежности p(t) с функцией интенсивности отказов. Для получения основного уравнения надежности используем формулу (2.24.) интенсивности отказов:
![]() или
или
![]()
Учитывая, что
первая производная функции y=lnx
равна
![]() можно записать, приняв, что x=p(t):
можно записать, приняв, что x=p(t):
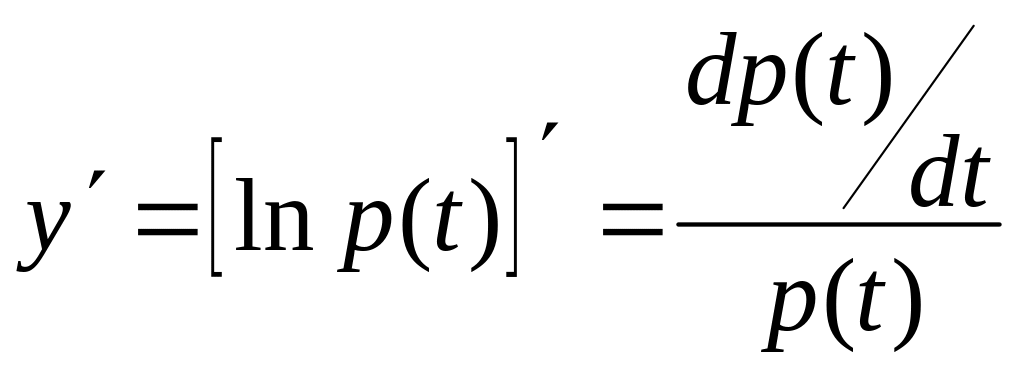 Следовательно, выражение (t)
можно переписать в виде:
Следовательно, выражение (t)
можно переписать в виде:
![]() (2.26.)
(2.26.)
Интегрируя в приделах (0, t) обе части равенства, получим с учетом того, что P(0)=1:
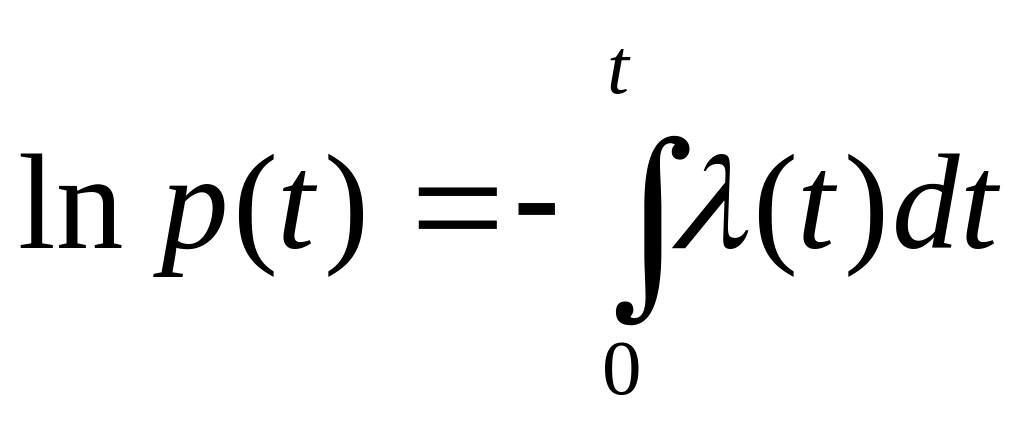 или
или
![]() (2.27.)
(2.27.)
Основное уравнение надежности показывает, что для получения функции надежности (т.е. функции ВБОР) необходимо число “е” возвести в отрицательную степень, равную интегралу в пределах (0, t) от функции (t). С учетом этого условная ВБОР в интервале (t, t+) может быть записана
![]() (2.28.)
(2.28.)
2.8. Статистическое определение оценок показателей безотказности
В результате
наблюдений над N
экземплярами объектов данного типа
определяются наработки до первого
отказа каждого экземпляра, в результате
чего получаем вариационный ряд: Т1,
Т2,…,
Тi,…,
ТN,
![]() - номер экземпляра объекта, Тi
- их наработка на отказ.
- номер экземпляра объекта, Тi
- их наработка на отказ.
Зададимся наработкой
t
и найдем число экземпляров n(t),
отказавших к моменту t.
Тогда оценки
![]() и
и
![]() определяются
в виде:
определяются
в виде:
![]() (2.29.)
(2.29.)
Следовательно, оценка ВБОР с учетом формулы (2.6.) определяется в виде:
![]() (2.30.)
(2.30.)
Для получения оценки интенсивности отказов необходимо задаться наработкой t и наработкой t+t>t и определить число экземпляров, отказавших к этим моментам: n(t) и n(t+t). Тогда оценка интенсивности отказов определяется по формуле:
![]() (2.31.)
(2.31.)
Числитель формулы (2.31.) показывает, какое число экземпляров отказало в интервале t. В знаменателе формулы разность N-n(t) показывает, какое число экземпляров еще не отказало к началу интервала нароботки и (t, t+t).
Очевидно, что
оценки
![]() ,
и
,
и
![]() показателей безотказности, полученные
по формулам (2.29)-(2.31), являются точечными,
т.е. определяют значения этих показателей
в виде одной точки функций P(t),
q(t)
и (t).
Для получения оценок указанных функций
в целом следует найти ряд точечных
оценок этих функций, по которым построить
сами функции в виде полигона, соединив
ломаной кривой полученные точечные
оценки.
показателей безотказности, полученные
по формулам (2.29)-(2.31), являются точечными,
т.е. определяют значения этих показателей
в виде одной точки функций P(t),
q(t)
и (t).
Для получения оценок указанных функций
в целом следует найти ряд точечных
оценок этих функций, по которым построить
сами функции в виде полигона, соединив
ломаной кривой полученные точечные
оценки.
Оценки функций можно получить в виде гистограмм функций. Для этого наработку 0…TN разбивают на 10…20 равных интервалов t, номера которых от j=1 до j=l. Затем определяют nj - число экземпляров, отказавших к началу j-того интервала, и nj - отказавших внутри j-того интервала. Находим точечные оценки для каждого интервала:
![]()
![]()
![]() (2.32.)
(2.32.)
Оценка средней наработки до отказа определяются по формуле
![]() (2.33.)
(2.33.)
где: Ti – наработка до отказа каждого экземпляра, номера которых от i=1 до i=N
Оценка дисперсии наработки до отказа определяется по формуле
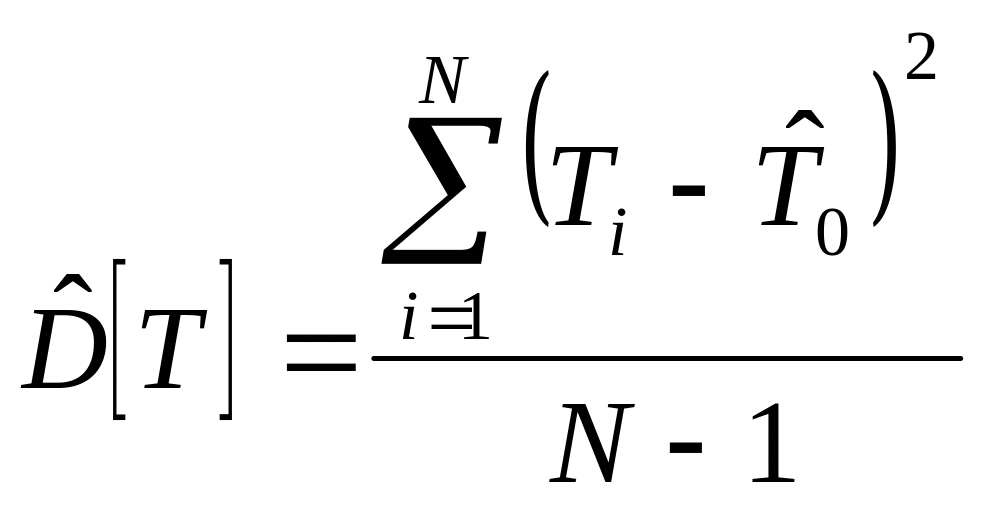 (2.34.)
(2.34.)
Оценка
![]() является средним арифметическим
наработок до отказа Ti.
Оценка
является средним арифметическим
наработок до отказа Ti.
Оценка
![]() находится, если извесна оценка
,
как видно из формулы (2.34). Оценка
является несмещенной, для чего знаменатель
формулы оценки равен N-1.
находится, если извесна оценка
,
как видно из формулы (2.34). Оценка
является несмещенной, для чего знаменатель
формулы оценки равен N-1.
