LB_CSAU4

Лабораторна робота № 4

Дослідження частотних характеристик цифрових систем

Мета роботи:

Закріплення та поглиблення знань студентів при вивченні і дослідженні частотних характеристик цифрових систем.

У результаті виконання роботи студенти повинні:

• уміти будувати амплітудно-частотні, фазочастотні та амплітудо-фазові-характеристики за відомою z-передаточну функцію;

• придбати практичні навички з побудови частотних характеристик цифрових систем в функціях псевдочастоти.

Вихідні дані

В ихідними даними для виконання роботи є структурна схема (рис. 4.1) та параметри (табл. 4.1) досліджуваної системи.

Таблиця 4.1

Параметри досліджуваних систем до лабораторної роботи № 4

№ з/п	Схема на рис. 3.1	К1	К2	К3	Т1, с	Т2, с	Т3, с	Т, с
1	А	0,5	1	2,5	1	2,5	-	0,025
2	Б	1	0,4	3	0,5	1	2	0,05
3	В	0,1	0,4	3	1	2	-	0,05
4	а	0,75	0,6	1,8	0,5	0,54	-	0,02
5	б	0,7	0,2	5	1	0,8	3	0,1
6	в	0,2	0,6	2	0,5	2,5	-	0,02
7	а	1	1,4	1,4	0,8	0,78	-	0,03
8	б	0,7	0,2	4	1	0,4	1,8	0,05
9	в	0,4	0,2	1,6	0,8	3,2	-	0,05
10	а	1,2	0,7	2,8	1,2	1,24	-	0,02
11	б	1,2	0,5	4	0,5	0,4	1,8	0,05
12	в	0,2	0,5	1,6	0,8	3,2	-	0,05
13	а	1	1,4	1,2	0,75	1,75	-	0,025
14	б	1	0,35	6	0,8	2	4	0,05
15	в	0,4	0,4	1	0,3	1,2	-	0,02
16	а	1,6	0,4	3,4	2	2,5	-	0,02
17	б	0,5	0,5	6	0,5	2	4	0,05
18	в	0,5	0,5	0,5	2	4	-	0,1

Порядок виконання роботи

При виконанні лабораторної роботи радимо додержуватися такого порядку:

1. Записати z-передаточну функцію зведеної безперервної частини цифрової системи.

2. Скласти розрахункову структурну схему, згідно з якою записати z-передаточну функцію та різницеве рівняння замкнутої системи.

3. Розрахувати на ЕОМ перехідний процес у досліджуваній системі при одиничному ступінчастому вхідному впливові.

4. Записати аналітичний вираз для амплітудно-фазової частотної характеристики, виконавши підстановку в дискретну передаточну функцію замкнутої системи

; (4.1)

5. На основі отриманого аналітичного виразу для амплітудно-фазової частотної характеристики побудувати амплітудно-частотну та фазочастотну характеристику замкненої цифрової системи за формулами

, (4.2)

, (4.3)

. (4.4)

На основі аналізу отриманих графіків АЧХ та ФЧХ цифрової системи визначити частоту повторення характеристик.

6. Записати аналітичний вираз для амплітудно-фазової частотної характеристики в функції відносної частоти , виконавши підстановку в дискретну передаточну функцію замкнутої системи

. (4.5)

7. На основі отриманого за формулою (4.5) аналітичного виразу для амплітудно-фазової частотної характеристики побудувати амплітудно-частотну та фазочастотну характеристику замкненої цифрової системи в функціях відносної частоти та визначити період їх повторення; привести деталізовані графіки АЧХ та ФЧХ в діапазоні змінення відносної частоти 0 ≤   ≤π.

8. Побудувати амплітудно-частотну та фазочастотну характеристику в функціях псевдочастоти. Для цього необхідно

• в дискретній передаточній функції 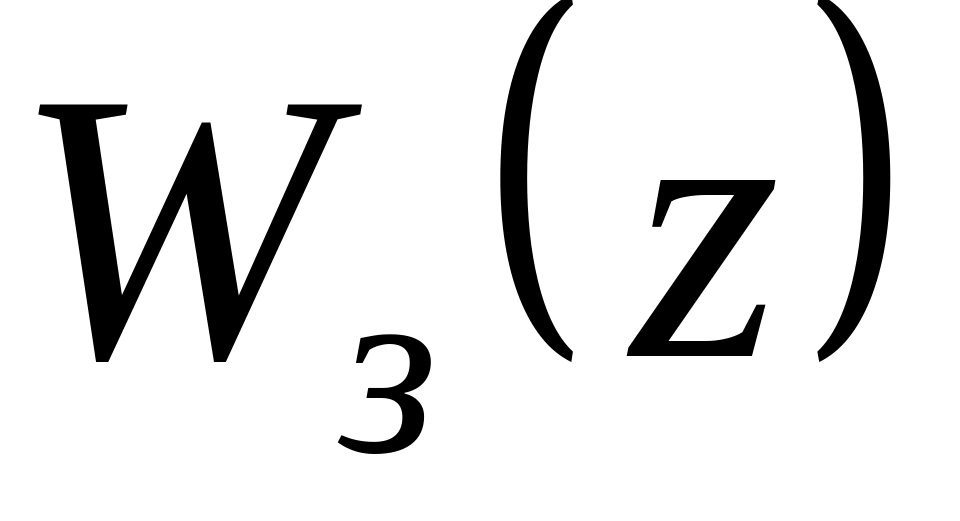за допомогою білінійного w-перетворення

(4.6)

перейти до w-площини;

• здійснивши підстановку 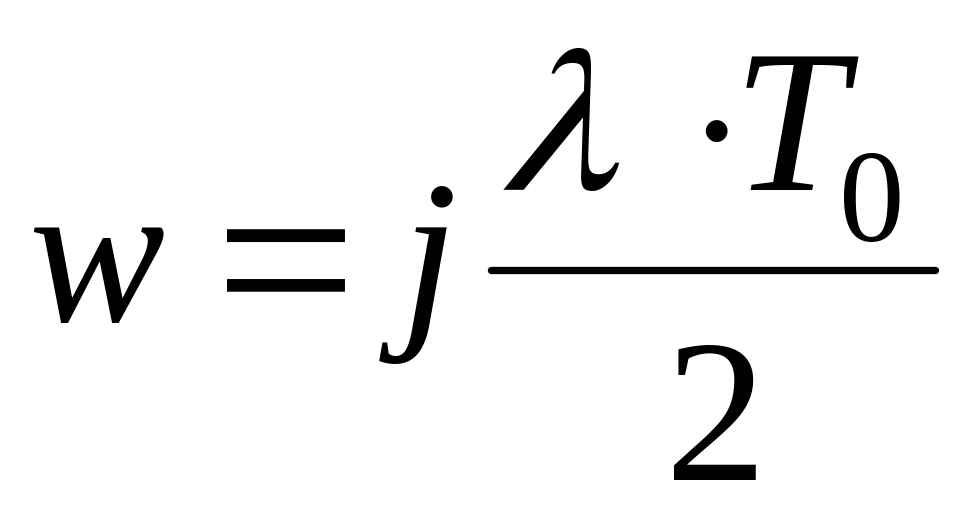, отримати комплексну функцію абсолютної псевдочастоти

. (4.7)

• за формулами

, (4.8)

, (4.9)

, (4.10)

побудувати АЧХ, ФЧХ та ЛАЧХ цифрової системи в функціях псевдочастоти.

9. Зробити висновки з одержаних результатів.

Приклад 4.1. Для цифрової системи, структурна схема якої задана на рис. 4.2а, знайти z-передаточну функцію W_ПН(z) зведеної безперервної частини. Скласти розрахункову структурну схему згідно з z-передаточними функціями цифрового регулятора та зведеної безперервної частини. Користуючись таблицями зворотного z-перетворення, знайти аналітичний вираз для розрахунку перехідної характеристики замкнутої системи. Визначити також усталену похибку при одиничному ступінчастому вхідному впливові. Побудувати частотні характеристики цифрової САК.

Р озв’язання

Дискретна передаточна функція зведеної безперервної частини

Складаємо розрахункову структурну схему системи (рис. 4.2, 6), згідно з якою запишемо дискретну передаточну функцію замкненої системи.

Дискретні передаточні функції цифрового регулятора D(z) та зведеної неперервної частини Wзн (z) матимуть вигляд

, (4.11)

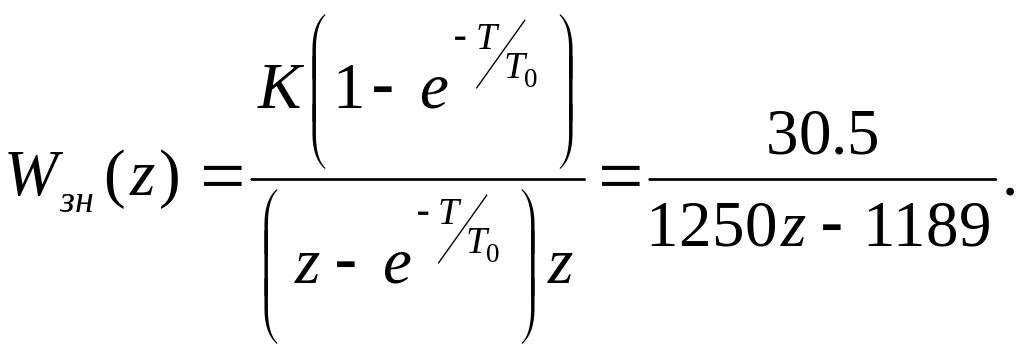(4.12)

Дискретна передаточна функція розімкнутої системи

. (4.13)

Дискретна передаточна функція замкнутої системи

. (4.14)

При запишемо z-зображення керованої величини системи

. (4.15)

Скориставшись методом невизначених коефіцієнтів, вираз (3.14) можна записати так

Згідно з таблицею зворотного z-перетворення записуємо аналітичний вираз для кривої перехідного процесу

. (4.16)

Приклад програми в MathCAD

1. Дискретна передаточна функція приведеної безперервної частини

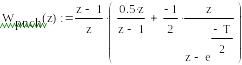
Дискретна передаточна функція регулятора

2. Дискретна передаточна функція замкненої системи

3. Знаходимо z-зображення вихідної величини

Знаходимо решітчасту функцію та будуємо графік перехідного процесу в замкнутій системі

4. Для знаходження амплітудно-фазової частотної характеристики виконуємо підстановку в дискретну передаточну функцію замкнутої системи

5. Будуємо АЧХ

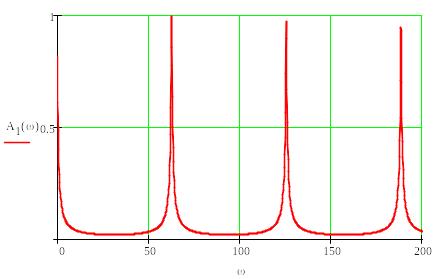
Будуємо графік фазочастотної характеристики на інтервалі

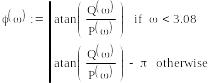
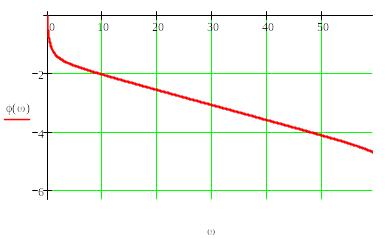
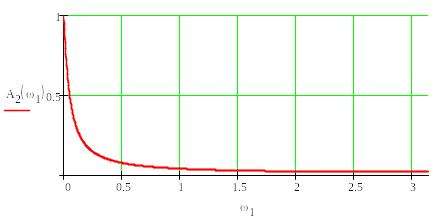
6. Будуємо частотні характеристики в функції відносної частоти на інтервалі .

Для знаходження амплітудно-фазової частотної характеристики в функції відносної частоти виконуємо підстановку в дискретну передаточну функцію замкнутої системи

7. Будуємо АЧХ

Будуємо фазочастотну характеристику

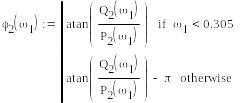
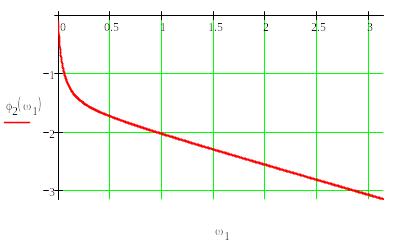
8. Будуємо частотні характеристики цифрової системи в функціях псевдочастоти λ. Для цього необхідно в дискретній передаточній функції за допомогою білінійного w-перетворення перейти до w-площини

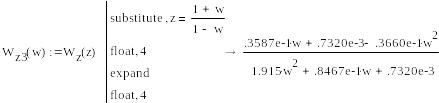
Далі, здійснивши підстановку , отримати комплексну функцію абсолютної псевдочастоти

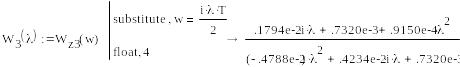
Побудувати графік амплітудно-фазової характеристики в функції псевдочастоти

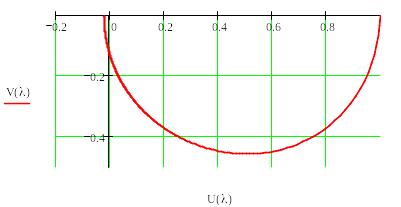
Будуємо АЧХ в функції псевдочастоти

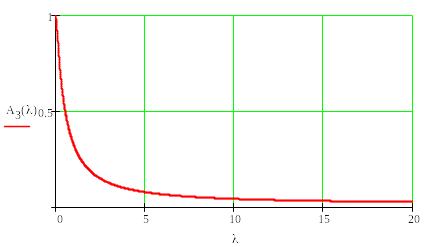
Будуємо ФЧХ замкненої системи в функції псевдочастоти

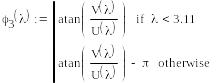
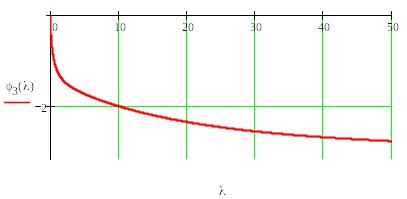
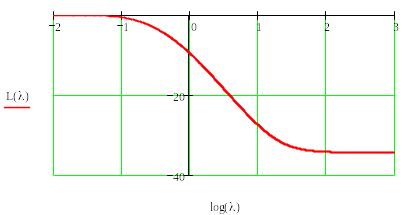
Будуємо ЛАЧХ замкненої системи в функції псевдочастоти