Перша теорема двоїстості.

1. Якщо одна із задач І чи І′ має оптимальне рішення, то і інша має оптимальне рішення, причому оптимуми цих задач співпадають.

2. Якщо Ц.Ф. однієї із задач необмежена зверху (для задачі І), чи знизу (для задачі ІІ) до друга задача недопустима.

Примітки.

Т, обернена до другої частини не вірно,а саме можна навести приклади, коли і пряма і двоїста задача недопустимі.

Доведення:

Враховуючи взаємну двоїстість задач І і І′ можна все довести для задачі І. Нехай задача І має оптимум рішень і ми знайшли його симплекс-методом.

х⁰ = (х₁⁰, х₂⁰, ..., х_п⁰) його базис складають А_i1, А_i2,….,А_im тоді ∆j ≥ 0 → z_j-c_j ≥0, z_j ≥ c_j

За модифікованим симплекс-методом z_j=(C_баз *В^-1) А_j, C_баз *В^-1₌Ω

(z_1, z₂,..,z_n) = (C_баз *В^-1) А

Таким чином двоїста задача має вигляд (b,y)→min

Y^TA ≥ C, то ми можемо записати ΩА ≥ (С_1, С₂,..., С_n), а це значить що вектор Ω є допустимим розв’язком двоїстої задачі.

Доведемо, що Ω є і оптимальним розв’язком. Для цього використаємо лему. Знайдемо значення Ц.Ф. при Ω.

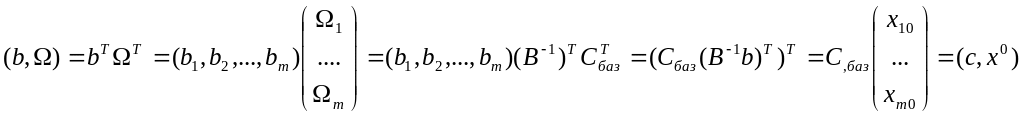Отже для допустимих рішень х₀ задачі І і Ω задачі І^/ співпадають. За лемою значить, що Ω - оптимальний розв’язок.

Доведення ІІ-ї частини.

Нехай, наприклад Ц.Ф. задачі І необмежена зверху на допустимій множині. Потрібно довести , що не має допустимих розв’язків. Допускаємо, що І^/ має допустимі розв’язки, наприклад y. (b, y) = N

Оскільки за умовою Ц.Ф. задачі І необмежена зверху, тоді існує такий допустимий розв’язок х задачі І, що виконується (с, х) > N = (b, y), а це суперечить лемі. Обернене доводиться аналогічно.

Примітка.

Попутно ми довели, що якщо х⁰ – оптимальний опорний розв’язок задачі І, то вектор його симплекс-множителів Ω = C_баз *В^-1 є оптимальним розв’язком двоїстої задачі.

Друга торема двоїстості. (скорочена форма)

Нехай х і у - допустимі розв’язки задач І і І^/ , то х і у тоді і тільки тоді є оптимальними розв’язками цих задач, коли виконується умова:

(a_1jy ₁ + a_2jy + …+ a_mjy -c_j) x _j=0, j =1..n

Симетричні двоїсті задачі.

Нехай тепер дана будь-яка ЗЛП в симетричній формі.

x_j ≥0, j = 1..m, i = 1..m m+1 – мірний вектор

- j-та технологія

Але тепер будемо вважати, що любий з m – факторів може як і вироблятися так і споживатися.

Фактор а_ij .

Якщо а_ij > 0 , то і-тий фактор витрачається у кількості а_ij за одиницю часу.

Якщо а_ij<0, то і-ий фактор виробляється в j- тій технології.

Якщо а_ij = 0 , то даний фактор не враховується.

Фактор с_j .

Якщо с _j > 0 , то рахується, що ефект j-тої технології за одиницю часу.

Якщо с _j <0, то це збитки j-тої технології за одиницю часу.

Якщо с _j = 0 , то спосіб нейтральний.

Фактор b_i .

Якщо b_i > 0 , то і-тий фактор існує у кількості b_i.

Якщо b_i <0, то будемо рахувати, що і-ий фактор повинен бути в виробництві у кількості b_i.

Якщо b_i = 0 , це означає, що і-го ресурсу в наявності не має, але він і не потрібен за планом.

Тоді max Ц.Ф. прагне максимізувати сумарний ефект системи.

х_ij – інтенсивність використання технології.

і-те обмеження означає, що якщо права частина додатна , то і-тий ресурс витрачається. Якщо від’ємна, то він виробляється в кількості b_i.

Означення:

Невиродженим п.д.о.р. будемо називати таке п.д.о.р. , для якого всі набрані оцінки ∆j > 0 .

Теорема 1. (критерій оптимальності п.д.о.р.)

Якщо п.д.о.р. є допустимим ,то воно є оптимальним розв’язком даної задачі , так як розглядається тільки п.д.о.р. і ∆j ≥ 0, то ця теорема випливає із звичайного критерію оптимальності.

Теорема 2. (про можливість „поліпшення” п.д.о.р.)

Якщо дане п.д.о.р. таке, що існує хоча б одна координата х_r0 < 0 і така, що серед х_rj , (j=1..n ) є від’ємна , то ми отримаємо краще п.д.о.р., якщо зробимо заміну в базисі вектор А_ik таким вектором А_j , для якого оцінки:

для всіх j, для яких j, х_rj < 0 (j ≠ s)

Примітки.

В цій теоремі існує не вироджене зауваження. Кращім є та , для якого значення Ц.Ф. менше. Це відповідає тому, що в двоїстій задачі ми отримуємо всі менші рішення (вона на min).

Теорема 3. (про недопустимість задачі.)

Якщо дана п.д.о.р така, що існує хоч одна х_к0< 0 для якої всі х_kj ≥ 0, то дана задача не має допустимих розв’язків (якщо задача не вироджена то через кінцеву кількість кроків ми або отримаємо оптимальний розв’язок, або переконаємося в недопустимості. В випадку виродженої задачі процес може зациклитися. Але є спеціальне правило вибору вектору, що вводиться в базис, котрий гарантує від за циклювання.

Із цих теорем випливають алгоритми двоїстого симплекс-методу.