Двоїстість лінійного програмування.

Відомо, що з кожною задачею лінійного програмування пов’язана інша, дані якої пов’язані з попередньою ( якщо там оптимум, то і тут оптимум і т.д.) - вона називається двоїстою.

Нехай дано канонічну ЗЛП. (1)

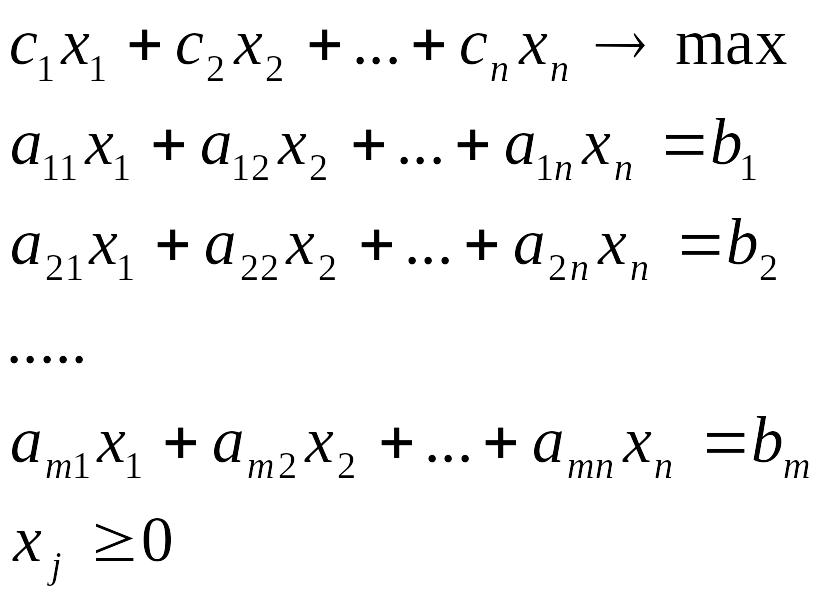
Двоїстою до неї називається задача (1^*)

М атриці ніби транспонуються. Але обмежень на знак змінних у двоїстій задачі не має. Замість рівняння отримуємо нерівність, замість максимума маємо мінімум.

Приклад

Побудувати двоїсту задачу до наступної.

Ч и в матричному вигляді:

Майже допустиме рішення будемо називати майже допустимим опорним рішенням (м.д.о.р.), якщо вектори а_ij відповідні до його ненульових координат лінійно - незалежні.

Базисом м.д.о.р. будемо називати будь-який упорядочений набір із m лінійно - незалежних векторів А_j серд яких знаходяться всі вектори А_j ,відповідні до всіх ненульових координат даного м.д.о.р.

В основі алгоритму двоїстого симплекс методу лежать 3 теореми:

Будемо розглядати тільки такі м.д.о.р. для котрих оцінки векторів А_j невід'ємна, тобто

д е i_1, i_2, i₃…i_m - номери базисних векторів м.д.о.р. (це відповідає тому, що вектор С_баз В^-1 є допустимим рішенням двоїстої задачі. )

Симетричні двоїсті задачі. З адача іі

Д воїста для неї форма:

Отже для задачі ІІ двоїста задача ІІ^":

З адачі ІІ і ІІ^" складають симетричну пару двоїстих задач.

Лемма та обидві теореми двоїстості є вірними і для симетричних задач, але при цьому запис другої теореми дещо змінюється. А саме , нехай дано дві задачі ІІ і ІІ^" х допустиме рішення ІІ, y - задачі ІІ^" .

x,y - тоді і тільки тоді будуть оптимальним рішенням, коли виконуються дві групи умов:

Двоїстий симплекс - метод.

Аналогічно до звичайного симплекс - метод заключається у посідовному переході від одного n-вимірного вектора до іншого, причому правила гарантують, що через кінцеве числр кроків ми отримуємо або оптимальний вектор , або переконуємося, що задача не має границь.

На відміну від симплекс методу тут послідовні вектори не мають бути допустимі, але як тільки отримуємо допустимі - вони же і оптимальні.

Виявляється, що для задачі І^” (якщо її привести до еквівалентної канонічної форми) двоїстою буде задача, еквівалентна до задачі І.

Розв’язок задачі:

В задачі на мінімум все так само, але z ' =z-Θ∆j

∆j - вибираємо максимум із додатних, тоді значення ц. ф. зменшиться . Таким чином задача І і І^” складають з точністю до еквівалентності пару взаємо двоїстих задач ( несиметричну пару). В матричному вигляді:

Від задачі І^/ перейшли до задачі І.

Лемма.

Нехай - будь-який допустимий розв’язок задачі І, а - будь-яке. Тоді виконується нерівність (с, )≤ (b, ) при любому допустимому розв’язку.

Якщо для будь-яких , виконується (с, )= (b, ), то , - оптимальний розв’язок для такої задачі.

Доведення.

Нехай =( ₁, ₂, …, _n) допустимий розв’язок задачі І.

= ( ₁, ₂, .., _n) допустимий розв’язок задачі І^/

Підставимо в границі задачі І. Отримуємо :

Перетворюємо :

за умовою двоїстої задачі.

Значення Ц.Ф. прямої задачі ≤ значенню Ц.Ф. двоїстої задачі.

Доведемо другу частину.

(с, х) =(b, y) нехай ця рівність зберігається, але y і х не оптимальний розв’язок.

Нехай існує х′ , що (с, х′) › (с, х ) = (с, у ) Це перечить першій частині леми. Аналогічно доводиться, що y  оптималене для задачі І′.