Лекція № 4

Доведення.

Необхідність:

Нехай вектори з рівності (6.1) А_i1, А_i2, …, А_im знову базис і нехай вектори x_ks = 0 (доведення від противного). Тоді рівність (6.1) означає, що ці вектори лінійно незалежні. Маємо протиріччя.

Достатність:

Нехай дано x_ks  0. Доведемо, що вектори А_i1, А_i2, …, А_im лінійно незалежні.

Припустимо, що вони лінійно залежні, тобто ₁А_i1+₂А_i2+…+_mА_im= 0, де не всі _і дорівнюють нулю. Тоді, _к0, інакше б вектори А_i1, А_i2, …, А_im були б лінійно залежні. Виразимо звідси А_s:

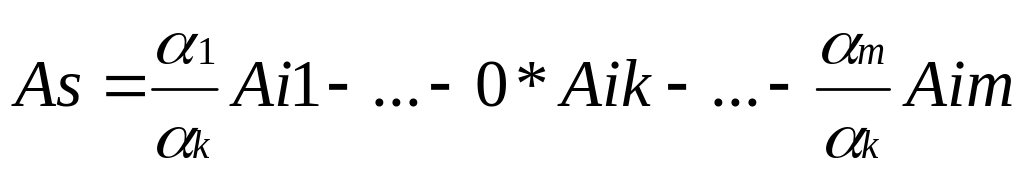(6.2).

Тоді для вектора А_s маємо два розкладення (6.1) та (6.2), причому в (6.1) коефіцієнт при А_ік не дорівнює 0, а в іншому – дорівнює. Отримали протиріччя. Лема доведена.

Основні формули симплекс – методу.

Нехай маємо систему векторів А1, А2, …, Аl і нехай вектори А_i1, А_i2, …, А_im складають базис.

Задача: які коефіцієнти А_s будуть в новому базисі.

З відношення (6.1) отримаємо

(6.3).

Таким чином, для вектора, який виводиться, отримаємо координати

(6.4).

Розглянемо координати довільного вектора Aj з розкладенням

A_j = x_1jA_i1 + x_2jA_i2 + …+ x_rjA_ir + …+ x_mjA_im (6.5).

Підставимо в (6.5) для Air його вираз з (6.3) і отримаємо:

(6.6).

Отже, коефіцієнти нового базиса:

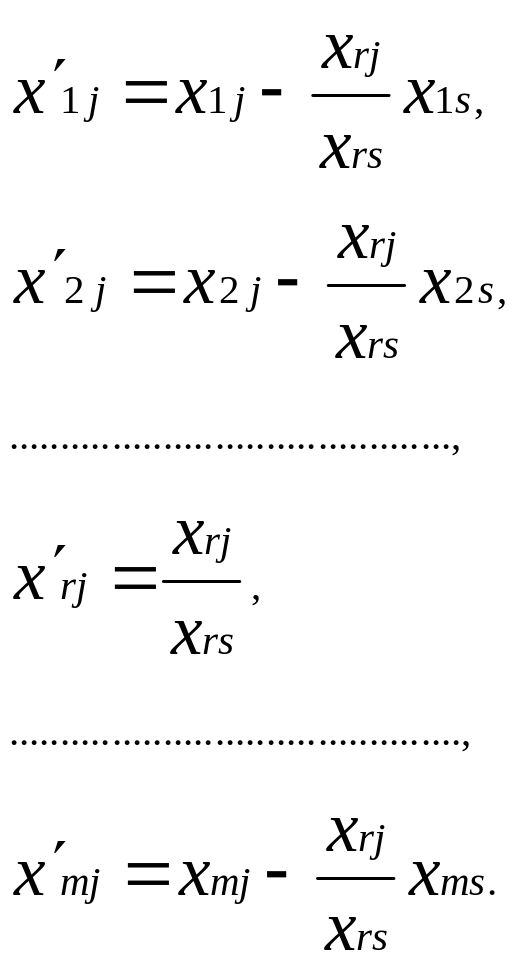(6.7)

Звідси маємо, що система (6.7) – основна формула симплекс – методу, де

x_kj – стара координата,

x_kj – нова координата,

x_ks – координата вводимого вектора,

x_rs – ведучий елемент.

Записуємо отримані дані в вигляді таблиці.

	А1	А2	…	Аs	…	An
Ai1	X11	X12	…	X1s	…	X1n
…
Air	Xr1	Xr2	…	Xrs 1	…	Xrn
…
Aim	Xm1	Xm2	…	Xms	…	Xmn

Виділимо x_rs – ведучий елемент. Тоді As – ведучій стовпчик, а Air – ведуча стрічка. Нові елементи вираховуються за правилом хрест – на – хрест:

.

Основна теорема симплекс – методу.

Нехай дана канонічна невироджена ЗЛП з слідуючою правою частиною:

.

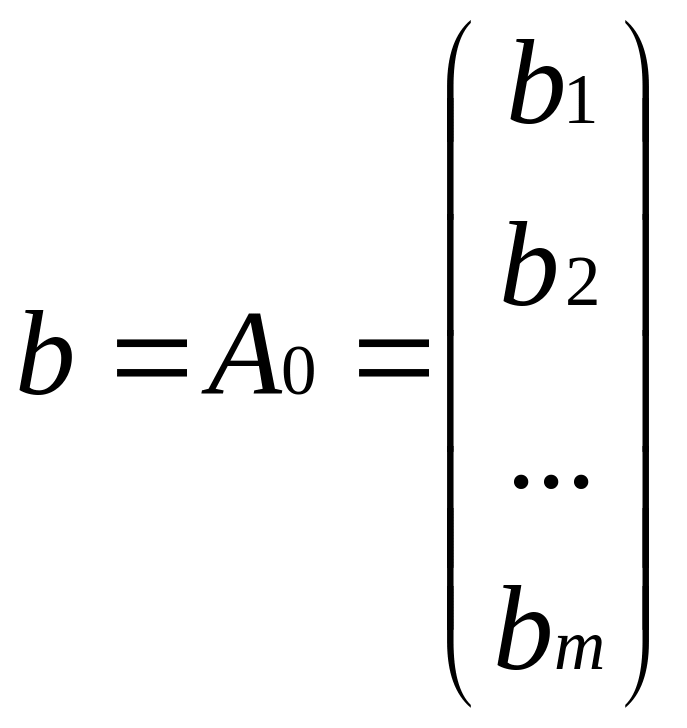Нехай дано опорний розвязок цієї задачі:

х = (х₁, х₂, …, х_m, 0,…, 0)

і нехай А1, А2, …, Аm – базис цього розвязку.

Тоді ЦФ буде дорівнювати

f(х) = c₁х₁+ c₂х₂+ …+ c_mх_m.

Розклад за базисом:

А0= А₁х₁+ А₂х₂+ …+ А_mх_m.

Нехай ми вирішили вектор Аs внести до базису, а Аr – вивести. Тоді:

1. Xrs  0 (за лемою);

2. Новий розвязок повинен бути допустимим.

Лекція №5

Знайдемо за основними формулами координати нового опорного розвязку в новому базисі А1, А2, …, Аm. Нехай

х_к0 (к = 1, m) – координати А0 в старому базисі,

х_к0 (к = 1, m) - координати А0 в новому базисі.

(7.1).

Для того, щоб новий розвязок був допустимим, необхідно щоби х_к > 0, х_r0 >0  х_rs > 0.

Для відємних х_ks в формулі умова х_к > 0 виконується автоматично. Якщо х_к > 0 , то

(7.2).

Для того, щоб новий розвязок був допустимим і опорним необхідне виконання двох умов:

1. х_rs > 0,

2. .

Обираємо r, s таким чином, щоб при виконанні умов (1) і (2) новий опорний розвязок був би кращим ніж попередній.

Запишемо новий опорний розвязок:

.

Якщо s таке, що z_s – c_s = ∆s < 0, то z_s > z_s, де ∆s – оцінка відповідного вектора.

Теорема 1 (про можливість отримання опорного розвязку).

Якщо даний опорний розвязок такий, що серед оцінок ∆s є відємні і така, що серед х_rs є х_rs > 0, то ми отримаємо найкраще опорний розвязок, або замінимо вектором As такий вектор Air старого базису, для якого .

Домовимось, що дані, повязані з опорним розвязком, зводити до таблиці.

Повна симплекс – таблиця.

№ п/п	Базис	Cj		C1	…	Cs	…	Cn
			A0	A1	…	As	…	An
1	Ai1	Ci1	X10	X11		X1s		X1n
2	Ai2	Ci2	X20	X21		X2s		X2n
…	…	…	…	…		…		…
m	Aim	Cim	Xm0	Xm1		Xms		Xmn
				∆1		∆s		∆n
			Zj-Cj

В стовпчику А0 знаходяться значення невідомих даного опорного розвязку (m невідомих), інші – дорівнюють 0.

Теорема 2 (про умови оптимального опорного розвязку).

Якщо для даного опорного розвязку всі оцінки ∆j  0, то ций опорний розвязок - оптимальний.

Теорема 3 (про признак необмеженості ЦФ).

Якщо для даного опорного розвязку існувала хоча б одна така відємна оцінка ∆s<0, для який всі Xks 0, то це означає, що ЦФ даної ЗЛП не обмежена зверху на допустимій множині.

Висновки: таким чином, в невиродженій задачі для будь – якого даного опорного розвязку виконуються або умови теореми 1, або теореми 2, або 3. Якщо конкретно виконуються умови теореми 2, чи 3, то задача розвязана. Якщо має місце умова теореми 1, то переходимо до кращого опорного розвязку. Для нього знову виконується теореми 1, 2, чи 3. Кількість різноманітних базисів обмежена. Базиси не можуть повторюватись. Таким чином, якщо задача не вироджена, то через обмежену кількість переходів (ітерацій) до кращого розвязку процес закінчиться.