Задачі про призначення.

Маємо таку перестановку (p_1…..p_n) із чисел 1, 2, 3, ,n , яка досягає мінімум по всім перестановкам c_ib_i. Перестановка може бути представлена точкою в n–вимірному евклідовому просторі у вигляді матриці:

Введемо змінні:

Очевидно , що виконується 4.1.6.

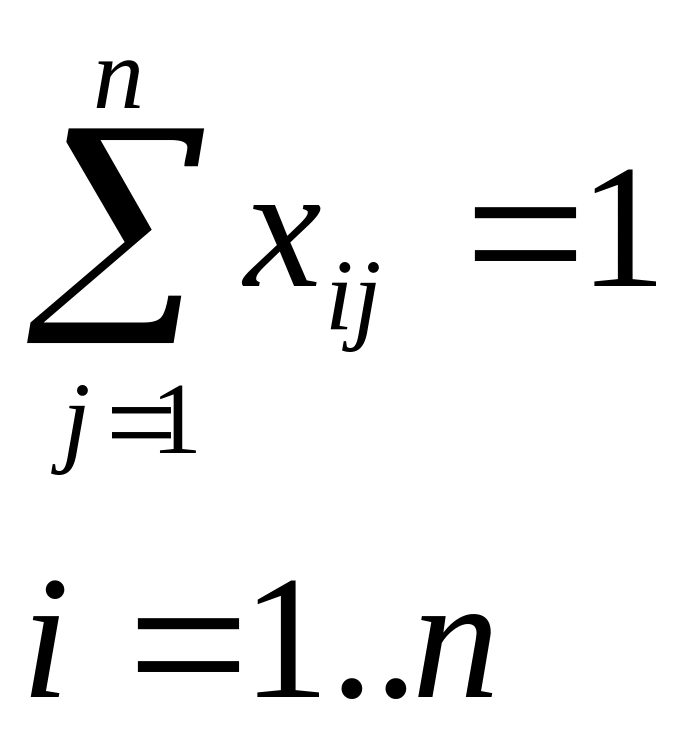(4.5)

Тоді задача заключається у винайденні таких чисел х_ij, при яких досягається мінімум функції при умовах 4.5.

Хоча умови цілочисельності х_ij в обмеженнях 4.5 у явному вигляді немає , але воно виконується, оскільки задача про призначення є частковим випадком транспортної задачі. Добрим методом є Угорський метод.

Задача про комівояжера.

Маємо місто. Задана матриця – відстань між містами. Виїжджаючи із першого міста А₀ комівояжер повинен побувати в усіх інших містах і повернутися в місто А₀. Визначити в якій послідовності потрібно відвідати всі міста комівояжеру, щоб сумарна пройдена відстань була мінімальною.

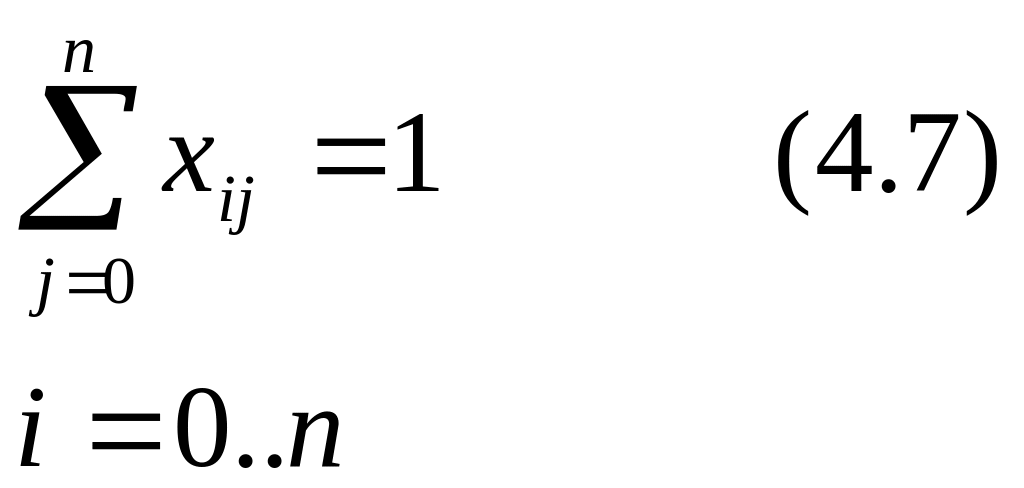
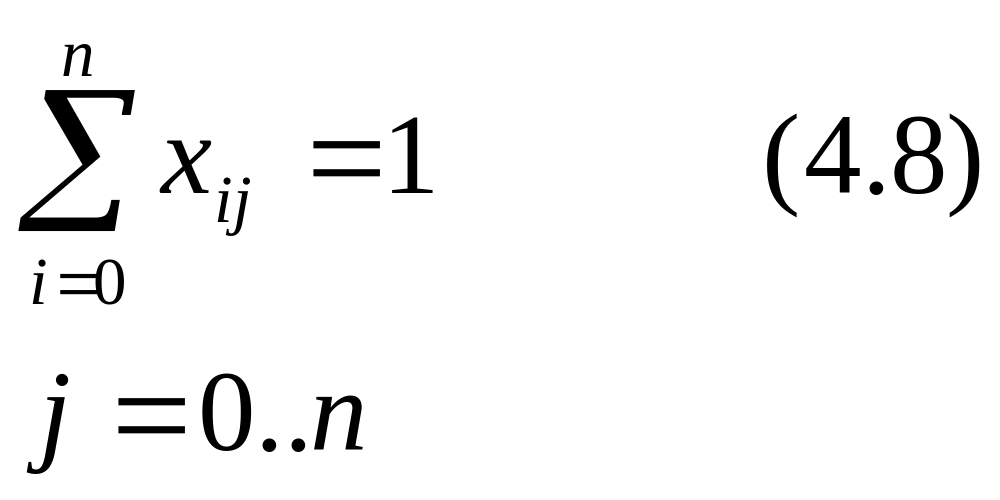
U_i – U_j + nx_ij ≤ n-1, i, j = 0..n, i ≠ j , (4.9)

Умова 4.7 означає, що він виїжджає із кожного міста один раз, а умова 4.8 означає в’їжджає в кожне місто один раз. Умова 4.9: можна знайти U_i – U_j, що буде виконуватися замкнутий цикл.

Метод відокремлюючих площин.

Розроблений Р. Гомори. Для задачі ЦП відповідно ідея покладенна в основу Данцигом.

Нехай необхідно розв’язати ЗЦП.

,х_і –цілі, j – 1..n (4.12)

Відкинемо на час умову чисельності і знайдемо оптимальний опорний план. Якщо він задовольняє умову чисельності, то даний план є шуканим. В оберненому випадку потрібно сформулювати додаткову течію ,в якій будь-який цілочисельний план не задовольняє знайдений не цілочисельний план.