5. Прямоугольная система координат

Рассмотрим частный случай аффинной системы координат. Выберем на плоскости точку О и ортонормированный базис , где , .

Определение 7.

Тройка называется прямоугольной (декартовой) системой координат в плоскости или прямоугольным репером.

Обозначается .

Точка О – начало координат, векторы ,  – базисные, перпендикулярные прямые, проходящие через точку О параллельно базисным векторам – координатные оси: ось абсцисс х и ось ординат.

Для построения точки достаточно построить прямоугольник ОМ_хММ_у с диагональю ОМ.

6. Метрические задачи

В прямоугольной декартовой системе координат можно решать все перечисленные выше аффинные задачи на взаимное расположение точек на прямой и плоскости, а также задачи на вычисление расстояний и углов – метрические.

Задача 10. Вычисление расстояния между двумя точками

Дано: , М₁(х₁; у₁), М₂(х₂; у₂)

Найти: расстояние .

Р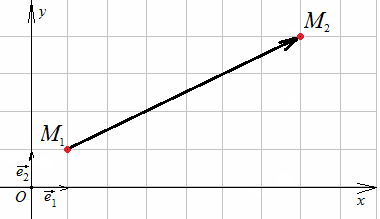 ешение. Расстояние между двумя точками М₁ и М₂ вычислим как длину отрезка М₁М₂ (рис.1.13), равную длине (модулю, абсолютной величине) вектора :

.

, значит,

.

Рис.1.13.

Тогда

(13)

Расстояние между двумя точками плоскости равно квадратному корню из суммы квадратов разностей одноименных координат.

Пример 6.

Дано: М₁(6; 0), М₂(–2; 1).

Найти: расстояние М₁М₂.

Решение.

.

.

Задача 11. Вычисление площади треугольника

Дано: , А(х₁; у₁), В(х₂; у₂), С(х₃; у₃).

Найти: площадь треугольника АВС.

Решение (рис.1.14).

Рис.1.14.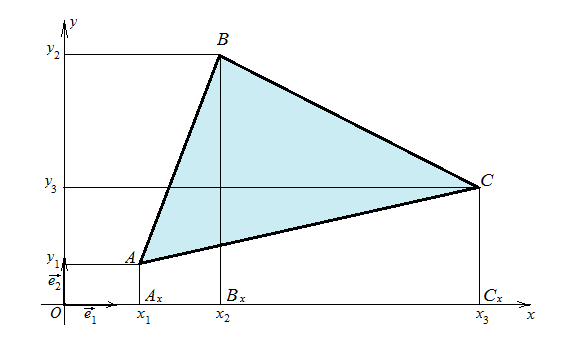

.

Вычислим площади трапеций А_хВ_хВА, В_хС_хСВ, А_хС_хСА по формуле :

,

аналогично , .

Тогда

.

Точки А, В и С могут располагаться иначе, а определитель, составленный из их координат – положительным или отрицательным числом, поэтому

. (14)

Если точки А, В и С лежат на одной прямой, то S=0 и, наоборот.

Пример 7.

Дано: А(6; 0), В(–2; 1), С(2; 7).

Найти: .

Решение.

. .

Литература и задания практикума (по УМК):

[2]	гл.1, §1	№ 9-14
[10]	гл.1, §1	№ 1-25
[2]	гл.1, §1	№ 15-25,37-39
[10]	гл.1, §1	№ 41-61,73-85

2. Данко П.Е. Высшая математика в упражнениях и задачах : в 2-х частях : учеб. пособие / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высшая школа, 1998. – Ч.1.

8. Сборник задач для самостоятельной работы по геометрии / авт.-сост. Т.М. Соромотина. – 2-е изд. – Пермь : Изд-во ПГПУ, 2008.

10. Цубербиллер О.Н. Сборник задач и упражнений по аналитической геометрии / О.Н. Цубербиллер. – 32-е изд. – СПб. : Лань, 2005.

Практикум 1

1. Постройте в аффинной системе координат точки A(3; 5), B(–4;–2), C(1;–3).

2. Выясните лежат ли точки A(3; 5), B(–4;–2) и М(9; 11) на одной прямой.

3. Найдите координаты точки К – середины отрезка АВ, если A(3; 7) и B(1; 7).

4. Найдите координаты точки М, которая делит отрезок АВ, где А(3; 5), В(9; 8), в отношении: а) 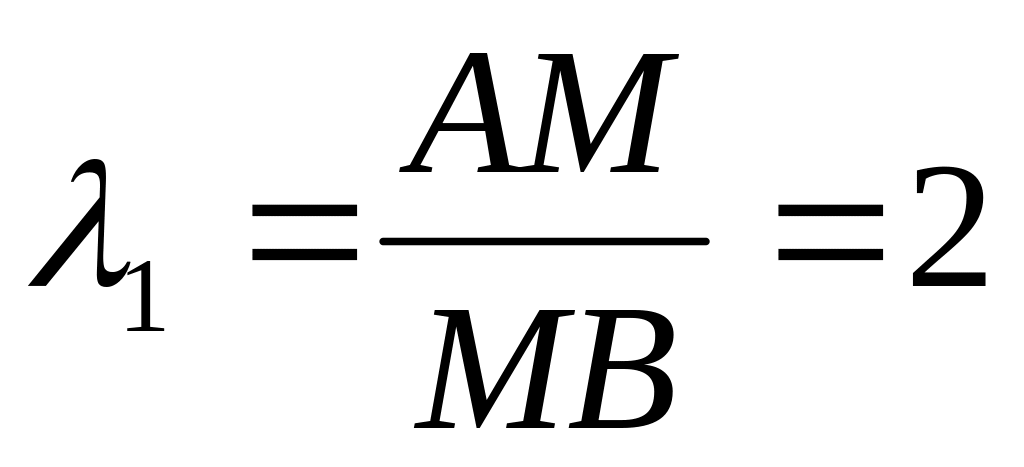, б) , в)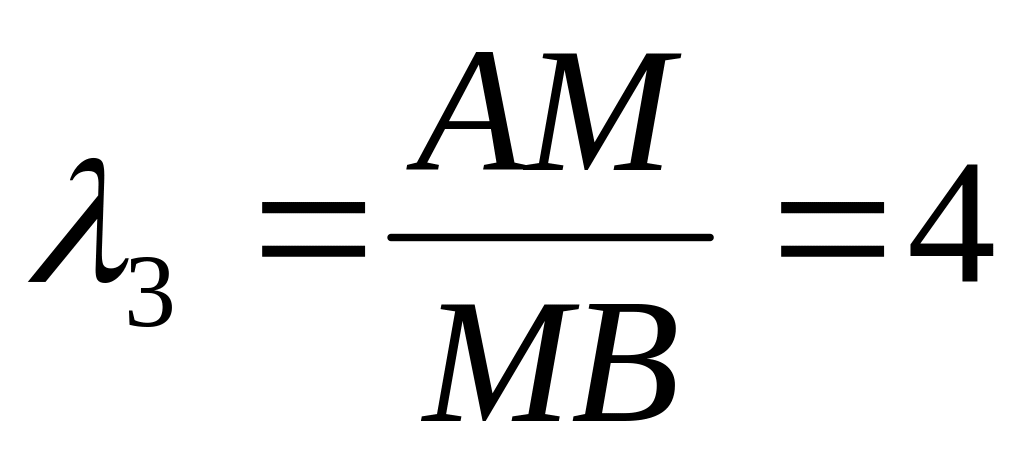 . Постройте точки.

5. Постройте в прямоугольной системе координат точки A(3; 5), B(–4;–2), D(–2;–2), E(–6; 0), K(0; 3).

6. Найдите расстояние между точками: а) A(–3;–5) и B(2; 7); б) A(2; 7) и B(6; 4).

7. Найдите координаты центра тяжести треугольника с вершинами А(3; 2), В(–1;–1), С(11;–6).

8. Вычислите длины сторон и площадь треугольника с вершинами А(3; 2), В(–1;–1), С(11;–6).

9. Докажите, что треугольник с вершинами О(0; 0), А(3; 1), В(1; 7) –прямоугольный.

10. Найдите координаты вершин квадрата, диагональ которого равна 6 см, точка пересечения диагоналей находится в начале координат, а диагонали лежат на осях координат.

12