Способы задания
1) , где векторы , – неколлинеарные.
2)
,
где две пересекающиеся направленные
прямые – оси,
точка пересечения прямых – начало
отсчета
– точка О,
и Е1,
Е2
–
единичные
точки,
говорят: в плоскости задана система
координат (репер – инженер.).
Точка
О
делит каждую ось на два луча: лучи с
положительным направлением, одинаково
направленные с векторами
,
и содержащие точки Е1,
Е2
соответственно, с отрицательным – не
содержащих эти точки (рис.1.7).
Координаты точки. Построение точки по ее координатам
П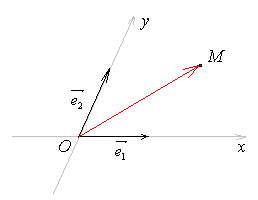
усть
дана аффинная система координат
.
Положение точки М
плоскости
полностью определяется
вектором
(рис.1.8), который единственным образом
раскладывается по
базисным векторам
и
.
(9)
Рис.1.8.
Из теоремы о разложении вектора плоскости по двум неколлинеарным векторам следует единственность коэффициентов х и у его разложения (9) по базисным векторам и . Таким образом, вектору соответствует единственная пара действительных чисел (х; у).
Определение 5
Вектор называется радиус-вектором точки М.
Определение 6
П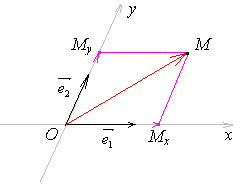
ара
чисел х,
у
называется координатами
точки М
в заданной системе координат и записывается
М(х;
у).
Соответствие
между точкой и радиус-вектором
взаимнооднозначное:
,
в том числе
.
Если М1М2,
то х1х2
и/или у1у2.
Пусть даны и М(х; у). Тогда по правилу параллелограмма (рис.1.9):
=
.
Е
Рис.1.9.
,
если у=0,
то
.
Для построения точки достаточно построить параллелограмм ОМхММу с диагональю ОМ.
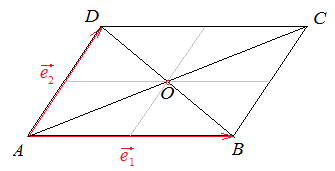
Пример 2.
Дано: параллелограмм ABCD, точка О – точка пересечения диагоналей.
Система координат
,
где
.
Н
Рис.1.10.
Решение.
Учитывая, что точка О делит диагонали параллелограмма пополам (рис.1.10):
,
отсюда
.
4. Аффинные задачи
Задача 5. Вычисление координат вектора
Д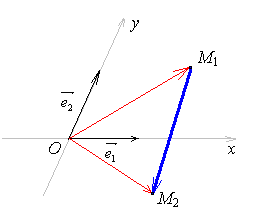
ано:
,
М1(х1;
у1),
М2(х2;
у2)
Найти:
координаты
.
Решение (рис.1.11):
,
т.е.
(10)
Рис.1.11.
Координаты вектора, заданного координатами его начала и конца в аффинной системе координат, равны разности одноименных координат точек – конца и начала вектора соответственно.
Задача 6. Деление отрезка в данном отношении
Дано: , М1(х1; у1), М2(х2; у2), R.
Найти: координаты точки М(х; у) / .
Решение.
Точка М
делит направленный отрезок
в отношении ,
т.е.
.
Для радиус-векторов точек справедливо
равенство
.
Откуда по аналогии с выводом формул
(5)-(7) и по свойству координат линейной
комбинации векторов получим:
или
(11)
Точка М принадлежит отрезку М1М2, если >0, и лежит вне отрезка М1М2, если <0. В первом случае будем говорить, что точка М делит отрезок М1М2 внутренним образом, во втором – внешним образом. Задача имеет решение при всех . Точка М – единственная для любых .
Для
точек, принадлежащих одной прямой,
(7) или
.
Пример 3.
Дано:
М1(6;
0), М2(–2;
1),
.
Найти:
координаты точки М(х;
у)
/
.
Р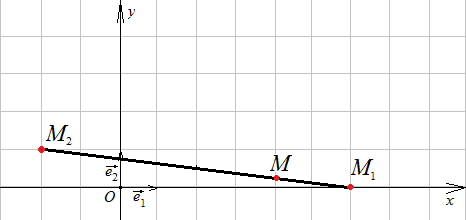
ешение.
.
.
П
Рис.1.12.
Если
,
то
,
.
Пример 4.
Дано: точки A(2; 1), B(6; 3), C(4; 2), D(8; 4), F(–4; –2) лежат на одной прямой.
,
,
Найти:
.
Решение.
Воспользуемся формулой (7):
,
,
.
,
,
.
Задача 7. Вычисление координат середины отрезка
Это частный случай формул (9): при . Тогда получим:
(12)
Координаты середины отрезка равны полусумме одноименных координат его концов.
Пример 5.
Дано: М1(6; 0), М2(–2; 1).
Найти: координаты точки Р(х; у) – середины отрезка М1М2.
Решение.
.
Тогда
.
Задача 8. Условие принадлежности трех точек одной прямой
Задача 9. Вычисление центра тяжести треугольника и многоугольника
(Задачи 8-9 самостоятельно)